4.4: Body Density from Displacement and Weight
( \newcommand{\kernel}{\mathrm{null}\,}\)
Mass from Weight
Scales measure weight, but to calculate body density we need mass. Some scales read off mass, such as the electronic scale in the image below, even though they actually measure weight.
A food product sits on a digital weighing scale with options for displaying weight in pounds or mass in kilograms or grams. The readout is 243 g. Image Credit: “Digi-keukenweegschaal1284” by Algont via wikimedia commons.
Mass can be determined from a weight because weight is just the force of gravity on the body and force of gravity depends on mass in a known way. On the surface of the Earth, the force gravity on an object is related to its mass by the equation:
(1)
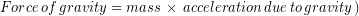
The acceleration due to gravity on Earth, typically abbreviated to g, has a value of 9.8 m/s2 and doesn’t change much over the entire surface of the Earth. Therefore we (and scales) can measure weight and then use equation (1) above to calculate mass. Understanding why the constant g is called the acceleration due to gravity requires introducing acceleration, which we will do in a later unit, so for now we recognize it as a constant value that relates mass and weight across the surface of Earth.
Reinforcement Exercise
In 2016 Helen Maroulis became the first American woman to win an Olympic gold medal in wrestling. She competes in the 53 kg class, which most people call her weight class. However, 53 kg is not actually a weight, it’s a mass. Use the formula provided above to calculate Helen’s weight in Newtons.
Find a conversion factor between Newtons and pounds and convert Helen’s competition weight to lbs.
Calculating Body Density
We now know how to measure volume by displacement and how to determine mass from a weight measurement so we should be able to determine body density. First we measure the weight, then calculate the mass. Dividing the mass by the volume found from our displacement measurement will give us the body density. Give it a try:
Reinforcement Exercises
A person weighs 902 N (203 lbs) What is the persons mass? (Assume they are on Earth’s surface)
The same person displaces 0.089 m3 of water volume when fully submerged. What is the body density of the person?
Body Weight and Mass on the Moon
The value of g only holds constant near the surface of the Earth, and therefore scales that equation (1) to calculate mass from measured weight will read incorrect results. For example, your mass doesn’t change just because you go to the moon (there isn’t suddenly less matter inside you), but your weight does change. In fact if you stood on a scale on the moon it would measure a weight about 1/6 of what it would read on Earth. The scale wouldn’t know you were on the moon instead of the Earth, so if the scale then tried to calculate your mass from weight, it would read a mass that is 1/6 the actual value. Of course you didn’t lose 5/6 of yourself on the way there, so that would not be correct.
Universal Law of Gravitation*
When you do want to calculate the force of gravity and you are not near the surface of the Earth then use the Universal Law of Gravitation.
The Universal Law of Gravitation states that the gravitational force between two objects depends on the mass of each object (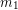 and
and 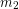 ) and the distance between their centers, (
) and the distance between their centers, ( ). To calculate the gravitational force we need to multiply the two masses together, divide by the distance between them squared, and finally multiply by the universal gravitational constant
). To calculate the gravitational force we need to multiply the two masses together, divide by the distance between them squared, and finally multiply by the universal gravitational constant 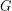 , which always has the same value of
, which always has the same value of 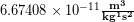 . Written in equation form the universal law of gravitation is:
. Written in equation form the universal law of gravitation is:
(2)
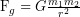
Reinforcement Exercise
Look up the mass and radius of the Earth and enter these into the Universal Law of Gravitation along with the value for 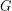 provided earlier. Use the mass of the Earth as
provided earlier. Use the mass of the Earth as 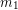 so
so 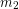 is the only thing left unknown in the equation. Multiply and divide everything other than
is the only thing left unknown in the equation. Multiply and divide everything other than 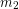 as indicated by the equation to get
as indicated by the equation to get 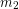 multiplied by a single number. What number did you find should be multiplied by an object’s mass to find the force of gravity? How does the resulting equation compare to the equation for the force of gravity near the surface of Earth that we stated earlier?
multiplied by a single number. What number did you find should be multiplied by an object’s mass to find the force of gravity? How does the resulting equation compare to the equation for the force of gravity near the surface of Earth that we stated earlier?
- "Digi-keukenweegschaal1284" by Algont [CC BY-SA 3.0 (http://creativecommons.org/licenses/by-sa/3.0/)] via wikimedia commons. ↵



