4.6: Hydrostatic Weighing
( \newcommand{\kernel}{\mathrm{null}\,}\)
 ) of a any object without any need for a volume (V) measurement by measuring only its weight (
) of a any object without any need for a volume (V) measurement by measuring only its weight ( ) and apparent weight, also known as under water weight (
) and apparent weight, also known as under water weight ( ). To see how we arrive at this useful result, follow the steps in the derivation at the end of this chapter.
). To see how we arrive at this useful result, follow the steps in the derivation at the end of this chapter.Reinforcement Exercises
Calculate the density of an that object that weighs 12 N, but has an apparent weight of only 8.5 N.
The previous equation is very similar to the body density equation used for hydrostatic weighing, but you will notice a slight difference. The previous equation determines the average density of the object including any hollow parts containing trapped air, but the body density equation is designed to determine the average density of body tissues only, not including trapped air. Therefore, the body density equation is modified to account for a volume of air trapped inside the body, known as the residual volume (RV). Also different standard symbols are used to designate body density, apparent weight, and water density.

Formulas used in calculating residual lung volume, body density, and body fat percentage. Image Credit: Measure Body Fat Via Under Water Weighing by MattVerlinich via Instructables
We arrived at equation (1) by starting with the definition of density as mass divided by its volume:
ρ=mOVO
We can find the mass of an object if we divide its weight by g:
m=WOg
Inserting that result for mass into the density equation we have:
ρ=WOgVO
For a completely submerged object the volume of water displaced is equal to the volume of the object, so we can replace 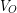 with
with 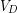 .
.
ρ=WOgVD
Using the definition of density again, we can replace the volume of water displaced with the displaced water mass (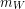 ) divided by water density (
) divided by water density (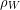 ).
).
\boldsymbol{\rho_W)} = \frac{W_O}{g m_D}\rho_W \end{equation*}}
 ), so we can make that substitution:
), so we can make that substitution:Archimedes' Principle which tells us that the buoyant forcepushing upward on objects in a fluid is equal to the weight displaced fluid. Therefore we can replace  with
with  .
.
ρ=WOFBρW
 ) and apparent weight (
) and apparent weight ( ) tells us the size of the buoyant force (
) tells us the size of the buoyant force ( ), as long as the body is in static equilibrium (holding still):
), as long as the body is in static equilibrium (holding still):Making that replacement in our density equation we have:
ρ=WOWO−FAρW
We now have an equation that allows us to calculate the density of an object by measuring only its weight and apparent weight, as long as we know the density of the fluid we are using.
Specific Gravity
The ratio of the density of a substance to that of water is known as the specific gravity. Specific gravity can be determined by hydrostatic weighing. If we simply divide both sides of our density equation by the density of water we will have a formula for the specific gravity:
SG=ρρW=WOWO−FA
Reinforcement Exercises
Calculate the specific gravity of an that object that weighs 12 N, but has an apparent weight of only 8.5 N.


