8.8: Quantitative Motion Analysis
( \newcommand{\kernel}{\mathrm{null}\,}\)
Calculating Position and Velocity
Based on our definition of acceleration as the rate of change of the velocity we can calculate the change in velocity during a time interval as the acceleration multiplied by the length of the time interval:
(1)
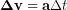
We can find the current velocity by adding the change in velocity to the initial velocity:
(2)
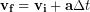
Using the definition of velocity as the rate of change of position we can calculate the change in position during a time interval as the average velocity during the interval multiplied by the length of the time interval.
(3)
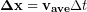
We can calculate the average velocity during the interval as the average of the initial and final velocities:
(4)
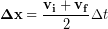
Finally using equation (2) we can replace the final velocity:
(5)
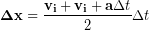
After some simplification:
(6)
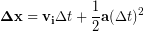
Adding the change in position to the initial position allows us to calculate the final position after any time:
(7)
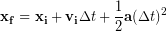
Reinforcement Exercises
A car accelerates from rest at 3 m/s/s. What is the car’s velocity after 5 s and how far does the car move in the first 5 s ? [Hint: The car starts from rest so the initial velocity is zero.]
Everyday Example
After leaving a friend’s 3rd story apartment you get to your car and realize that you have left your keys in the apartment. You call your friend and ask them to drop the keys out the window to you. We want to figure out how long it will take the keys to reach you and how fast they will be falling when they get there. The third story window is about 35 ft off the ground. We can convert to meters and use our previously stated acceleration for falling objects, g =9.8 m/s/s, or we can stick with feet and use g = 32 ft/s/s, so let’s do that.
Starting from our last equation from the work we did above:
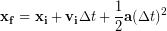
We choose upward as our positive direction and the ground as our origin, therefore our initial position is 35 ft and our final position is 0 ft. The keys are dropped from rest, so our initial velocity is zero. Putting the zeros into the equation above we have:
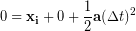
Now we can isolate the time variable:
(8)
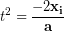
Take the square root to find the time
(9)
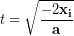
Entering our known values we can find the fall time. We will use -32 ft/s/s for our acceleration because the acceleration due to gravity is downward and we have chosen upward as the positive direction.
(10)
![]()
Lastly, we can find the velocity of the keys using equation (2) above
(11)
![]()
The final velocity of 47 ft/s is about 32 MPH. If the keys smack your hand at that speed, it will hurt. There are techniques you could use to prevent injury in such a situation, and those techniques will be the topic of the next Unit.
The Jerk
We have learned in the last few chapters that our example skydiver has an initial acceleration of 9.8 m/s/s and an acceleration of zero after reaching terminal velocity, so between those points the acceleration must be changing. The rate of change of the acceleration is known as the jerk, but we won’t deal with jerk in this textbook and will instead focus on motion with constant acceleration. However, if we really want to analyze our skydiver’s full motion, we will need to somehow deal with a changing acceleration. That’s what the next chapter is all about.


