8.5: Analyzing Skydiving Motion
- Page ID
- 17771
Vertical Position During a Skydive
When analyzing the fall of a skydiver we need to consider that the skydiver is changing position all the time, so they must have a speed. If we know the direction along with the speed, then we know the velocity. We also know that they eventually reach a terminal speed, but before that point the are speeding up, which means they are accelerating. We will apply these same three important concepts in analyzing the motion of any object:
- Position
- Velocity
- Acceleration
Position
Position describes the location of an object according to a choice of zero point and positive direction. The zero point is called the origin and upwards is commonly used as the positive direction when analyzing vertical motion. For example, with upward positive, a skydiver in a stationary balloon at an altitude of 12,000 ft would have a position of 12,000 ft, if we called the ground the origin. If we chose 12000 ft as the origin then the position of the skydiver would be zero. If we chose 24,000 ft as the origin, the skydiver would have a position of -12,000 ft. It doesn’t matter where you put the origin or which direction is positive as long as you keep them both consistent throughout your analysis.
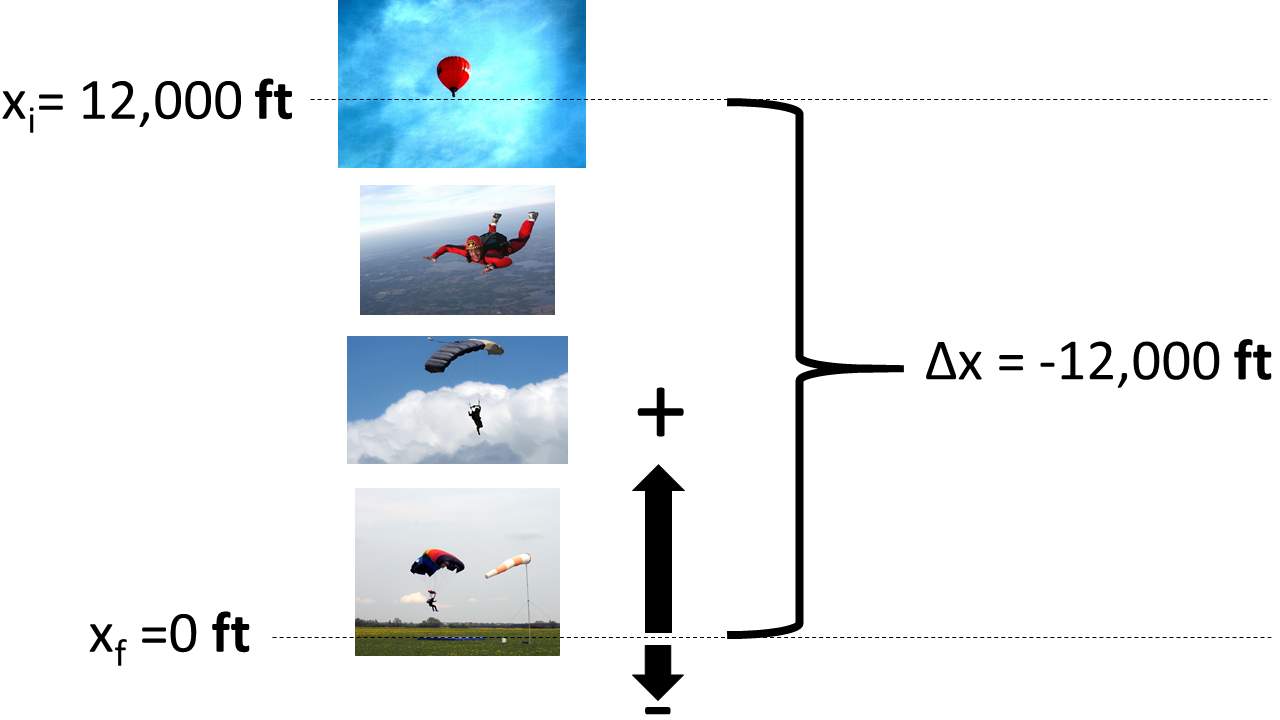
Initial position, final position, and displacement of a skydiver from jump to landing. Ground level was chosen as the origin and upwards as the positive direction. Image adapted from Balloon over Straubing, Germany by Runologe, “Gabriel Skydiving” By Gabriel Christian Brown, “EOD parachute jump” Petty Officer 3rd Class Daniel Rolstonvia and Parachute precise landing by Masur, all via Wikimedia Commons
Let’s say we placed the origin at the ground and chose upwards as positive, as in the diagram above. If we are analyzing the motion of the skydiver starting just as they jump to just as they land, then their initial position (xi) would 12,000 ft and their final position (xf)would be 0 ft. The change in position would be -12,000 ft because they moved 12,000 ft downward, which is the negative direction. We call the change in position the displacement (Δx) and we calculate the displacement as:
(1)
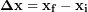
For our skydiver example we have:
(2)
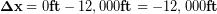
Vectors
As we analyze motion we are beginning to see that it is very important to keep track of directions for different quantities, like position and displacement. We also know that forces and torques have directions and we have accounted for that by adding or subtracting forces based on the directions they point in our free body diagrams. However, as we introduce new quantities we will need to remember which quantities require keeping track of their direction (vectors) and which don’t (scalars). We will make the symbols for vectors bold when writing equations. We should be able to avoid confusion with our bold units by only writing units behind numeric values and not behind symbols. Notice we have already started using this bold convention in this chapter for our position and displacement symbols.
Distance
It may seem odd that we have introduced displacement as a new word for distance that something travels, but there is actually an important distinction between the two terms. The distance and displacement are sometimes equal, but not always. For example, the distance our skydiver traveled from balloon to ground was 12,000 ft, but their displacement was -12,000 ft. If we analyze the motion of the skydiver starting from when they got into the balloon on the ground to when they landed after the jump then the distance traveled by the skydiver would be 24,000 ft. However, the displacement would be 0 ft because their initial and final positions were the same. The distance traveled can be greater than, or equal to the displacement, but it can never be less. This distinction arises because direction matters in calculating displacement, but not in measuring distance.
Reinforcement Exercise
You throw a ball 3 m into the air and it returns to your hand. What are the displacement of the ball and distance traveled by the ball for:
- The first half of the ball’s trip (from your hand to the ball’s peak height).
- The second half of the ball’s trip (from peak height back to your hand).
- The entire round trip of the ball.
Velocity during a Skydive
Instantaneous Speed and Velocity
The maximum speed reached by a body (or any object) falling under the influence of both gravitational force and air resistance is often called terminal velocity or terminal speed. In everyday life we often use speed and velocity to mean the same thing, but they actually have different meanings in physics. Velocity is the rate at which the position is changing and speed is the rate at which distance is covered. Objects cannot travel negative distances so the speed will always be positive. However, position can become more negative, as was the case for our example skydiver, so velocity can be negative. The speed at any instant in time is known as the instantaneous speed. The instantaneous velocity is just the instantaneous speed with a direction included. For example, if at some point our skydiver reached a terminal speed of 89 MPH, then their terminal velocity would be 89 MPHdownward or -89 MPH for our choice of downward as the negative direction.
Initial and Final Velocity
Just as we defined initial position and final position for the section of an object’s motion that we are analyzing, we can also define initial velocity and final velocity. For example, if we analyze the skydiver’s motion from jump until they reach an example terminal speed of 180 MPH, then the initial velocity of our skydiver was zero and the final velocity was -180 MPH.
Average Velocity
Sometimes we are interested in the average velocity over some amount of time rather than the instantaneous velocity at a single time. To calculate the average velocity for a section of an objects motion we need to divide the change in position (displacement) by the time interval (Δt) over which the it occurred.
(3)
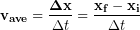
Velocities will be negative when the displacement is negative, as was the case for our skydiver’s trip from balloon to ground. The negative displacement of our skydiver would result in a negative average velocity during their trip from balloon to ground. This makes sense, as we should be expecting a negative velocity for our skydiver because downward was chosen as our negative direction and the skydiver was moving downward.
Average Speed
Sometimes average speed and average velocity are the same, but sometimes they are not. Speed is the rate at which distance is traveled so to calculate average speed we divide the distance traveled by the time required for the travel. Remembering that we use displacement rather than distance in calculating average velocity, we can see that speed and velocity are different. For example the velocity of the skydiver in our example is negative on the way down because displacement is negative, however we cannot say the diver actually traveled a negative distance, so the average speed is positive.
Everyday Examples
Let’s imagine the skydiver in our example rode a hot air balloon upward for 21 minutes, then jumped and fell for 2.0 minutes, then opened their parachute and drifted downward for 5.0 minutes before landing. Let’s calculate the average speed and average velocity for the entire trip in feet per minute.
The average speed is the total distance covered divided by the total time, which would be 24,000 ft divided by 27 minutes for a speed of: 860 ft/min.
The average velocity would be the total displacement divided by the total time. The skydiver started and ended the trip on the ground, so the total displacement for the round trip was zero, therefore the average velocity for the trip was zero! Comparing this average velocity to the average speed of 860 ft/min we can really see why distinguishing between instantaneous or average and speed or velocity is important.
Reinforcement Activities
If the parachute of the skydiver in the previous everyday example opened at 2900 ft, what would be their average speed during the remaining 5.0 minutes it took to hit the ground? What would be their average velocity?
- Balloon over Straubing, Germany by Runologe, via wikimedia commons↵
- "Gabriel Skydiving" By Gabriel Christian Brown [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], from Wikimedia Commons↵
- "EOD parachute jump" Petty Officer 3rd Class Daniel Rolston (https://www.dvidshub.net/image/1465626) [Public domain], via Wikimedia Commons↵
- Parachute precise landing by Masur [Public domain], via Wikimedia Commons↵


