4.E: Problems
- Page ID
- 1005
1. Derive a formula expressing the kinetic energy of an object in terms of its momentum and mass.(answer check available at lightandmatter.com)
2. Two people in a rowboat wish to move around without causing the boat to move. What should be true about their total momentum? Explain.
3. A bullet leaves the barrel of a gun with a kinetic energy of 90 J. The gun barrel is 50 cm long. The gun has a mass of 4 kg, the bullet 10 g.
(a) Find the bullet's final velocity. (answer check available at lightandmatter.com)
(b) Find the bullet's final momentum. (answer check available at lightandmatter.com)
(c) Find the momentum of the recoiling gun.
(d) Find the kinetic energy of the recoiling gun, and explain why the recoiling gun does not kill the shooter. (answer check available at lightandmatter.com)
4. (solution in the pdf version of the book) The big difference between the equations for momentum and kinetic energy is that one is proportional to \(v\) and one to \(v^2\). Both, however, are proportional to \(m\). Suppose someone tells you that there's a third quantity, funkosity, defined as \(f=m^2v\), and that funkosity is conserved. How do you know your leg is being pulled?
5. A ball of mass \(2m\) collides head-on with an initially stationary ball of mass \(m\). No kinetic energy is transformed into heat or sound. In what direction is the mass-\(2m\) ball moving after the collision, and how fast is it going compared to its original velocity? \hwans{hwans:twotoonecollision}
6. A very massive object with velocity \(v\) collides head-on with an object at rest whose mass is very small. No kinetic energy is converted into other forms. Prove that the low-mass object recoils with velocity \(2v\). [Hint: Use the center-of-mass frame of reference.]
7. A mass \(m\) moving at velocity \(v\) collides with a stationary target having the same mass \(m\). Find the maximum amount of energy that can be released as heat and sound. (answer check available at lightandmatter.com)
8. A rocket ejects exhaust with an exhaust velocity \(u\). The rate at which the exhaust mass is used (mass per unit time) is \(b\). We assume that the rocket accelerates in a straight line starting from rest, and that no external forces act on it. Let the rocket's initial mass (fuel plus the body and payload) be \(m_i\), and \(m_f\) be its final mass, after all the fuel is used up. (a) Find the rocket's final velocity, \(v\), in terms of \(u\), \(m_i\), and \(m_f\). Neglect the effects of special relativity. (b) A typical exhaust velocity for chemical rocket engines is 4000 m/s. Estimate the initial mass of a rocket that could accelerate a one-ton payload to 10% of the speed of light, and show that this design won't work. (For the sake of the estimate, ignore the mass of the fuel tanks. The speed is fairly small compared to \(c\), so it's not an unreasonable approximation to ignore relativity.) (answer check available at lightandmatter.com)
9. An object is observed to be moving at constant speed along a line. Can you conclude that no forces are acting on it? Explain. [Based on a problem by Serway and Faughn.]
10. At low speeds, every car's acceleration is limited by traction, not by the engine's power. Suppose that at low speeds, a certain car is normally capable of an acceleration of \(3\ \text{m}/\text{s}^2\). If it is towing a trailer with half as much mass as the car itself, what acceleration can it achieve? [Based on a problem from PSSC Physics.]
11. (a) Let \(T\) be the maximum tension that an elevator's cable can withstand without breaking, i.e., the maximum force it can exert. If the motor is programmed to give the car an acceleration \(a\) (\(a>0\) is upward), what is the maximum mass that the car can have, including passengers, if the cable is not to break?(answer check available at lightandmatter.com)
(b) Interpret the equation you derived in the special cases of \(a=0\) and of a downward acceleration of magnitude \(g\).
12. (solution in the pdf version of the book) When the contents of a refrigerator cool down, the changed molecular speeds imply changes in both momentum and energy. Why, then, does a fridge transfer power through its radiator coils, but not force?
13. A helicopter of mass \(m\) is taking off vertically. The only forces acting on it are the earth's gravitational force and the force, \(F_{air}\), of the air pushing up on the propeller blades.
(a) If the helicopter lifts off at \(t=0\), what is its vertical speed at time \(t\)?
(b) Check that the units of your answer to part a make sense.
(c) Discuss how your answer to part a depends on all three variables, and show that it makes sense. That is, for each variable, discuss what would happen to the result if you changed it while keeping the other two variables constant. Would a bigger value give a smaller result, or a bigger result? Once you've figured out this mathematical relationship, show that it makes sense physically.
(d) Plug numbers into your equation from part a, using \(m=2300\) kg, \(F_{air}=27000\ \text{N}\), and \(t=4.0\ \text{s}\). (answer check available at lightandmatter.com)
14. A blimp is initially at rest, hovering, when at \(t=0\) the pilot turns on the motor of the propeller. The motor cannot instantly get the propeller going, but the propeller speeds up steadily. The steadily increasing force between the air and the propeller is given by the equation \(F=kt\), where \(k\) is a constant. If the mass of the blimp is \(m\), find its position as a function of time. (Assume that during the period of time you're dealing with, the blimp is not yet moving fast enough to cause a significant backward force due to air resistance.)(answer check available at lightandmatter.com)
15. (solution in the pdf version of the book) A car is accelerating forward along a straight road. If the force of the road on the car's wheels, pushing it forward, is a constant 3.0 kN, and the car's mass is 1000 kg, then how long will the car take to go from 20 m/s to 50 m/s?
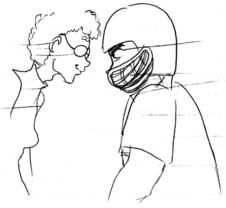
a / Problem 16.
16. A little old lady and a pro football player collide head-on. Compare their forces on each other, and compare their accelerations. Explain.
17. The earth is attracted to an object with a force equal and opposite to the force of the earth on the object. If this is true, why is it that when you drop an object, the earth does not have an acceleration equal and opposite to that of the object?
18. When you stand still, there are two forces acting on you, the force of gravity (your weight) and the normal force of the floor pushing up on your feet. Are these forces equal and opposite? Does Newton's third law relate them to each other? Explain.
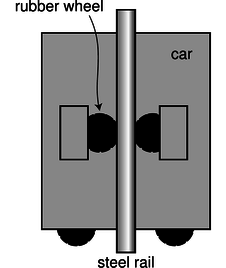
b / Problem 19.
19. Today's tallest buildings are really not that much taller than the tallest buildings of the 1940's. One big problem with making an even taller skyscraper is that every elevator needs its own shaft running the whole height of the building. So many elevators are needed to serve the building's thousands of occupants that the elevator shafts start taking up too much of the space within the building. An alternative is to have elevators that can move both horizontally and vertically: with such a design, many elevator cars can share a few shafts, and they don't get in each other's way too much because they can detour around each other. In this design, it becomes impossible to hang the cars from cables, so they would instead have to ride on rails which they grab onto with wheels. Friction would keep them from slipping. The figure shows such a frictional elevator in its vertical travel mode. (The wheels on the bottom are for when it needs to switch to horizontal motion.)
(a) If the coefficient of static friction between rubber and steel is \(\mu_s\), and the maximum mass of the car plus its passengers is \(M\), how much force must there be pressing each wheel against the rail in order to keep the car from slipping? (Assume the car is not accelerating.)(answer check available at lightandmatter.com)
(b) Show that your result has physically reasonable behavior with respect to \(\mu_s\). In other words, if there was less friction, would the wheels need to be pressed more firmly or less firmly? Does your equation behave that way?
20. A tugboat of mass \(m\) pulls a ship of mass \(M\), accelerating it. Ignore fluid friction acting on their hulls, although there will of course need to be fluid friction acting on the tug's propellers.
(a) If the force acting on the tug's propeller is \(F\), what is the tension, \(T\), in the cable connecting the two ships? \hwhint{hwhint:tugboat}(answer check available at lightandmatter.com)
(b) Interpret your answer in the special cases of \(M=0\) and \(M=\infty\).
21. Someone tells you she knows of a certain type of Central American earthworm whose skin, when rubbed on polished diamond, has \(\mu_k>\mu_s\). Why is this not just empirically unlikely but logically suspect?
22. A uranium atom deep in the earth spits out an alpha particle. An alpha particle is a fragment of an atom. This alpha particle has initial speed \(v\), and travels a distance \(d\) before stopping in the earth.
(a) Find the force, \(F\), from the dirt that stopped the particle, in terms of \(v,d\), and its mass, \(m\). Don't plug in any numbers yet. Assume that the force was constant.(answer check available at lightandmatter.com)
(b) Show that your answer has the right units.
(c) Discuss how your answer to part a depends on all three variables, and show that it makes sense. That is, for each variable, discuss what would happen to the result if you changed it while keeping the other two variables constant. Would a bigger value give a smaller result, or a bigger result? Once you've figured out this mathematical relationship, show that it makes sense physically.
(d) Evaluate your result for \(m=6.7\times10^{-27}\) kg, \(v=2.0\times10^4\) km/s, and \(d=0.71\) mm.(answer check available at lightandmatter.com)

c / Problem 23, part c.
23. You are given a large sealed box, and are not allowed to open it. Which of the following experiments measure its mass, and which measure its weight? [Hint: Which experiments would give different results on the moon?]
(a) Put it on a frozen lake, throw a rock at it, and see how fast it scoots away after being hit.
(b) Drop it from a third-floor balcony, and measure how loud the sound is when it hits the ground.
(c) As shown in the figure, connect it with a spring to the wall, and watch it vibrate.
(solution in the pdf version of the book)
24. While escaping from the palace of the evil Martian emperor, Sally Spacehound jumps from a tower of height \(h\) down to the ground. Ordinarily the fall would be fatal, but she fires her blaster rifle straight down, producing an upward force of magnitude \(F_B\). This force is insufficient to levitate her, but it does cancel out some of the force of gravity. During the time \(t\) that she is falling, Sally is unfortunately exposed to fire from the emperor's minions, and can't dodge their shots. Let \(m\) be her mass, and \(g\) the strength of gravity on Mars.
(a) Find the time \(t\) in terms of the other variables.
(b) Check the units of your answer to part a.
(c) For sufficiently large values of \(F_B\), your answer to part a becomes nonsense --- explain what's going on.(answer check available at lightandmatter.com)
25. When I cook rice, some of the dry grains always stick to the measuring cup. To get them out, I turn the measuring cup upside-down and hit the “roof” with my hand so that the grains come off of the “ceiling.” (a) Explain why static friction is irrelevant here. (b) Explain why gravity is negligible. (c) Explain why hitting the cup works, and why its success depends on hitting the cup hard enough.
26. A flexible rope of mass \(m\) and length \(L\) slides without friction over the edge of a table. Let \(x\) be the length of the rope that is hanging over the edge at a given moment in time.
(a) Show that \(x\) satisfies the equation of motion \(d^2x/dt^2=gx/L\). [Hint: Use \(F=dp/dt\), which allows you to handle the two parts of the rope separately even though mass is moving out of one part and into the other.]
(b) Give a physical explanation for the fact that a larger value of \(x\) on the right-hand side of the equation leads to a greater value of the acceleration on the left side.
(c) When we take the second derivative of the function \(x(t)\) we are supposed to get essentially the same function back again, except for a constant out in front. The function \(e^x\) has the property that it is unchanged by differentiation, so it is reasonable to look for solutions to this problem that are of the form \(x=be^{ct}\), where \(b\) and \(c\) are constants. Show that this does indeed provide a solution for two specific values of \(c\) (and for any value of \(b)\).
(d) Show that the sum of any two solutions to the equation of motion is also a solution.
(e) Find the solution for the case where the rope starts at rest at \(t=0\) with some nonzero value of \(x\).
In problems 27-31, analyze the forces using a table in the format shown in section 3.2.6. Analyze the forces in which the italicized object participates.
27. Some people put a spare car key in a little magnetic box that they stick under the chassis of their car. Let's say that the box is stuck directly underneath a horizontal surface, and the car is parked. (See instructions above.)
28. Analyze two examples of objects at rest relative to the earth that are being kept from falling by forces other than the normal force. Do not use objects in outer space, and do not duplicate problem 27 or 31. (See instructions above.)
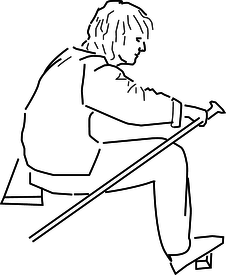
d / Problem 29.
29. A person is rowing a boat, with her feet braced. She is doing the part of the stroke that propels the boat, with the ends of the oars in the water (not the part where the oars are out of the water). (See instructions above.)
30. A farmer is in a stall with a cow when the cow decides to press him against the wall, pinning him with his feet off the ground. Analyze the forces in which the farmer participates. (See instructions above.)
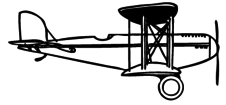
e / Problem 31.
31. A propeller plane is cruising east at constant speed and altitude. (See instructions above.)
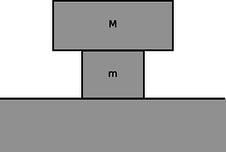
f / Problem 32
32. The figure shows a stack of two blocks, sitting on top of a table that is bolted to the floor. All three objects are made from identical wood, with their surfaces finished identically using the same sandpaper. We tap the middle block, giving it an initial velocity \(v\) to the right. The tap is executed so rapidly that almost no initial velocity is imparted to the top block.
(a) Find the time that will elapse until the slipping between the top and middle blocks stops. Express your answer in terms of \(v\), \(m\), \(M\), \(g\), and the relevant coefficient of friction.(answer check available at lightandmatter.com)
(b) Show that your answer makes sense in terms of units.
(c) Check that your result has the correct behavior when you make \(m\) bigger or smaller. Explain. This means that you should discuss the mathematical behavior of the result, and then explain how this corresponds to what would really happen physically.
(d) Similarly, discuss what happens when you make \(M\) bigger or smaller.
(e) Similarly, discuss what happens when you make \(g\) bigger or smaller.
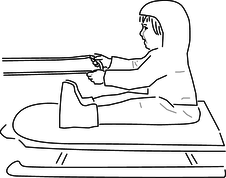
g / Problem 33.
33. Ginny has a plan. She is going to ride her sled while her dog Foo pulls her, and she holds on to his leash. However, Ginny hasn't taken physics, so there may be a problem: she may slide right off the sled when Foo starts pulling.
(a) Analyze all the forces in which Ginny participates, making a table as in subsection 3.2.6.
(b) Analyze all the forces in which the sled participates.
(c) The sled has mass \(m\), and Ginny has mass \(M\). The coefficient of static friction between the sled and the snow is \(\mu_1\), and \(\mu_2\) is the corresponding quantity for static friction between the sled and her snow pants. Ginny must have a certain minimum mass so that she will not slip off the sled. Find this in terms of the other three variables.(answer check available at lightandmatter.com)
(d) Interpreting your equation from part c, under what conditions will there be no physically realistic solution for \(M\)? Discuss what this means physically.
34. (solution in the pdf version of the book) In each case, identify the force that causes the acceleration, and give its Newton's-third-law partner. Describe the effect of the partner force. (a) A swimmer speeds up. (b) A golfer hits the ball off of the tee. (c) An archer fires an arrow. (d) A locomotive slows down.
35. A cop investigating the scene of an accident measures the length \(L\) of a car's skid marks in order to find out its speed \(v\) at the beginning of the skid. Express \(v\) in terms of \(L\) and any other relevant variables.(answer check available at lightandmatter.com)
36. An ice skater builds up some speed, and then coasts across the ice passively in a straight line. (a) Analyze the forces, using a table the format shown in subsection 3.2.6.
(b) If his initial speed is \(v\), and the coefficient of kinetic friction is \(\mu_k\), find the maximum theoretical distance he can glide before coming to a stop. Ignore air resistance.(answer check available at lightandmatter.com)
(c) Show that your answer to part b has the right units.
(d) Show that your answer to part b depends on the variables in a way that makes sense physically.
(e) Evaluate your answer numerically for \(\mu_k=0.0046\), and a world-record speed of \(14.58\) m/s. (The coefficient of friction was measured by De Koning et al., using special skates worn by real speed skaters.)(answer check available at lightandmatter.com)
(f) Comment on whether your answer in part e seems realistic. If it doesn't, suggest possible reasons why.
37. (a) Using the solution of problem 37 on page 124, predict how the spring constant of a fiber will depend on its length and cross-sectional area.
(b) The constant of proportionality is called the Young's modulus, \(E\), and typical values of the Young's modulus are about \(10^{10}\) to \(10^{11}\). What units would the Young's modulus have in the SI system? (solution in the pdf version of the book)
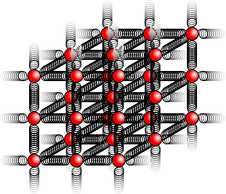
h / Problem 38
38. This problem depends on the results of problems problem 37 on page 124 and problem 37 from this chapter. When atoms form chemical bonds, it makes sense to talk about the spring constant of the bond as a measure of how “stiff” it is. Of course, there aren't really little springs --- this is just a mechanical model. The purpose of this problem is to estimate the spring constant, \(k\), for a single bond in a typical piece of solid matter. Suppose we have a fiber, like a hair or a piece of fishing line, and imagine for simplicity that it is made of atoms of a single element stacked in a cubical manner, as shown in the figure, with a center-to-center spacing \(b\). A typical value for \(b\) would be about \(10^{-10}\ \text{m}\).
(a) Find an equation for \(k\) in terms of \(b\), and in terms of the Young's modulus, \(E\), defined in problem 37 and its solution.
(b) Estimate \(k\) using the numerical data given in problem 37.
(c) Suppose you could grab one of the atoms in a diatomic molecule like \(\text{H}_2\) or \(\text{O}_2\), and let the other atom hang vertically below it. Does the bond stretch by any appreciable fraction due to gravity?
39. This problem has been deleted.
40. Many fish have an organ known as a swim bladder, an air-filled cavity whose main purpose is to control the fish's buoyancy an allow it to keep from rising or sinking without having to use its muscles. In some fish, however, the swim bladder (or a small extension of it) is linked to the ear and serves the additional purpose of amplifying sound waves. For a typical fish having such an anatomy, the bladder has a resonant frequency of 300 Hz, the bladder's \(Q\) is 3, and the maximum amplification is about a factor of 100 in energy. Over what range of frequencies would the amplification be at least a factor of 50?
41. An oscillator with sufficiently strong damping has its maximum response at \(\omega=0\). Using the result derived on page 912 , find the value of \(Q\) at which this behavior sets in. \hwhint{hwhint:maxampatdc}\hwans{hwans:maxampatdc}
42. An oscillator has \(Q\)=6.00, and, for convenience, let's assume \(F_m=1.00\), \(\omega_\text{o}=1.00\), and \(m=1.00\). The usual approximations would give
Determine these three quantities numerically using the result derived on page 912 , and compare with the approximations.
43. The apparatus in figure d on page 61 had a natural period of oscillation of 5 hours and 20 minutes. The authors estimated, based on calculations of internal friction in the tungsten wire, that its \(Q\) was on the order of \(10^6\), but they were unable to measure it empirically because it would have taken years for the amplitude to die down by any measurable amount. Although each aluminum or platinum mass was really moving along an arc of a circle, any actual oscillations caused by a violation of the equivalence of gravitational and inertial mass would have been measured in millions of a degree, so it's a good approximation to say that each mass's motion was along a (very short!) straight line segment. We can also treat each mass as if it was oscillating separately from the others. If the principle of equivalence had been violated at the \(10^{-12}\) level, the limit of their experiment's sensitivity, the sun's gravitational force on one of the 0.4-gram masses would have been about \(3\times10^{-19}\) N, oscillating with a period of 24 hours due to the rotation of the earth. (We ignore the inertia of the arms, whose total mass was only about 25% of the total mass of the rotating assembly.)
(a) Find the amplitude of the resulting oscillations, and determine the angle to which they would have corresponded, given that the radius of the balance arms was 10 cm.\hwans{hwans:braginskii}
(b) Show that even if their estimate of \(Q\) was wildly wrong, it wouldn't have affected this result.
44. (solution in the pdf version of the book) A firework shoots up into the air, and just before it explodes it has a certain momentum and kinetic energy. What can you say about the momenta and kinetic energies of the pieces immediately after the explosion? [Based on a problem from PSSC Physics.]
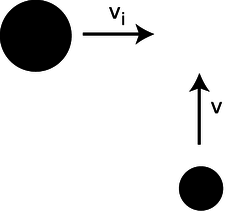
i / Problem 45
45. (solution in the pdf version of the book) The figure shows a view from above of a collision about to happen between two air hockey pucks sliding without friction. They have the same speed, \(v_i\), before the collision, but the big puck is 2.3 times more massive than the small one. Their sides have sticky stuff on them, so when they collide, they will stick together. At what angle will they emerge from the collision? In addition to giving a numerical answer, please indicate by drawing on the figure how your angle is defined.
46. A learjet traveling due east at 300 mi/hr collides with a jumbo jet which was heading southwest at 150 mi/hr. The jumbo jet's mass is five times greater than that of the learjet. When they collide, the learjet sticks into the fuselage of the jumbo jet, and they fall to earth together. Their engines stop functioning immediately after the collision. On a map, what will be the direction from the location of the collision to the place where the wreckage hits the ground? (Give an angle.)(answer check available at lightandmatter.com)
47. (a) A ball is thrown straight up with velocity \(v\). Find an equation for the height to which it rises.(answer check available at lightandmatter.com)
(b) Generalize your equation for a ball thrown at an angle \(\theta \) above horizontal, in which case its initial velocity components are \(v_x=v \cos \theta \) and \(v_y=v \sin \theta \).(answer check available at lightandmatter.com)
48. At the 2010 Salinas Lettuce Festival Parade, the Lettuce Queen drops her bouquet while riding on a float moving toward the right. Sketch the shape of its trajectory in her frame of reference, and compare with the shape seen by one of her admirers standing on the sidewalk.
49. Two daredevils, Wendy and Bill, go over Niagara Falls. Wendy sits in an inner tube, and lets the 30 km/hr velocity of the river throw her out horizontally over the falls. Bill paddles a kayak, adding an extra 10 km/hr to his velocity. They go over the edge of the falls at the same moment, side by side. Ignore air friction. Explain your reasoning.
(a) Who hits the bottom first?
(b) What is the horizontal component of Wendy's velocity on impact?
(c) What is the horizontal component of Bill's velocity on impact?
(d) Who is going faster on impact?
50. A baseball pitcher throws a pitch clocked at \(v_x\)=73.3 mi/h. He throws horizontally. By what amount, \(d\), does the ball drop by the time it reaches home plate, \(L\)=60.0 ft away?
(a) First find a symbolic answer in terms of \(L\), \(v_x\), and \(g\).(answer check available at lightandmatter.com)
(b) Plug in and find a numerical answer. Express your answer in units of ft. (Note: 1 ft=12 in, 1 mi=5280 ft, and 1 in=2.54 cm) (answer check available at lightandmatter.com)
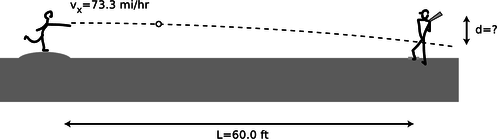
j / Problem 50.
51. A batter hits a baseball at speed \(v\), at an angle \(\theta\) above horizontal.
(a) Find an equation for the range (horizontal distance to where the ball falls), \(R\), in terms of the relevant variables. Neglect air friction and the height of the ball above the ground when it is hit. \hwans{hwans:baseballrange}
(b) Interpret your equation in the cases of \(\theta\)=0 and \(\theta=90°\).
(c) Find the angle that gives the maximum range.\hwans{hwans:baseballrange}
52. In this problem you'll extend the analysis in problem 51
to include air friction by writing a computer program. For a game played at sea level, the force due to air friction is approximately \((7\times10^{-4}\ \text{N}\!\cdot\!\text{s}^2/\text{m}^2)v^2\), in the direction opposite to the motion of the ball.The mass of a baseball is 0.146 kg.
(a) For a ball hit at a speed of 45.0 m/s from a height of 1.0 m, find the optimal angle and the resulting range. \hwans{hwans:baseballrangeair}
(b) How much farther would the ball fly at the Colorado Rockies' stadium, where the thinner air gives 18 percent less air friction? \hwans{hwans:baseballrangeair}
53. If you walk 35 km at an angle 25° counterclockwise from east, and then 22 km at 230° counterclockwise from east, find the distance and direction from your starting point to your destination. (answer check available at lightandmatter.com)
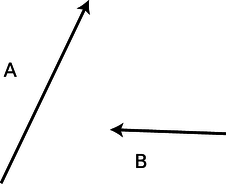
k / Problem 54.
54. The figure shows vectors \(\mathbf{A}\) and \(\mathbf{B}\). As in figure p on p. 200, graphically calculate the following:
\(\mathbf{A}+\mathbf{B}\), \(\mathbf{A}-\mathbf{B}\), \(\mathbf{B}-\mathbf{A}\), \(-2\mathbf{B}\), \(\mathbf{A}-2\mathbf{B}\)
No numbers are involved.
55. Phnom Penh is 470 km east and 250 km south of Bangkok. Hanoi is 60 km east and 1030 km north of Phnom Penh.
(a) Choose a coordinate system, and translate these data into \(\Delta x\) and \(\Delta y\) values with the proper plus and minus signs.
(b) Find the components of the \(\Delta \mathbf{r}\) vector pointing from Bangkok to Hanoi.(answer check available at lightandmatter.com)
56. Is it possible for a helicopter to have an acceleration due east and a velocity due west? If so, what would be going on? If not, why not?
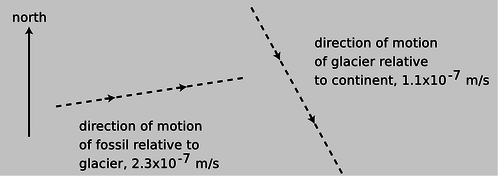
l / Problem 57.
57. A dinosaur fossil is slowly moving down the slope of a glacier under the influence of wind, rain and gravity. At the same time, the glacier is moving relative to the continent underneath. The dashed lines represent the directions but not the magnitudes of the velocities. Pick a scale, and use graphical addition of vectors to find the magnitude and the direction of the fossil's velocity relative to the continent. You will need a ruler and protractor. (answer check available at lightandmatter.com)
58. A bird is initially flying horizontally east at 21.1 m/s, but one second later it has changed direction so that it is flying horizontally and \(7°\) north of east, at the same speed. What are the magnitude and direction of its acceleration vector during that one second time interval? (Assume its acceleration was roughly constant.) (answer check available at lightandmatter.com)
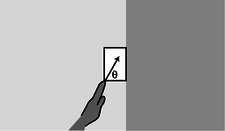
m / Problem 59
59. Your hand presses a block of mass \(m\) against a wall with a force \(\mathbf{F}_H\) acting at an angle \(\theta \), as shown in the figure. Find the minimum and maximum possible values of \(|\mathbf{F}_H|\) that can keep the block stationary, in terms of \(m\), \(g\), \(\theta\), and \(\mu_s\), the coefficient of static friction between the block and the wall. Check both your answers in the case of \(\theta=90°\), and interpret the case where the maximum force is infinite.(answer check available at lightandmatter.com)
60. A skier of mass \(m\) is coasting down a slope inclined at an angle \(\theta \) compared to horizontal. Assume for simplicity that the treatment of kinetic friction given in chapter 5 is appropriate here, although a soft and wet surface actually behaves a little differently. The coefficient of kinetic friction acting between the skis and the snow is \(\mu_k\), and in addition the skier experiences an air friction force of magnitude \(bv^2\), where \(b\) is a constant.
(a) Find the maximum speed that the skier will attain, in terms of the variables \(m\), \(g\), \(\theta\), \(\mu_k\), and \(b\).(answer check available at lightandmatter.com)
(b) For angles below a certain minimum angle \(\theta_{min}\), the equation gives a result that is not mathematically meaningful. Find an equation for \(\theta_{min}\), and give a physical explanation of what is happening for \(\theta \lt\theta_{min}\).(answer check available at lightandmatter.com)
61. A gun is aimed horizontally to the west. The gun is fired, and the bullet leaves the muzzle at \(t=0\). The bullet's position vector as a function of time is \(\mathbf{r}=b\hat{\mathbf{x}}+ct\hat{\mathbf{y}}+dt^2\hat{\mathbf{z}}\), where \(b\), \(c\), and \(d\) are positive constants.
(a) What units would \(b\), \(c\), and \(d\) need to have for the equation to make sense?
(b) Find the bullet's velocity and acceleration as functions of time.
(c) Give physical interpretations of \(b\), \(c\), \(d\), \(\hat{\mathbf{x}}\), \(\hat{\mathbf{y}}\), and \(\hat{\mathbf{z}}\).
62. Annie Oakley, riding north on horseback at 30 mi/hr, shoots her rifle, aiming horizontally and to the northeast. The muzzle speed of the rifle is 140 mi/hr. When the bullet hits a defenseless fuzzy animal, what is its speed of impact? Neglect air resistance, and ignore the vertical motion of the bullet.(solution in the pdf version of the book)
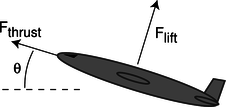
n / Problem 63
63. A cargo plane has taken off from a tiny airstrip in the Andes, and is climbing at constant speed, at an angle of \(\theta=17°\) with respect to horizontal. Its engines supply a thrust of \(F_{thrust}=200\ \text{kN}\), and the lift from its wings is \(F_{lift}=654\ \text{kN}\). Assume that air resistance (drag) is negligible, so the only forces acting are thrust, lift, and weight. What is its mass, in kg? (solution in the pdf version of the book)
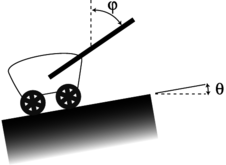
o / Problem 64
64. A wagon is being pulled at constant speed up a slope \(\theta\) by a rope that makes an angle \(\phi\) with the vertical. (a) Assuming negligible friction, show that the tension in the rope is given by the equation
(b) Interpret this equation in the special cases of \(\phi=0\) and \(\phi=180°-\theta\).(solution in the pdf version of the book)
65. The angle of repose is the maximum slope on which an object will not slide. On airless, geologically inert bodies like the moon or an asteroid, the only thing that determines whether dust or rubble will stay on a slope is whether the slope is less steep than the angle of repose.
(a) Find an equation for the angle of repose, deciding for yourself what are the relevant variables.
(b) On an asteroid, where \(g\) can be thousands of times lower than on Earth, would rubble be able to lie at a steeper angle of repose?(solution in the pdf version of the book)
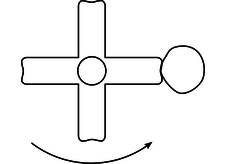
p / Problem 66.
66. When you're done using an electric mixer, you can get most of the batter off of the beaters by lifting them out of the batter with the motor running at a high enough speed. Let's imagine, to make things easier to visualize, that we instead have a piece of tape stuck to one of the beaters.
(a) Explain why static friction has no effect on whether or not the tape flies off.
(b) Analyze the forces in which the tape participates, using a table the format shown in subsection 3.2.6.
(c) Suppose you find that the tape doesn't fly off when the motor is on a low speed, but at a greater speed, the tape won't stay on. Why would the greater speed change things? [Hint: If you don't invoke any law of physics, you haven't explained it.]
67. Show that the expression \(|\mathbf{v}|^2/r\) has the units of acceleration.
68. A plane is flown in a loop-the-loop of radius 1.00 km. The plane starts out flying upside-down, straight and level, then begins curving up along the circular loop, and is right-side up when it reaches the top. (The plane may slow down somewhat on the way up.) How fast must the plane be going at the top if the pilot is to experience no force from the seat or the seatbelt while at the top of the loop? (answer check available at lightandmatter.com)
69. Find the angle between the following two vectors:
\hwhint{hwhint:anglebetween}(answer check available at lightandmatter.com)
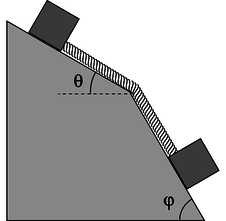
q / Problem 70.
70. The two blocks shown in the figure have equal mass, \(m\), and the surface is frictionless. (a) What is the tension in the massless rope?\hwhint{hwhint:ropeslopes}(answer check available at lightandmatter.com)
(b) Show that the units of your answer make sense.
(c) Check the physical behavior of your answer in the special cases of \(\phi \le \theta\) and \(\theta=0\), \(\phi=90°\).
r / Problem 71.
71. (a) We observe that the amplitude of a certain free oscillation decreases from \(A_\text{o}\) to \(A_\text{o}/Z\) after \(n\) oscillations. Find its \(Q\).(answer check available at lightandmatter.com)
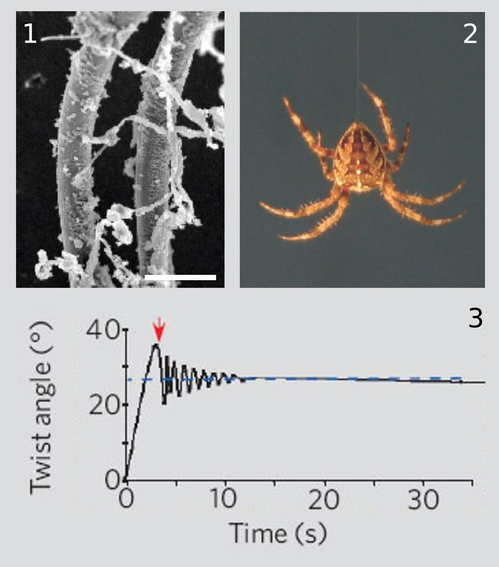
(b) The figure is from Shape memory in Spider draglines, Emile, Le Floch, and Vollrath, Nature 440:621 (2006). Panel 1 shows an electron microscope's image of a thread of spider silk. In 2, a spider is hanging from such a thread. From an evolutionary point of view, it's probably a bad thing for the spider if it twists back and forth while hanging like this. (We're referring to a back-and-forth rotation about the axis of the thread, not a swinging motion like a pendulum.) The authors speculate that such a vibration could make the spider easier for predators to see, and it also seems to me that it would be a bad thing just because the spider wouldn't be able to control its orientation and do what it was trying to do. Panel 3 shows a graph of such an oscillation, which the authors measured using a video camera and a computer, with a 0.1 g mass hung from it in place of a spider. Compared to human-made fibers such as kevlar or copper wire, the spider thread has an unusual set of properties:
- It has a low \(Q\), so the vibrations damp out quickly.
- It doesn't become brittle with repeated twisting as a copper wire would.
- When twisted, it tends to settle in to a new equilibrium angle, rather than insisting on returning to its original angle. You can see this in panel 2, because although the experimenters initially twisted the wire by 35 degrees, the thread only performed oscillations with an amplitude much smaller than \(\pm35\) degrees, settling down to a new equilibrium at 27 degrees.
- Over much longer time scales (hours), the thread eventually resets itself to its original equilbrium angle (shown as zero degrees on the graph). (The graph reproduced here only shows the motion over a much shorter time scale.) Some human-made materials have this “memory” property as well, but they typically need to be heated in order to make them go back to their original shapes.
Focusing on property number 1, estimate the \(Q\) of spider silk from the graph.(answer check available at lightandmatter.com)
72. A cross-country skier is gliding on a level trail, with negligible friction. Then, when he is at position \(x=0\), the tip of his skis enters a patch of dirt. As he rides onto the dirt, more and more of his weight is being supported by the dirt. The skis have length \(\ell\), so if he reached \(x=\ell\) without stopping, his weight would be completely on the dirt. This problem deals with the motion for \(x\lt\ell\). (a) Find the acceleration in terms of \(x\), as well as any other relevant constants.
(b) This is a second-order differential equation. You should be able to find the solution simply by thinking about some commonly occuring functions that you know about, and finding two that have the right properties. If these functions are \(x=f(t)\) and \(x=g(t)\), then the most general solution to the equations of motion will be of the form \(x=af+bg\), where \(a\) and \(b\) are constants to be determined from the initial conditions.
(c) Suppose that the initial velocity \(v_\text{o}\) at \(x=0\) is such that he stops at \(x\lt\ell\). Find the time until he stops, and show that, counterintuitively, this time is independent of \(v_\text{o}\). Explain physically why this is true.(answer check available at lightandmatter.com)
73. A microwave oven works by twisting molecules one way and then the other, counterclockwise and then clockwise about their own centers, millions of times a second. If you put an ice cube or a stick of butter in a microwave, you'll observe that the solid doesn't heat very quickly, although eventually melting begins in one small spot. Once this spot forms, it grows rapidly, while the rest of the solid remains solid; it appears that a microwave oven heats a liquid much more rapidly than a solid. Explain why this should happen, based on the atomic-level description of heat, solids, and liquids. (See, e.g., figure b on page 110.)
Don't repeat the following common mistakes:
In a solid, the atoms are packed more tightly and have less space between them. Not true. Ice floats because it's less dense than water.
In a liquid, the atoms are moving much faster. No, the difference in average speed between ice at \(-1°\text{C}\) and water at \(1°\text{C}\) is only 0.4%.
74. Problem 2-16 on page 120 was intended to be solved using conservation of energy. Solve the same problem using Newton's laws.
75. A bead slides down along a piece of wire that is in the shape of a helix. The helix lies on the surface of a vertical cylinder of radius \(r\), and the vertical distance between turns is \(d\).
(a) Ordinarily when an object slides downhill under the influence of kinetic friction, the velocity-independence of kinetic friction implies that the acceleration is constant, and therefore there is no limit to the object's velocity. Explain the physical reason why this argument fails here, so that the bead will in fact have some limiting velocity.
(b) Find the limiting velocity.
(c) Show that your result has the correct behavior in the limit of \(r \rightarrow \infty\). [Problem by B. Korsunsky.](answer check available at lightandmatter.com)
76. A person on a bicycle is to coast down a ramp of height \(h\) and then pass through a circular loop of radius \(r\). What is the smallest value of \(h\) for which the cyclist will complete the loop without falling? (Ignore the kinetic energy of the spinning wheels.)(answer check available at lightandmatter.com)
77. A car accelerates from rest. At low speeds, its acceleration is limited by static friction, so that if we press too hard on the gas, we will “burn rubber” (or, for many newer cars, a computerized traction-control system will override the gas pedal). At higher speeds, the limit on acceleration comes from the power of the engine, which puts a limit on how fast kinetic energy can be developed.
(a) Show that if a force \(F\) is applied to an object moving at speed \(v\), the power required is given by \(P=vF\).
(b) Find the speed \(v\) at which we cross over from the first regime described above to the second. At speeds higher than this, the engine does not have enough power to burn rubber. Express your result in terms of the car's power \(P\), its mass \(m\), the coefficient of static friction \(\mu_s\), and \(g\).(answer check available at lightandmatter.com)
(c) Show that your answer to part b has units that make sense.
(d) Show that the dependence of your answer on each of the four variables makes sense physically.
(e) The 2010 Maserati Gran Turismo Convertible has a maximum power of \(3.23\times10^5\ \text{W}\) (433 horsepower) and a mass (including a 50-kg driver) of \(2.03\times10^3\ \text{kg}\). (This power is the maximum the engine can supply at its optimum frequency of 7600 r.p.m. Presumably the automatic transmission is designed so a gear is available in which the engine will be running at very nearly this frequency when the car is at moving at \(v\).) Rubber on asphalt has \(\mu_s\approx0.9\). Find \(v\) for this car. Answer: \(18\ \text{m}/\text{s}\), or about 40 miles per hour.
(f) Our analysis has neglected air friction, which can probably be approximated as a force proportional to \(v^2\). The existence of this force is the reason that the car has a maximum speed, which is 176 miles per hour. To get a feeling for how good an approximation it is to ignore air friction, find what fraction of the engine's maximum power is being used to overcome air resistance when the car is moving at the speed \(v\) found in part e. Answer: 1%
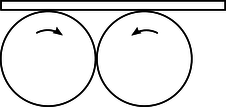
s / Problem 78.
78. Two wheels of radius \(r\) rotate in the same vertical plane with angular velocities \(+\Omega\) and \(-\Omega\) about axes that are parallel and at the same height. The wheels touch one another at a point on their circumferences, so that their rotations mesh like gears in a gear train. A board is laid on top of the wheels, so that two friction forces act upon it, one from each wheel. Characterize the three qualitatively different types of motion that the board can exhibit, depending on the initial conditions.
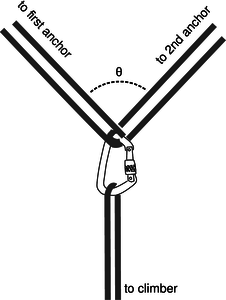
t / Problem 79.
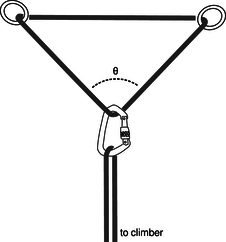
79. For safety, mountain climbers often wear a climbing harness and tie in to other climbers on a rope team or to anchors such as pitons or snow anchors. When using anchors, the climber usually wants to tie in to more than one, both for extra strength and for redundancy in case one fails. The figure shows such an arrangement, with the climber hanging from a pair of anchors forming a “Y” at an angle \(\theta\). The usual advice is to make \(\theta\lt90°\); for large values of \(\theta\), the stress placed on the anchors can be many times greater than the actual load \(L\), so that two anchors are actually less safe than one.
(a) Find the force \(S\) at each anchor in terms of \(L\) and \(\theta\). (answer check available at lightandmatter.com)
(b) Verify that your answer makes sense in the case of \(\theta=0\).
(c) Interpret your answer in the case of \(\theta=180°\).
(d) What is the smallest value of \(\theta\) for which \(S\) equals or exceeds \(L\), so that for larger angles a failure of at least one anchor is more likely than it would have been with a single anchor?(answer check available at lightandmatter.com)
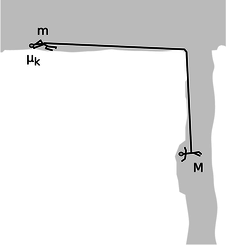
u / Problem 80.
80. Mountain climbers with masses \(m\) and \(M\) are roped together while crossing a horizontal glacier when a vertical crevasse opens up under the climber with mass \(M\). The climber with mass \(m\) drops down on the snow and tries to stop by digging into the snow with the pick of an ice ax. Alas, this story does not have a happy ending, because this doesn't provide enough friction to stop. Both \(m\) and \(M\) continue accelerating, with \(M\) dropping down into the crevasse and \(m\) being dragged across the snow, slowed only by the kinetic friction with coefficient \(\mu_k\) acting between the ax and the snow. There is no significant friction between the rope and the lip of the crevasse.
(a) Find the acceleration \(a\).(answer check available at lightandmatter.com)
(b) Check the units of your result.
(c) Check the dependence of your equation on the variables. That means that for each variable, you should determine what its effect on \(a\) should be physically, and then what your answer from part a says its effect would be mathematically.
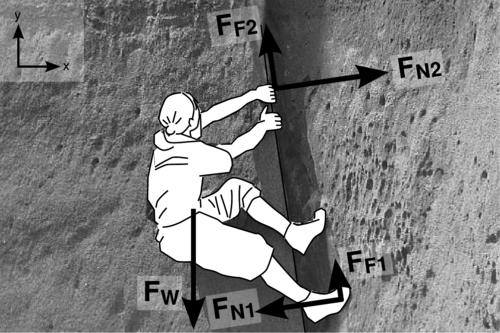
v / Problem 81.
81. Complete example 71 on p. 205 by expressing the remaining nine \(x\) and \(y\) components of the forces in terms of the five magnitudes and the small, positive angle \(\theta\approx9°\) by which the crack overhangs. (answer check available at lightandmatter.com)
w / Problem 82.
82. In a well known stunt from circuses and carnivals, a motorcyclist rides around inside a big bowl, gradually speeding up and rising higher. Eventually the cyclist can get up to where the walls of the bowl are vertical. Let's estimate the conditions under which a running human could do the same thing.
(a) If the runner can run at speed \(v\), and her shoes have a coefficient of static friction \(\mu_s\), what is the maximum radius of the circle?(answer check available at lightandmatter.com)
(b) Show that the units of your answer make sense.
(c) Check that its dependence on the variables makes sense.
(d) Evaluate your result numerically for \(v=10\ \text{m}/\text{s}\) (the speed of an olympic sprinter) and \(\mu_s=5\). (This is roughly the highest coefficient of static friction ever achieved for surfaces that are not sticky. The surface has an array of microscopic fibers like a hair brush, and is inspired by the hairs on the feet of a gecko. These assumptions are not necessarily realistic, since the person would have to run at an angle, which would be physically awkward.)(answer check available at lightandmatter.com)
x / Problem 83.
83. Problem 79 discussed a possible correct way of setting up a redundant anchor for mountaineering. The figure for this problem shows an incorrect way of doing it, by arranging the rope in a triangle (which we'll take to be isoceles). One of the bad things about the triangular arrangement is that it requires more force from the anchors, making them more likely to fail. (a) Using the same notation as in problem 79, find \(S\) in terms of \(L\) and \(\theta\). (answer check available at lightandmatter.com)
(b) Verify that your answer makes sense in the case of \(\theta=0\), and compare with the correct setup.
84. At a picnic, someone hands you a can of beer. The ground is uneven, and you don't want to spill your drink. You reason that it will be more stable if you drink some of it first in order to lower its center of mass. How much should you drink in order to make the center of mass as low as possible? [Based on a problem by Walter van B. Roberts and Martin Gardner.]
Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


