4.3: Resonance
- Page ID
- 946
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Resonance is a phenomenon in which an oscillator responds most strongly to a driving force that matches its own natural frequency of vibration. For example, suppose a child is on a playground swing with a natural frequency of 1 Hz. That is, if you pull the child away from equilibrium, release her, and then stop doing anything for a while, she'll oscillate at 1 Hz. If there was no friction, as we assumed in section 2.5, then the sum of her gravitational and kinetic energy would remain constant, and the amplitude would be exactly the same from one oscillation to the next. However, friction is going to convert these forms of energy into heat, so her oscillations would gradually die out. To keep this from happening, you might give her a push once per cycle, i.e., the frequency of your pushes would be 1 Hz, which is the same as the swing's natural frequency. As long as you stay in rhythm, the swing responds quite well. If you start the swing from rest, and then give pushes at 1 Hz, the swing's amplitude rapidly builds up, as in figure a, until after a while it reaches a steady state in which friction removes just as much energy as you put in over the course of one cycle.
self-check:
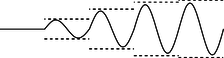
In figure a, compare the amplitude of the cycle immediately following the first push to the amplitude after the second. Compare the energies as well. (answer in the back of the PDF version of the book)
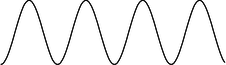
What will happen if you try pushing at 2 Hz? Your first push puts in some momentum, \(p\), but your second push happens after only half a cycle, when the swing is coming right back at you, with momentum \(-p\)! The momentum transfer from the second push is exactly enough to stop the swing. The result is a very weak, and not very sinusoidal, motion, b.

Making the math easy
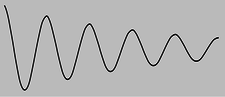
This is a simple and physically transparent example of resonance: the swing responds most strongly if you match its natural rhythm. However, it has some characteristics that are mathematically ugly and possibly unrealistic. The quick, hard pushes are known as impulse forces, c, and they lead to an \(x\)-\(t\) graph that has nondifferentiable kinks.

Impulsive forces like this are not only badly behaved mathematically, they are usually undesirable in practical terms. In a car engine, for example, the engineers work very hard to make the force on the pistons change smoothly, to avoid excessive vibration. Throughout the rest of this section, we'll assume a driving force that is sinusoidal, d, i.e., one whose \(F\)-\(t\) graph is either a sine function or a function that differs from a sine wave in phase, such as a cosine. The force is positive for half of each cycle and negative for the other half, i.e., there is both pushing and pulling. Sinusoidal functions have many nice mathematical characteristics (we can differentiate and integrate them, and the sum of sinusoidal functions that have the same frequency is a sinusoidal function), and they are also used in many practical situations. For instance, my garage door zapper sends out a sinusoidal radio wave, and the receiver is tuned to resonance with it.
A second mathematical issue that I glossed over in the swing example was how friction behaves. In section 3.2.4, about forces between solids, the empirical equation for kinetic friction was independent of velocity. Fluid friction, on the other hand, is velocity-dependent. For a child on a swing, fluid friction is the most important form of friction, and is approximately proportional to \(v^2\). In still other situations, e.g., with a low-density gas or friction between solid surfaces that have been lubricated with a fluid such as oil, we may find that the frictional force has some other dependence on velocity, perhaps being proportional to \(v\), or having some other complicated velocity dependence that can't even be expressed with a simple equation. It would be extremely complicated to have to treat all of these different possibilities in complete generality, so for the rest of this section, we'll assume friction proportional to velocity
\[\begin{equation*} F = -bv , \end{equation*}\]
simply because the resulting equations happen to be the easiest to solve. Even when the friction doesn't behave in exactly this way, many of our results may still be at least qualitatively correct.
3.3.1 Damped, free motion
Numerical treatment
An oscillator that has friction is referred to as damped. Let's use numerical techniques to find the motion of a damped oscillator that is released away from equilibrium, but experiences no driving force after that. We can expect that the motion will consist of oscillations that gradually die out.
In section 2.5, we simulated the undamped case using our tried and true Python function based on conservation of energy. Now, however, that approach becomes a little awkward, because it involves splitting up the path to be traveled into \(n\) tiny segments, but in the presence of damping, each swing is a little shorter than the last one, and we don't know in advance exactly how far the oscillation will get before turning around. An easier technique here is to use force rather than energy. Newton's second law, \(a=F/m\), gives \(a=(-kx-bv)/m\), where we've made use of the result of example 40 for the force exerted by the spring. This becomes a little prettier if we rewrite it in the form
\[\begin{equation*} ma+bv+kx = 0 , \end{equation*}\]
which gives symmetric treatment to three terms involving \(x\) and its first and second derivatives, \(v\) and \(a\). Now instead of calculating the time \(\Delta{}t=\Delta{}x/v\) required to move a predetermined distance \(\Delta{}x\), we pick \(\Delta{}t\) and determine the distance traveled in that time, \(\Delta{}x=v\Delta{}t\). Also, we can no longer update \(v\) based on conservation of energy, since we don't have any easy way to keep track of how much mechanical energy has been changed into heat energy. Instead, we recalculate the velocity using \(\Delta{}v=a\Delta{}t\).
import math
k=39.4784 # chosen to give a period of 1 second
m=1.
b=0.211 # chosen to make the results simple
x=1.
v=0.
t=0.
dt=.01
n=1000
for j in range(n):
x=x+v*dt
a=(-k*x-b*v)/m
if (v>0) and (v+a*dt<0) :
print("turnaround at t=",t,", x=",x)
v=v+a*dt
t=t+dt
turnaround at t= 0.99 , x= 0.899919262445 turnaround at t= 1.99 , x= 0.809844934046 turnaround at t= 2.99 , x= 0.728777519477 turnaround at t= 3.99 , x= 0.655817260033 turnaround at t= 4.99 , x= 0.590154191135 turnaround at t= 5.99 , x= 0.531059189965 turnaround at t= 6.99 , x= 0.477875914756 turnaround at t= 7.99 , x= 0.430013546991 turnaround at t= 8.99 , x= 0.386940256644 turnaround at t= 9.99 , x= 0.348177318484
The spring constant, \(k=4\pi{}=39.4784\) N/m, is designed so that if the undamped equation \(f=(1/2\pi)\sqrt{k/m}\) was still true, the frequency would be 1 Hz. We start by noting that the addition of a small amount of damping doesn't seem to have changed the period at all, or at least not to within the accuracy of the calculation.10 You can check for yourself, however, that a large value of \(b\), say 5 \(\text{N}\!\cdot\!\text{s}/\text{m}\), does change the period significantly.
We release the mass from \(x=1\ \text{m}\), and after one cycle, it only comes back to about \(x=0.9\ \text{m}\). I chose \(b=0.211\ \text{N}\!\cdot\!\text{s}/\text{m}\) by fiddling around until I got this result, since a decrease of exactly 10% is easy to discuss. Notice how the amplitude after two cycles is about \(0.81\ \text{m}\), i.e., \(1\ \text{m}\) times \(0.9^2\): the amplitude has again dropped by exactly 10%. This pattern continues for as long as the simulation runs, e.g., for the last two cycles, we have 0.34818/0.38694=0.89982, or almost exactly 0.9 again. It might have seemed capricious when I chose to use the unrealistic equation \(F=-bv\), but this is the payoff. Only with \(-bv\) friction do we get this kind of mathematically simple exponential decay.
Because the decay is exponential, it never dies out completely; this is different from the behavior we would have had with Coulomb friction, which does make objects grind completely to a stop at some point. With friction that acts like \(F=-bv\), \(v\) gets smaller as the oscillations get smaller. The smaller and smaller force then causes them to die out at a rate that is slower and slower.
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


