2.4: Newton's Second Law of Motion- Force and Acceleration
- Page ID
- 46154
Learning Objectives
- Define net force, external force, and system.
- Understand Newton’s second law of motion.
- Apply Newton’s second law to determine the weight of an object.
Newton’s second law of motion is closely related to Newton’s first law of motion. It mathematically states the cause and effect relationship between force and changes in motion. Newton’s second law of motion is more quantitative and is used extensively to calculate what happens in situations involving a force. Before we can write down Newton’s second law as a simple equation giving the exact relationship of force, mass, and acceleration, we need to sharpen some ideas that have already been mentioned.
First, what do we mean by a change in motion? The answer is that a change in motion is equivalent to a change in velocity. A change in velocity means, by definition, that there is an acceleration. Newton’s first law says that a net external force causes a change in motion; thus, we see that a net external force causes acceleration.
Another question immediately arises. What do we mean by an external force? An intuitive notion of external is correct—an external force acts from outside the system of interest. For example, in Figure \(\PageIndex{1}\)(a) the system of interest is the wagon plus the child in it. The two forces exerted by the other children are external forces. An internal force acts between elements of the system. Again looking at Figure \(\PageIndex{1}\)(a), the force the child in the wagon exerts to hang onto the wagon is an internal force between elements of the system of interest. Only external forces affect the motion of a system, according to Newton’s first law. (The internal forces actually cancel, as we shall see in the next section.) You must define the boundaries of the system before you can determine which forces are external. Sometimes the system is obvious, whereas other times identifying the boundaries of a system is more subtle. The concept of a system is fundamental to many areas of physics, as is the correct application of Newton’s laws. This concept will be revisited many times on our journey through physics.
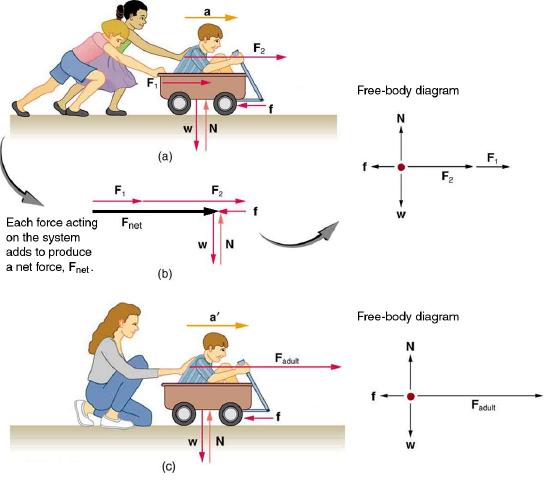
Figure \(\PageIndex{1}\) is our first example of a free-body diagram, which is a technique used to illustrate all the external forces acting on a body. The body is represented by a single isolated point (or free body), and only those forces acting on the body from the outside (external forces) are shown. Free-body diagrams are very useful in analyzing forces acting on a system and are employed extensively in the study and application of Newton’s laws of motion.
Now, it seems reasonable that acceleration should be directly proportional to and in the same direction as the net (total) external force acting on a system. This assumption has been verified experimentally and is illustrated in Figure \(\PageIndex{1}\). In part (a), a smaller force causes a smaller acceleration than the larger force illustrated in part (c). For completeness, the vertical forces are also shown; they are assumed to cancel since there is no acceleration in the vertical direction. The vertical forces are the weight \(w\) and the support of the ground \(N\), and the horizontal force \(f\) represents the force of friction. These will be discussed in more detail in later sections. For now, we will say that friction is a force that opposes the motion past each other of objects that are touching. Figure \(\PageIndex{1}\)(b) shows how vectors representing the external forces add together to produce a net force, \(\boldsymbol{F}_{\text {net }}\).
To obtain an equation for Newton’s second law, we first write the relationship of acceleration and net external force as the proportionality
\[\boldsymbol{a} \propto \boldsymbol{F}_{\text {net }} \nonumber \]
where the symbol ∝ means “proportional to,” and \(\boldsymbol{F}_{\text {net }}\) is the net external force, the vector sum of all external forces. This proportionality states what we have said in words—acceleration is directly proportional to the net external force. Once the system of interest is chosen, it is important to identify the external forces, so that the internal forces can be ignored (again, as we will see later, they exactly cancel out, allowing for a tremendous simplification).
Now, hopefully it also seems reasonable that acceleration should be inversely proportional to the mass of the system. That is, if the system has more “stuff”, then for the same net external force applied, the acceleration is less. And indeed, as illustrated in Figure \(\PageIndex{2}\), the same net external force applied to a car produces a much smaller acceleration than when applied to a basketball. The proportionality is written as
\[a \propto \frac{1}{m} \nonumber \]
where \(m\) is the mass of the system. In fact, this is how we will define mass. That is, for an object B to have double the mass of an object A, the same net external force applied on object B produces half the acceleration it does on object A.
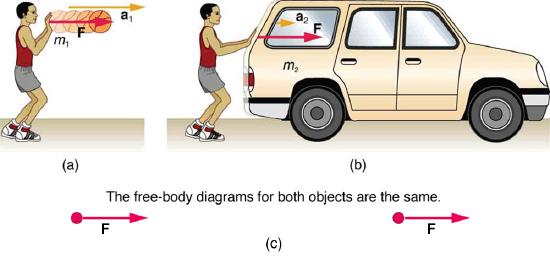
As it turns out, the acceleration of an object depends only on the net external force and the mass of the object. Combining the two proportionalities just given yields Newton's second law of motion.
NEWTON’S SECOND LAW OF MOTION
The acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system, and inversely proportional to its mass.
In equation form, Newton’s second law of motion is
\[\boldsymbol{a}=\frac{\boldsymbol{F}_{\text {net }}}{m} \nonumber \]
This is often written in the more familiar form
\[\boldsymbol{F}_{\text {net }}=m \boldsymbol{a}, \nonumber \]
with the vector notation indicating that the net external force is in the same direction as acceleration. When only the magnitude of force and acceleration are considered, this equation is simply (note the lack of vector notations)
\[F_{\text {net }}=m a . \nonumber \]
Although these equations are really the same, the first gives more insight into what Newton’s second law means. The law is a cause and effect relationship among three quantities. That is, acceleration is caused by a net external force, not vice versa, as the second equation might mistakenly imply.
Units of Force
\(F_{\text {net }}=m a\) is used to define the units of force in terms of the three basic units for mass, length, and time. The SI unit of force is called the newton (abbreviated N) and 1 N is the force needed to accelerate a system of mass 1 kg at the rate of \(1 \mathrm{~m} / \mathrm{s}^{2}\). Putting these together,
\[1 \mathrm{~N}=1 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2}. \nonumber \]
While almost the entire world uses the newton for the unit of force, in the United States the most familiar unit of force is the pound (lb), where 1 N = 0.225 lb.
Weight and the Gravitational Force
When an object is dropped, it accelerates toward the center of Earth. Newton’s second law states that a net force on an object is responsible for its acceleration. If air resistance is negligible, the net force on a falling object is the gravitational force, commonly called its weight, \(w\). Weight can be denoted as a vector \(w\) because it has a direction; down is, by definition, the direction of gravity, so \(w\) is directed downward. The magnitude of weight is denoted as \(w\). Galileo was instrumental in showing that, in the absence of air resistance, all objects fall with the same acceleration \(g\). Using Galileo’s result and Newton’s second law, we can derive an equation for the magnitude of weight.
Consider an object with mass \(m\) falling downward toward Earth. It experiences only the downward force of gravity, which has magnitude \(w\). Newton’s second law states that the magnitude of the net external force on an object is \(F_{\text {net }}=m a \).
Since the object experiences only the downward force of gravity, \(F_{\text {net }}=w\). We know that the acceleration of an object due to gravity is \(g\), or \(a=g\). Substituting these into Newton’s second law gives
Definition: WEIGHT
This is the equation for weight—the gravitational force on a mass \(m\):
\[w=m g. \nonumber \]
Since \(g=9.80 \mathrm{~m} / \mathrm{s}^{2}\) on Earth, the weight of a 1.0 kg object on Earth is 9.8 N, as we see:
\[w=m g=(1.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)=9.8 \mathrm{~N}. \nonumber \]
When the net external force on an object is its weight, we say that it is in free-fall. That is, the only force acting on the object is the force of gravity. In the real world, when objects fall downward toward Earth, they are never truly in free-fall because there is always some upward force from the air acting on the object.
The acceleration due to gravity \(g\) varies slightly over the surface of Earth, so that the weight of an object depends on location and is not an intrinsic property of the object. Weight varies dramatically if one leaves Earth. On the Moon, for example, the acceleration due to gravity is only \(1.67 \mathrm{~m} / \mathrm{s}^{2}\). A 1.0-kg mass thus has a weight of 9.8 N on Earth and only about 1.7 N on the Moon.
The broadest definition of weight in this sense is that the weight of an object is the gravitational force on it from the nearest large body, such as Earth, the Moon, the Sun, and so on. This is the most common and useful definition of weight in physics. It differs dramatically, however, from the definition of weight used by NASA and the popular media in relation to space travel and exploration. When they speak of “weightlessness” and “microgravity,” they are really referring to the phenomenon we call “free-fall” in physics. We shall use the above definition of weight, and we will make careful distinctions between free-fall and actual weightlessness.
It is important to be aware that weight and mass are very different physical quantities, although they are closely related. Mass is the quantity of matter (how much “stuff”) and does not vary, whereas weight is the gravitational force and does vary depending on gravity. It is tempting to equate the two, since most of our examples take place on Earth, where the weight of an object only varies a little with the location of the object. Furthermore, the terms mass and weight are used interchangeably in everyday language; for example, our medical records often show our “weight” in kilograms, but never in the correct units of newtons.
COMMON MISCONCEPTIONS: MASS VS. WEIGHT
Mass and weight are often used interchangeably in everyday language. However, in science, these terms are distinctly different from one another. Mass is a measure of how much matter is in an object. The typical measure of mass is the kilogram (or the “slug” in English units). Weight, on the other hand, is a measure of the force of gravity acting on an object. Weight is equal to the mass of an object (\(m\)) multiplied by the acceleration due to gravity (\(g\)). Like any other force, weight is measured in terms of newtons (or pounds in English units). This interchangeable use is why you might have heard an expression such as, “1 kilogram is 2.2 pounds.” The correct statement is “1 kilogram mass weighs 2.2 pounds on Earth.”
Assuming the mass of an object is kept intact, it will remain the same, regardless of its location. However, because weight depends on the acceleration due to gravity, the weight of an object can change when the object enters into a region with stronger or weaker gravity. For example, the acceleration due to gravity on the Moon is \(1.67 \mathrm{~m} / \mathrm{s}^{2}\) (which is much less than the acceleration due to gravity on Earth, \(9.80 \mathrm{~m} / \mathrm{s}^{2}\)). If you measured your weight on Earth and then measured your weight on the Moon, you would find that you “weigh” much less, even though you do not look any skinnier. This is because the force of gravity is weaker on the Moon. In fact, when people say that they are “losing weight,” they really mean that they are losing “mass” (which in turn causes them to weigh less).
TAKE-HOME EXPERIMENT: MASS AND WEIGHT
What do bathroom scales measure? When you stand on a bathroom scale, what happens to the scale? It depresses slightly. The scale contains springs that compress in proportion to your weight—similar to rubber bands expanding when pulled. The springs provide a measure of your weight (for an object which is not accelerating). This is a force in newtons (or pounds). In most countries, the measurement in newtons is divided by 9.80 to give a reading in mass units of kilograms. The scale measures weight but is calibrated to provide information about mass. While standing on a bathroom scale, push down on a table next to you. What happens to the reading? Why? Would your scale measure the same “mass” on Earth as on the Moon?
Example \(\PageIndex{1}\): What Acceleration Can a Person Produce when Pushing a Lawn Mower?
Suppose that the net external force (push minus friction) exerted on a lawn mower is 51 N (about 11 lb) parallel to the ground. The mass of the mower is 24 kg. What is its acceleration?
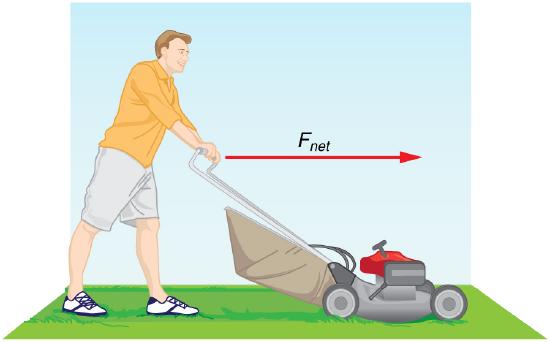
Strategy
Since \(F_{\text {net }}\) and \(m\) are given, the acceleration can be calculated directly from Newton’s second law as stated in \(F_{\text {net }}=ma\).
Solution
The magnitude of the acceleration \(a\) is \(a=\frac{F_{\text {net }}}{m}\). Entering known values gives
\[a=\frac{51 \mathrm{~N}}{24 \mathrm{~kg}} \nonumber\]
Substituting the units \(\mathrm{kg} \cdot \mathrm{m} / \mathrm{s}^{2}\) for N yields
\[a=\frac{51 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^{2}}{24 \mathrm{~kg}}=2.1 \mathrm{~m} / \mathrm{s}^{2}. \nonumber\]
Discussion
The direction of the acceleration is the same direction as that of the net force, which is parallel to the ground. There is no information given in this example about the individual external forces acting on the system, but we can say something about their relative magnitudes. For example, the force exerted by the person pushing the mower forward must be greater than the friction opposing the motion (directed backward) to result in a forward net force, and the vertical forces must cancel if there is to be no acceleration in the vertical direction. The acceleration found is small enough to be reasonable for a person pushing a mower. When the person reaches the top speed, the acceleration will be zero (no change of velocity) and the force exerted by the person pushing the mower will be equal to the friction opposing the motion.
Example \(\PageIndex{2}\): What Rocket Thrust Accelerates This Sled?
Prior to manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force exerted by each rocket, called its thrust \(T\), for the four-rocket propulsion system shown in Figure \(\PageIndex{4}\). The sled’s initial acceleration is \(49 \mathrm{~m} / \mathrm{s}^{2}\) the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.
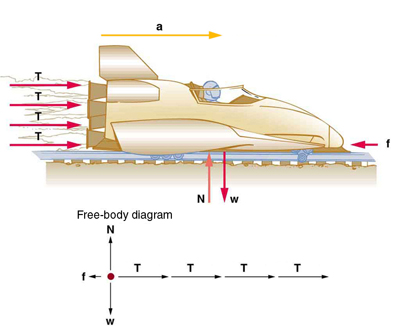
Strategy
Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken as the positive direction. See the free-body diagram in the figure.
Solution
Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of these quantities in the calculations. Hence we begin with
\[F_{\text {net }}=m a, \nonumber\]
where \(F_{\text {net }}\) is the net force along the horizontal direction. We can see from Figure \(\PageIndex{4}\) that the engine thrusts add, while friction opposes the thrust. In equation form, the net external force is
\[F_{\text {net }}=4 T-f. \nonumber\]
Substituting this into Newton’s second law gives
\[F_{\text {net }}=m a=4 T-f. \nonumber\]
Using a little algebra, we solve for the total thrust 4T:
\[4 T=m a+f . \nonumber\]
Substituting known values yields
\[4 T=m a+f=(2100 \mathrm{~kg})\left(49 \mathrm{~m} / \mathrm{s}^{2}\right)+650 \mathrm{~N} . \nonumber\]
So the total thrust is
\[4 T=1.04 \times 10^{5} \mathrm{~N}, \nonumber\]
and the individual thrusts are
\[T=\frac{1.04 \times 10^{5} \mathrm{~N}}{4}=2.6 \times 10^{4} \mathrm{~N}. \nonumber\]
Discussion
The numbers are quite large, so to put the result in perspective, note that acceleration of \(49 \mathrm{~m} / \mathrm{s}^{2}\) is approximately 5 times the gravitational acceleration on Earth. It's a large acceleration, which requires a large net external force to produce.
Experiments such as this were performed in the early 1960s to test the limits of human endurance and the setup designed to protect human subjects in jet fighter emergency ejections. Speeds of 1000 km/h were obtained, with accelerations of 45 \(g^{\prime}\)s. (Recall that \(g\), the acceleration due to gravity, is \(9.80 \mathrm{~m} / \mathrm{s}^{2}\). When we say that an acceleration is \(g^{\prime}\)s, it is \(45 \times 9.80 \mathrm{~m} / \mathrm{s}^{2}\), which is approximately \(440 \mathrm{~m} / \mathrm{s}^{2}\)}.) While living subjects are not used any more, land speeds of 10,000 km/h have been obtained with rocket sleds. In this example, as in the preceding one, the system of interest is obvious. We will see in later examples that choosing the system of interest is crucial—and the choice is not always obvious.
Newton’s second law of motion gives a relationship among acceleration, force, and mass. It can help us make predictions. Each of those physical quantities can be defined independently, so the second law tells us something basic and universal about nature. The next section introduces the third and final law of motion.
Section Summary
- Acceleration, \(a\), is defined as a rate of change in velocity, resulting from a change in the magnitude and/or the direction of the velocity.
- An external force is one acting on a system from outside the system, as opposed to internal forces, which act between components within the system.
- Newton’s second law of motion states that the acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system, and inversely proportional to its mass.
- In equation form, Newton’s second law of motion is \(\boldsymbol{a}=\frac{\boldsymbol{F}_{\text {net }}}{m}\), often written in the more familiar form: \(\boldsymbol{F}_{\text {net }}=m \boldsymbol{a} \).
- The weight \(w\) of an object is defined as the force of gravity acting on an object of mass mm. Given acceleration due to gravity \(g\), the magnitude of weight is:
\[w=m g \nonumber\]
Glossary
- acceleration
- the rate at which an object’s velocity changes over a period of time
- free-fall
- a situation in which the only force acting on an object is the force due to gravity
- external force
- a force acting on an object or system that originates outside of the object or system
- net external force
- the vector sum of all external forces acting on an object or system; causes a mass to accelerate
- free-body diagram
- a sketch showing all of the external forces acting on an object or system; the system is represented by a dot, and the forces are represented by vectors extending outward from the dot
- Newton’s second law of motion
- The acceleration of a system is directly proportional to and in the same direction as the net external force acting on the system, and inversely proportional to its mass.
- system
- the object or the group of objects under consideration
- weight
- the force due to gravity; \(w=mg\) for objects on Earth