2.6: Normal Force and Tension

Learning Objectives

• Define normal force.
• Explain the relationship between normal force and apparent weight.
• Describe properties of tension force.
• Apply Newton's laws of motion to analyze forces.

Forces are given many names, such as push, pull, thrust, lift, weight, friction, and tension. Traditionally, forces have been grouped into several categories and given names relating to their source, how they are transmitted, or their effects. The most important of these categories are discussed in this section, together with some interesting applications. Further examples of forces are discussed later in this text.

Normal Force

Weight (also called force of gravity) is a pervasive force that acts at all times and must be counteracted to keep an object from falling. You definitely notice that you must support the weight of a heavy object by pushing up on it when you hold it stationary, as illustrated in Figure \(\PageIndex{1}\)(a). But how do inanimate objects like a table support the weight of a mass placed on them, such as shown in Figure \(\PageIndex{1}\)(b)? When the bag of dog food is placed on the table, the table actually sags slightly under the load. This would be noticeable if the load were placed on a card table, but even rigid objects deform when a force is applied to them. Unless the object is deformed beyond its limit, it will exert a restoring force much like a deformed spring (or trampoline or diving board). The greater the deformation, the greater the restoring force. So when the load is placed on the table, the table sags until the restoring force becomes as large as the weight of the load. At this point the net external force on the load is zero. That is the situation when the load is stationary on the table. The table sags quickly, and the sag is slight so we do not notice it. But it is similar to the sagging of a trampoline when you climb onto it.

Figure \(\PageIndex{1}\): (a) The person holding the bag of dog food must supply an upward force \(\boldsymbol{F}_{\text {hand }}\) equal in magnitude and opposite in direction to the weight of the food \(w\). (b) The card table sags when the dog food is placed on it, much like a stiff trampoline. Elastic restoring forces in the table grow as it sags until they supply a force N equal in magnitude and opposite in direction to the weight of the load.

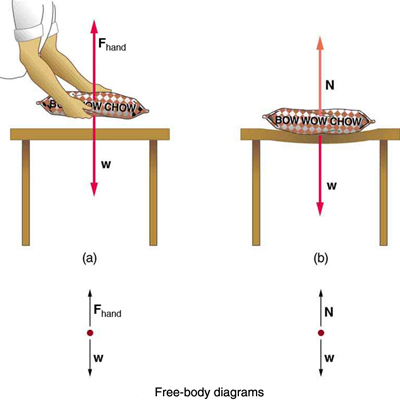
We must conclude that whatever supports a load, be it animate or not, must supply an upward force equal to the weight of the load, as we assumed in a few of the previous examples. The force supporting a load is perpendicular to the surface of contact between the load and its support, and this force is called a normal force, often indicated with symbol N (Please do not confuse this with the abbreviation for newton, the unit of force, N). The word normal means perpendicular to a surface. The normal force is not always equal to the object's weight, if there are other forces acting on the object, or if the object is accelerating, so that the net force is not zero.

Normal force also goes by another name, apparent weight. This is because all the forces you feel, especially your sensation of weight, are directly attributed to contact forces, such as the normal force. When NASA astronauts are weightlessly floating in the International Space Station, their actual weight (gravitational force on them by the Earth) is not zero, but their apparent weight (sensation of weight due to contact forces) is zero.

Tension

A tension is a force along the length of a medium, especially a force carried by a flexible medium, such as a rope or cable. The word “tension” comes from a Latin word meaning “to stretch.” Not coincidentally, the flexible cords that carry muscle forces to other parts of the body are called tendons. Any flexible connector, such as a string, rope, chain, wire, or cable, can exert pulls only parallel to its length; thus, a force carried by a flexible connector is a tension with direction parallel to the connector. It is important to understand that tension is a pull in a connector. In contrast, consider the phrase: “You can’t push a rope.” The tension force pulls outward along the two ends of a rope.

Consider a person holding a mass on a rope as shown in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): When a perfectly flexible connector (one requiring no force to bend it) such as this rope transmits a force T, that force must be parallel to the length of the rope, as shown. The pull such a flexible connector exerts is a tension. Note that the rope pulls with equal force but in opposite directions on the hand and the supported mass (neglecting the weight of the rope). This is an example of Newton’s third law. The rope is the medium that carries the equal and opposite forces between the two objects. The tension anywhere in the rope between the hand and the mass is equal. Once you have determined the tension in one location, you have determined the tension at all locations along the rope.

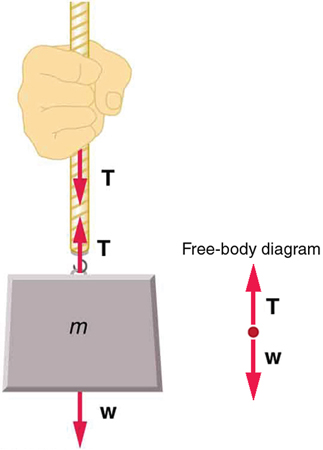
Tension in the rope must equal the weight of the supported mass, as we can prove using Newton’s second law. If the 5.00-kg mass in the figure is stationary, then its acceleration is zero, and thus \(\boldsymbol{F}_{\text {net }}=0\). The only external forces acting on the mass are its weight \(w\) and the tension T supplied by the rope. Thus,

\[F_{\text {net }}=T-w=0, \nonumber \]

where T and \(w\) are the magnitudes of the tension and weight and their signs indicate direction, with up being positive here. Thus, just as you would expect, the tension equals the weight of the supported mass:

\[T=w=m g. \nonumber \]

For a 5.00-kg mass, then (neglecting the mass of the rope) we see that

\[T=m g=(5.00 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)=49.0 \mathrm{~N}. \nonumber\]

If we cut the rope and insert a spring, the spring would extend a length corresponding to a force of 49.0 N, providing a direct observation and measure of the tension force in the rope.

Flexible connectors are often used to transmit forces around corners, such as in a hospital traction system, a finger joint, or a bicycle brake cable. If there is no friction, the tension is transmitted undiminished. Only its direction changes, and it is always parallel to the flexible connector. This is illustrated in Figure \(\PageIndex{3}\) (a) and (b).

Figure \(\PageIndex{3}\): (a) Tendons in the finger carry force  T from the muscles to other parts of the finger, usually changing the force’s direction, but not its magnitude (the tendons are relatively friction free). (b) The brake cable on a bicycle carries the tension T from the handlebars to the brake mechanism. Again, the direction but not the magnitude of T is changed.

Figure \(\PageIndex{4}\): Unless an infinite tension is exerted, any flexible connector—such as the chain at the bottom of the picture—will sag under its own weight, giving a characteristic curve when the weight is evenly distributed along the length, known as a catenary curve. Suspension bridges—such as the Golden Gate Bridge shown in this image—are essentially very heavy flexible connectors. The weight of the bridge is evenly distributed along the length of flexible connectors, usually cables, which take on the characteristic shape. (credit: Leaflet, Wikimedia Commons)

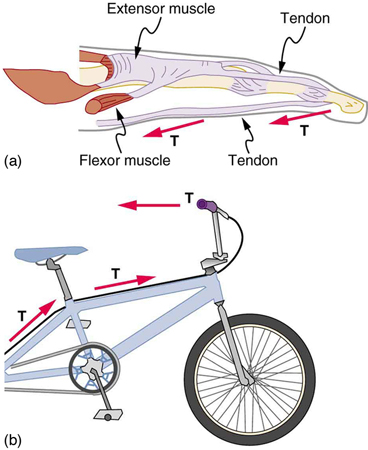
Normal force and tension are examples of forces that are determined not by a specific formula but by enforcing a constraint on motion state of a body. In the example of the bag on a table above, the normal force is equal to weight, because that is the value needed to ensure that the acceleration of the bag is zero. What happens if the body experiences a non-zero acceleration? We will consider example below of a person standing on a scale (which measures his apparent weight) while riding in an elevator.

Example \(\PageIndex{1}\): What Does the Bathroom Scale Read in an Elevator?

Figure \(\PageIndex{5}\) shows a 75.0-kg man (weight of about 165 lb.) standing on a bathroom scale in an elevator. Calculate the scale reading: (a) if the elevator accelerates upward at a rate of \(1.20 \mathrm{~m} / \mathrm{s}^{2}\), and (b) if the elevator moves upward at a constant speed of 1 m/s.

Figure \(\PageIndex{5}\): (a) The various forces acting when a person stands on a bathroom scale in an elevator. The arrows are approximately correct for when the elevator is accelerating upward—broken arrows represent forces too large to be drawn to scale. \(\overrightarrow{\mathbf{T}}\) is the tension in the supporting cable, \(\overrightarrow{\mathbf{w}}\) is the weight of the person, \(\overrightarrow{\mathbf{w}}_{\mathrm{s}}\) is the weight of the scale, \(\overrightarrow{\mathbf{w}}_{\mathrm{e}}\) is the weight of the elevator, \(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\) is the force of the scale on the person, \(\overrightarrow{\mathbf{F}}_{\mathrm{P}}\) is the force of the person on the scale, \(\overrightarrow{\mathbf{F}}_{\mathrm{t}}\) is the force of the scale on the floor of the elevator, and \(\overrightarrow{\mathbf{N}}\) is the force of the floor upward on the scale. (b) The free-body diagram shows only the external forces acting on the designated system of interest—the person—and is the diagram we use for the solution of the problem.

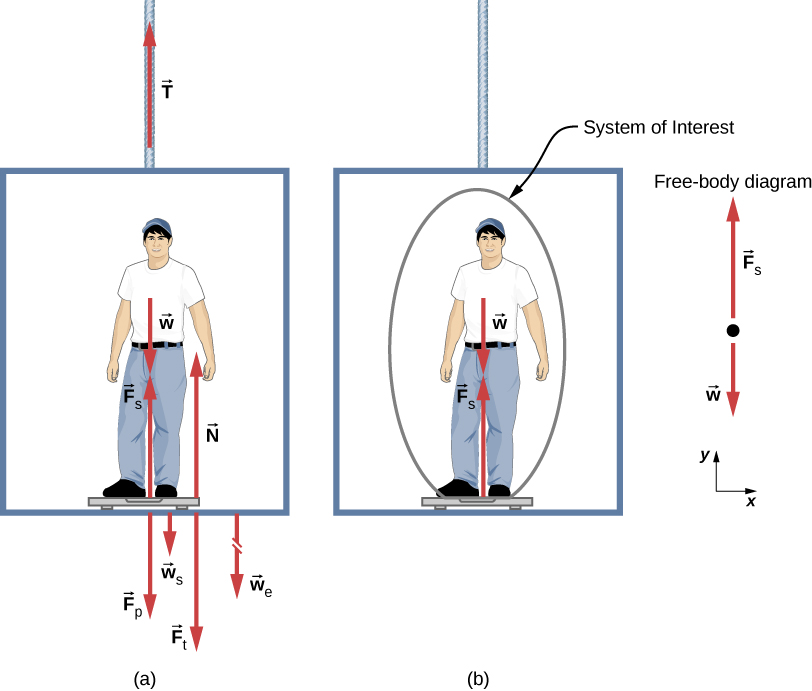
Strategy

If the scale at rest is accurate, its reading equals \(\overrightarrow{\mathbf{F}}_{\mathrm{P}}\), the magnitude of the force the person exerts downward on it. Figure \(\PageIndex{5}\)(a) shows the numerous forces acting on the elevator, scale, and person. It makes this one-dimensional problem look much more formidable than if the person is chosen to be the system of interest and a free-body diagram is drawn, as in Figure \(\PageIndex{5}\)(b). Analysis of the free-body diagram using Newton’s laws can produce answers to both Figure \(\PageIndex{5}\)(a) and (b) of this example, as well as some other questions that might arise. The only forces acting on the person are his weight \(\overrightarrow{\mathbf{w}}\) and the upward force of the scale \(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\). According to Newton’s third law, \(\overrightarrow{\mathbf{F}}_{\mathrm{P}}\) and \(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\) are equal in magnitude and opposite in direction, so that we need to find F_s in order to find what the scale reads. We can do this, as usual, by applying Newton’s second law,

\[\overrightarrow{\mathbf{F}}_{\text {net }}=m \overrightarrow{\mathbf{a}}. \nonumber\]

From the free-body diagram, we see that the net force \(\overrightarrow{\mathbf{F}}_{\text {net }}\) is sum of the scale force \(\overrightarrow{\mathbf{F}}_{\mathrm{s}}\) and the weight \(\overrightarrow{\mathbf{w}}\). Since the scale force and the weight are pointing in opposite directions, in terms of the magnitudes of the vectors,

\[F_{\text {net }}=F_{s}-w=m a. \nonumber\]

Solving for F_s gives us an equation with only one unknown:

\[F_{\mathrm{s}}=m a+w, \nonumber\]

or, because \(w=m g\), simply

\[F_{\mathrm{s}}=m a+m g. \nonumber\]

No assumptions were made about the acceleration, so this solution should be valid for a variety of accelerations in addition to those in this situation. (Note: We are considering the case when the elevator is accelerating upward. If the elevator is accelerating downward, Newton’s second law becomes \(F_{s}-w=-m a \).)

Solution

1. We have \(a=1.20 \mathrm{~m} / \mathrm{s}^{2}\), so that

   \[F_{\mathrm{s}}=(75.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)+(75.0 \mathrm{~kg})\left(1.20 \mathrm{~m} / \mathrm{s}^{2}\right) \nonumber\]

   yielding

   \[F_{\mathrm{s}}=825 \mathrm{~N}. \nonumber\]

2. Now, what happens when the elevator reaches a constant upward velocity? Will the scale still read more than his weight? For any constant velocity—up, down, or stationary—acceleration is zero because \(a=\frac{\Delta v}{\Delta t}\) and \(\Delta v=0\). Thus,

   \[F_{\mathrm{s}}=m a+m g=0+m g \nonumber\]

   or

   \[F_{\mathrm{s}}=(75.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right), \nonumber\]

   
   which gives

   \[F_{\mathrm{s}}=735 \mathrm{~N}. \nonumber\]

Significance

The scale reading in Figure \(\PageIndex{5}\)(a) is about 185 lb. What would the scale have read if he were stationary? Since his acceleration would be zero, the force of the scale would be equal to his weight:

\[\begin{gathered}
F_{\text {net }}=m a=0=F_{\mathrm{s}}-w \\
F_{\mathrm{s}}=w=m g \\
F_{\mathrm{s}}=(75.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)=735 \mathrm{~N}.
\end{gathered} \nonumber\]

Thus, the scale reading in the elevator is greater than his 735-N (165-lb.) weight. This means that the scale is pushing up on the person with a force greater than his weight, as it must in order to accelerate him upward. Clearly, the greater the acceleration of the elevator, the greater the scale reading, consistent with what you feel in rapidly accelerating versus slowly accelerating elevators. In Figure \(\PageIndex{5}\)(b), the scale reading is 735 N, which equals the person’s weight. This is the case whenever the elevator has a constant velocity—moving up, moving down, or stationary.

Section Summary

• When objects rest on a surface, the surface applies a force to the object that supports the weight of the object. This supporting force acts perpendicular to and away from the surface. It is called a normal force, and it also goes by the name "apparent weight."
• When objects rest on a non-accelerating horizontal surface, the magnitude of the normal force is equal to the weight of the object:

  \[N=m g. \nonumber\]

• The pulling force that acts along a stretched flexible connector, such as a rope or cable, is called tension, T. When a rope supports the weight of an object that is at rest, the tension in the rope is equal to the weight of the object:

  \[T=m g. \nonumber\]

Glossary

normal force

the force that a surface applies to an object to support the weight of the object; acts perpendicular to the surface on which the object rests

apparent weight

sensation of weight due to contact forces; usually the same as normal force

tension

the pulling force that acts along a medium, especially a stretched flexible connector, such as a rope or cable; when a rope supports the weight of an object, the force on the object due to the rope is called a tension force