2.10: Centripetal Force

Learning Objectives

• Explain the role of centripetal force in a uniform circular motion.
• Calculate centripetal force and acceleration for simple situations.

Any force or combination of forces can cause a centripetal or radial acceleration. Just a few examples are the tension in the rope on a tether ball, the force of Earth’s gravity on the Moon, friction between roller skates and a rink floor, a banked roadway’s force on a car, and forces on the tube of a spinning centrifuge.

Any net force causing uniform circular motion is called a centripetal force. The direction of a centripetal force is toward the center of curvature, the same as the direction of centripetal acceleration. According to Newton’s second law of motion, net force is mass times acceleration: \(F_{\text {net }}=m a\). For uniform circular motion, the acceleration is the centripetal acceleration— \(a=a_{c}\). Thus, the magnitude of centripetal force \(F_{c}\) is

\[F_{\mathrm{c}}=m a_{\mathrm{c}}. \nonumber \]

By using the expressions for centripetal acceleration \(a_{c}\) from \(a_{c}=\frac{v^{2}}{r}\), we get an expression for the centripetal force \(\mathrm{F}_{\mathrm{c}}\) in terms of mass, velocity, and radius of curvature:

\[F_{c}=m \frac{v^{2}}{r}. \nonumber \]

Note that if you solve the first expression for \(r\), you get

\[r=\frac{m v^{2}}{F_{c}}. \nonumber \]

This implies that for a given mass and velocity, a large centripetal force causes a small radius of curvature—that is, a tight curve.

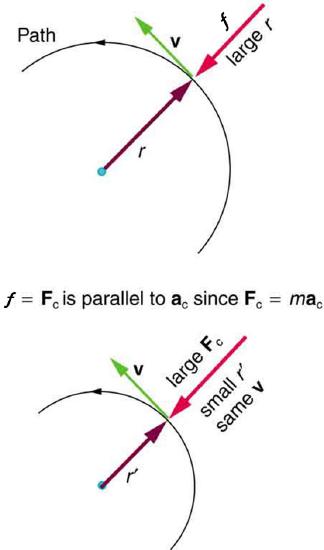
Figure \(\PageIndex{1}\): The frictional force supplies the centripetal force and is numerically equal to it. Centripetal force is perpendicular to velocity and causes uniform circular motion. The larger the \(F_{c}\), the smaller the radius of curvature \(r\) and the sharper the curve. The second curve has the same \(v\), but a larger \(F_{c}\) produces a smaller \(r^{\prime}\).

Example \(\PageIndex{1}\): What Coefficient of Friction Do Car Tires Need on a Flat Curve?

(a) Calculate the centripetal force exerted on a 900 kg car that negotiates a 500 m radius curve at 25.0 m/s.

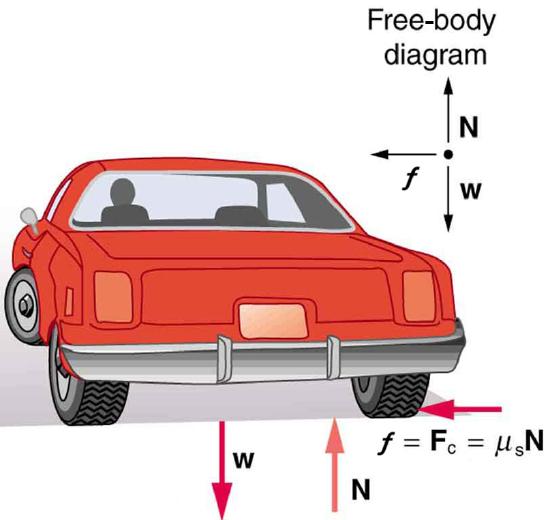
(b) Assuming an unbanked curve, find the minimum static coefficient of friction, between the tires and the road, static friction being the reason that keeps the car from slipping (see Figure \(\PageIndex{2}\)).

Strategy and Solution for (a)

We know that \(F_{\mathrm{c}}=\frac{m v^{2}}{r}\). Thus,

\[F_{\mathrm{c}}=\frac{m v^{2}}{r}=\frac{(900 \mathrm{~kg})(25.0 \mathrm{~m} / \mathrm{s})^{2}}{(500 \mathrm{~m})}=1125 \mathrm{~N}. \nonumber\]

Strategy for (b)

Figure \(\PageIndex{2}\) shows the forces acting on the car on an unbanked (level ground) curve. Friction is to the left, keeping the car from slipping, and because it is the only horizontal force acting on the car, the friction is the centripetal force in this case. We know that the maximum static friction (at which the tires roll but do not slip) is \(\mu_{\mathrm{s}} N\), where \(\mu_{\mathrm{s}}\) is the static coefficient of friction and \(N\) is the normal force. The normal force equals the car’s weight on level ground, so that \(N=m g \). Thus the centripetal force in this situation is

\[F_{\mathrm{c}}=f=\mu_{\mathrm{s}} N=\mu_{\mathrm{s}} m g. \nonumber\]

Now we have a relationship between centripetal force and the coefficient of friction. Using the expression for \(\mathrm{F}_{\mathrm{c}}\)

\[\begin{gathered}
F_{c}=m \frac{v^{2}}{r}, \\
m \frac{v^{2}}{r}=\mu_{\mathrm{s}} m g .
\end{gathered} \nonumber\]

We solve this for \(\mu_{\mathrm{s}}\), noting that mass cancels, and obtain

\[\mu_{\mathrm{s}}=\frac{v^{2}}{r g}. \nonumber\]

Solution for (b)

Substituting the knowns,

\[\mu_{\mathrm{s}}=\frac{(25.0 \mathrm{~m} / \mathrm{s})^{2}}{(500 \mathrm{~m})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)}=0.13. \nonumber\]

(Because coefficients of friction are approximate, the answer is given to only two digits.)

Discussion

The coefficient of friction found in part (b) is much smaller than is typically found between tires and roads. The car will still negotiate the curve if the coefficient is greater than 0.13, because static friction is a responsive force, being able to assume a value less than but no more than \(\mu_{\mathrm{s}} N\). A higher coefficient would also allow the car to negotiate the curve at a higher speed, but if the coefficient of friction is less, the safe speed would be less than 25 m/s. Note that mass cancels, implying that in this example, it does not matter how heavily loaded the car is to negotiate the turn. Mass cancels because friction is assumed proportional to the normal force, which in turn is proportional to mass. If the surface of the road were banked, the normal force would be less as will be discussed below.

Figure \(\PageIndex{2}\): This car on level ground is moving away and turning to the left. The centripetal force causing the car to turn in a circular path is due to friction between the tires and the road. A minimum coefficient of friction is needed, or the car will move in a larger-radius curve and leave the roadway.

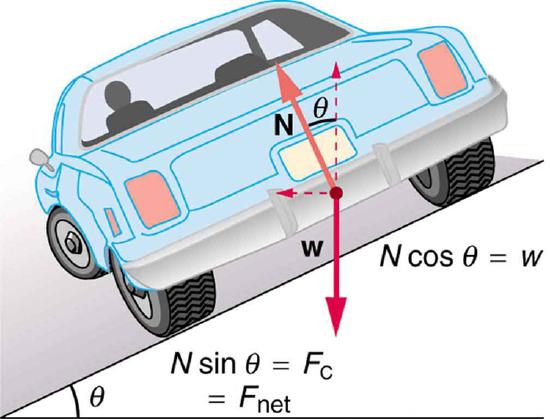
In the case of banked curves, where the slope of the road helps you negotiate the curve, some or all of the necessary centripetal force is provided by the normal force. See Figure \(\PageIndex{3}\). The greater the angle \(\theta\), the faster you can take the curve. Race tracks for bikes as well as cars, for example, often have steeply banked curves. In an “ideally banked curve,” the angle \(\theta\) is such that you can negotiate the curve at a certain speed without the aid of friction between the tires and the road. Conceptually, for ideal banking, the net external force equals the horizontal centripetal force in the absence of friction. The components of the normal force N in the horizontal and vertical directions must equal the centripetal force and the weight of the car, respectively.

Figure \(\PageIndex{3}\) shows a free body diagram for a car on a frictionless banked curve. If the angle \(\theta\) is ideal for the speed and radius, then the net external force will equal the necessary centripetal force. The only two external forces acting on the car are its weight \(w\) and the normal force of the road \(N\). (A frictionless surface can only exert a force perpendicular to the surface—that is, a normal force.) These two forces must add to give a net external force that is horizontal toward the center of curvature and has magnitude \(\mathrm{mv}^{2} / \mathrm{r}\). We omit detailed calculations, which require trigonometry.

Figure \(\PageIndex{3}\): The car on this banked curve is moving away and turning to the left.

Section Summary

• Centripetal force \(\mathrm{F}_{\mathrm{c}}\) is any force causing uniform circular motion. It is a “center-seeking” force that always points toward the center of rotation. It is perpendicular to linear velocity \(v\) and has magnitude

  \[F_{\mathrm{c}}=m a_{\mathrm{c}}, \nonumber\]

  which can also be expressed as

  \[F_{c}=m \frac{v^{2}}{r}. \nonumber\]

Glossary

centripetal force

any net force causing uniform circular motion

ideal banking

the sloping of a curve in a road, where the angle of the slope allows the vehicle to negotiate the curve at a certain speed without the aid of friction between the tires and the road; the net external force on the vehicle equals the horizontal centripetal force in the absence of friction

banked curve

the curve in a road that is sloping in a manner that helps a vehicle negotiate the curve