3.5: Conservative Forces, Potential Energy, and Conservation of Energy
- Page ID
- 46166
Learning Objectives
- Define conservative force, potential energy, and mechanical energy.
- Apply conservation of mechanical energy to simple physical situations.
- Explain the law of the conservation of energy.
- Describe some of the many forms of energy.
Potential Energy and Conservative Forces
Work is done by a force, and some forces, such as weight, have special characteristics. A conservative force is one, like the gravitational force, for which work done by or against it depends only on the starting and ending points of a motion and not on the path taken. This happens if the force is a function of position alone and not time, velocity, or other parameters. We can define a potential energy (PE) for any conservative force, just as we did for the gravitational force. For example, when you wind up a toy, an egg timer, or an old-fashioned watch, you do work against its spring and store energy in it. (We treat these springs as ideal, in that we assume there is no friction and no production of thermal energy.) This stored energy is recoverable as work, and it is useful to think of it as potential energy contained in the spring. Indeed, the reason that the spring has this characteristic is that its force is conservative. That is, a conservative force results in stored or potential energy. Gravitational potential energy is one example, as is the energy stored in a spring. We will also see how conservative forces are related to the conservation of energy.
POTENTIAL ENERGY AND CONSERVATIVE FORCES
Potential energy is the energy a system has due to position, shape, or configuration. It is stored energy that is completely recoverable.
A conservative force is a force that is a function of position alone, with the result that the work done by the force depends only on the starting and ending points of a motion and not on the particular path taken.
Change in potential energy comes from the work done against a conservative force. Or flipping this around, potential energy increases as a conservative force does a negative work. That is,
\[\Delta \mathrm{PE}=-W_{c}, \nonumber \]
where \(W_{c}\) is work done by a conservative force.
Conservation of Mechanical Energy
Consider an object in a system. If it gains any kinetic energy, this is a result of a net work done on the object, according to the work-kinetic energy theorem. If only conservative forces, such as the gravitational force or a spring force, do work in this system, then as kinetic energy increases with the net work done by the conservative forces, the system loses potential energy. That is, \(\Delta \mathrm{KE}=W_{c}=-\Delta \mathrm{PE}\). In other words,
\[\Delta \mathrm{KE}+\Delta \mathrm{PE}=0. \nonumber \]
This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces. That is,
\[
\left.\begin{array}{l}
\text { or } \begin{array}{l}
\mathrm{KE}+\mathrm{PE}=\text { constant } \\ \\[4pt]
\mathrm{KE}_{\mathrm{i}}+\mathrm{PE}_{\mathrm{i}}=\mathrm{KE}_{\mathrm{f}}+\mathrm{PE}_{\mathrm{f}}
\end{array}
\end{array}\right\} \text { (conservative forces only), } \nonumber \]
where i and f denote initial and final values. This equation is a form of the work-energy theorem for conservative forces; it is known as the conservation of mechanical energy principle. Remember that this applies to the extent that all the forces are conservative, so that friction is negligible. The total kinetic plus potential energy of a system is defined to be its mechanical energy, (KE+PE). In a system that experiences only conservative forces, there is a potential energy associated with each force, and the energy only changes form between KE and the various types of PE, with the total energy remaining constant.
Example \(\PageIndex{1}\): Using Conservation of Mechanical Energy to Calculate the Speed of a Toy Car
A 0.100-kg toy car is propelled by a compressed spring, as shown in Figure \(\PageIndex{1}\). The car follows a track that rises 0.180 m above the starting point. The compressed spring has a potential energy of 0.200 J. Assuming work done by friction to be negligible, find (a) how fast the car is going before it starts up the slope and (b) how fast it is going at the top of the slope.
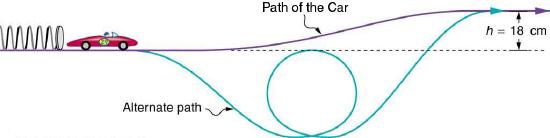
Strategy
The spring force and the gravitational force are conservative forces, so conservation of mechanical energy can be used. Thus,
\[\mathrm{KE}_{\mathrm{i}}+\mathrm{PE}_{\mathrm{i}}=\mathrm{KE}_{\mathrm{f}}+\mathrm{PE}_{\mathrm{f}} \nonumber\]
or
\[\frac{1}{2} m v_{\mathrm{i}}^{2}+m g h_{\mathrm{i}}+\mathrm{PE}_{\mathrm{si}}=\frac{1}{2} m v_{\mathrm{f}}^{2}+m g h_{\mathrm{f}}+\mathrm{PE}_{\mathrm{sf}} \nonumber\]
where \(h\) is the height (vertical position) and \(\mathrm{PE}_{\mathrm{s}}\) is the potential energy of the spring. This general statement looks complex but becomes much simpler when we start considering specific situations. First, we must identify the initial and final conditions in a problem; then, we enter them into the last equation to solve for an unknown.
Solution for (a)
This part of the problem is limited to conditions just before the car is released and just after it leaves the spring. Take the initial height to be zero, so that both \(h_{\mathrm{i}}\) and \(h_{\mathrm{f}}\) are zero. Furthermore, the initial speed \(v_{\mathrm{i}}\) is zero and the final compression of the spring is zero, and so several terms in the conservation of mechanical energy equation are zero and it simplifies to
\[\mathrm{PE}_{\mathrm{si}}=\frac{1}{2} m v_{\mathrm{f}}^{2}. \nonumber\]
In other words, the initial potential energy in the spring is converted completely to kinetic energy in the absence of friction. Solving for the final speed and entering known values yields
\[v_{\mathrm{f}}=\sqrt{\frac{2 \mathrm{PE}_{\mathrm{si}}}{m}}=\sqrt{\frac{(2)(0.200 \mathrm{~J})}{0.100 \mathrm{~kg}}}=2.00 \mathrm{~m} / \mathrm{s}. \nonumber\]
Solution for (b)
One method of finding the speed at the top of the slope is to consider conditions just before the car is released and just after it reaches the top of the slope, completely ignoring everything in between. Doing the same type of analysis to find which terms are zero, the conservation of mechanical energy becomes
\[\mathrm{PE}_{\mathrm{si}}=\frac{1}{2} m v_{\mathrm{f}}^{2}+m g h_{\mathrm{f}}. \nonumber\]
This form of the equation means that the spring’s initial potential energy is converted partly to gravitational potential energy and partly to kinetic energy. The final speed at the top of the slope will be less than at the bottom. Solving for vfsize 12{v rSub { size 8{f} } } {} and substituting known values gives
\[v_{\mathrm{f}}=\sqrt{\frac{(2)\left(\mathrm{PE}_{\mathrm{si}}-m g h_{\mathrm{f}}\right)}{m}}=\sqrt{\frac{0.0472 \mathrm{~J}}{0.100 \mathrm{~kg}}}=0.687 \mathrm{~m} / \mathrm{s} \nonumber\]
Discussion
Another way to solve this problem is to realize that the car’s kinetic energy before it goes up the slope is converted partly to potential energy—that is, to take the final conditions in part (a) to be the initial conditions in part (b).
Note that, for conservative forces, we do not directly calculate the work they do; rather, we consider their effects through their corresponding potential energies, just as we did in Example \(\PageIndex{1}\). Note also that we do not consider details of the path taken—only the starting and ending points are important (as long as the path is not impossible). This assumption is usually a tremendous simplification, because the path may be complicated and forces may vary along the way.
Conservation of Total Energy
Energy, as we have noted, is conserved, making it one of the most important physical quantities in nature. The law of conservation of energy can be stated as follows:
Total energy is constant in any process. It may change in form or be transferred from one system to another, but the total remains the same.
We have explored some forms of energy and some ways it can be transferred from one system to another, in the case of work done by conservative forces transforming between potential energy and kinetic energy. Together, these make up the mechanical energy (KE+PE), and the mechanical energy is not always conserved, because it can be transformed into other forms of energy through work done by non-conservative forces. Here, we list some of the many forms energy can take.
Some of the Many Forms of Energy
Here are some of the many forms of energy. You probably have heard of some of these before; many of these will be covered in later chapters, but let us detail a few here. Electrical energy is a common form that is converted to many other forms and does work in a wide range of practical situations. Fuels, such as gasoline and food, carry chemical energy that can be transferred to a system through oxidation. Chemical fuel can also produce electrical energy, such as in batteries. Batteries can in turn produce light, which is a very pure form of energy. Most energy sources on Earth are in fact stored energy from the energy we receive from the Sun. We sometimes refer to this as radiant energy, or electromagnetic radiation, which includes visible light, infrared, and ultraviolet radiation. Nuclear energy comes from processes that convert measurable amounts of mass into energy. Nuclear energy is transformed into the energy of sunlight, into electrical energy in power plants, and into the energy of the heat transfer and blast in weapons. Atoms and molecules inside all objects are in random motion. This internal mechanical energy from the random motions is called thermal energy, because it is related to the temperature of the object. These and all other forms of energy can be converted into one another and can do work.
PROBLEM-SOLVING STRATEGIES FOR ENERGY PROBLEMS
You will find the following problem-solving strategies useful whenever you deal with energy. The strategies help in organizing and reinforcing energy concepts. In fact, they are used in the examples presented in this chapter. The familiar general problem-solving strategies presented earlier—involving identifying physical principles, knowns, and unknowns, checking units, and so on—continue to be relevant here.
Step 1. Determine the system of interest and identify what information is given and what quantity is to be calculated. A sketch will help.
Step 2. Examine all the forces involved and determine whether you know or are given the potential energy from the work done by the forces. Then use step 3 or step 4.
Step 3. If you know the potential energies for the forces that enter into the problem, then forces are all conservative, and you can apply conservation of mechanical energy simply in terms of potential and kinetic energy. Use \(\\mathrm{KE}_{\mathrm{i}}+\mathrm{PE}_{\mathrm{i}}=\mathrm{KE}_{\mathrm{f}}+\mathrm{PE}_{\mathrm{f}} \text {. }\) or \(\Delta \mathrm{KE}+\Delta \mathrm{PE}=0\) as starting point and use formulas for kinetic energy and potential energies.
Step 4. If you know that the total mechanical energy changes (usually there will be some hint of work done by non-conservative forces, energy input from other forms of energy, or even an explicit statement of how much work is done on the system, changing its total mechanical energy), then you can use the information given in the problem to say that, the change of total mechanical energy is due to these non-conservative forces: \(\Delta \mathrm{KE}+\Delta \mathrm{PE}=W_{\mathrm{nc}}\). Make sure \(W_{\mathrm{nc}}\) does not include work done by conservative forces, since those are already accounted for in the potential energy.
Step 5. You have already identified the types of work and energy involved (in step 2). Before solving for the unknown, eliminate terms wherever possible to simplify the algebra. For example, choose \(h=0\) at either the initial or final point, so that \(\mathrm{PE}_{\mathrm{g}}\) is zero there. Then solve for the unknown in the customary manner.
Step 6. Check the answer to see if it is reasonable. Once you have solved a problem, reexamine the forms of work and energy to see if you have set up the conservation of energy equation correctly. For example, work done against friction should be negative, potential energy at the bottom of a hill should be less than that at the top, and so on. Also check to see that the numerical value obtained is reasonable. For example, the final speed of a skateboarder who coasts down a 3-m-high ramp could reasonably be 20 km/h, but not 80 km/h.
Transformation of Energy
The transformation of energy from one form into others is happening all the time. The chemical energy in food is converted into thermal energy through metabolism; light energy is converted into chemical energy through photosynthesis. In a larger example, the chemical energy contained in coal is converted into thermal energy as it burns to turn water into steam in a boiler. This thermal energy in the steam in turn is converted to mechanical energy as it spins a turbine, which is connected to a generator to produce electrical energy. (In all of these examples, not all of the initial energy is converted into the forms mentioned. This important point is discussed later in this section.)
Another example of energy conversion occurs in a solar cell. Sunlight impinging on a solar cell (see Figure \(\PageIndex{2}\)) produces electricity, which in turn can be used to run an electric motor. Energy is converted from the primary source of solar energy into electrical energy and then into mechanical energy.
Section Summary
- A conservative force is one for which work depends only on the starting and ending points of a motion, not on the path taken.
- We can define potential energy (PE) for any conservative force, just as we defined \(\mathrm{PE}_{\mathrm{g}}\) for the gravitational force.
- Mechanical energy is defined to be KE+PE for a conservative force.
- When only conservative forces act on and within a system, the total mechanical energy is conserved, \(\Delta \mathrm{KE}+\Delta \mathrm{PE}=0\).
- The law of conservation of energy states that the total energy, including the mechanical energy and other forms of energy, is constant in any process. Energy may change in form or be transferred from one system to another, but the total remains the same.
- Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy.
Glossary
- conservative force
- a force that is a function of position alone, with the result that the work done by the force depends only on the starting and ending points of a motion and not on the particular path taken
- potential energy
- energy due to position, shape, or configuration
- conservation of mechanical energy
- the rule that the sum of the kinetic energies and potential energies remains constant if only conservative forces act on and within a system
- mechanical energy
- the sum of kinetic energy and potential energy
- law of conservation of energy
- the general law that total energy is constant in any process; energy may change in form or be transferred from one system to another, but the total remains the same
- electrical energy
- the energy carried by a flow of charge
- chemical energy
- the energy in a substance stored in the bonds between atoms and molecules that can be released in a chemical reaction
- radiant energy
- the energy carried by electromagnetic waves
- nuclear energy
- energy released by changes within atomic nuclei, such as the fusion of two light nuclei or the fission of a heavy nucleus
- thermal energy
- the energy within an object due to the random motion of its atoms and molecules that accounts for the object's temperature