14.E: Nuclear and Particle Physics (Exercise)
- Page ID
- 56598
Conceptual Questions
15.1: Nuclear Radioactivity
1. Suppose the range for \(5.0 ~\mathrm{MeV} \alpha\) ray is known to be 2.0 mm in a certain material. Does this mean that every \(5.0 ~\mathrm{MeV} \alpha\) a ray that strikes this material travels 2.0 mm, or does the range have an average value with some statistical fluctuations in the distances traveled? Explain.
2. What is the difference between \(\gamma\) rays and characteristic X-rays? Is either necessarily more energetic than the other? Which can be the most energetic?
3. Ionizing radiation interacts with matter by scattering from electrons and nuclei in the substance. Based on the law of conservation of momentum and energy, explain why electrons tend to absorb more energy than nuclei in these interactions.
4. What characteristics of radioactivity show it to be nuclear in origin and not atomic?
5. What is the source of the energy emitted in radioactive decay? Identify an earlier conservation law, and describe how it was modified to take such processes into account.
6. Consider the figure. If an electric field is substituted for the magnetic field with positive charge instead of the north pole and negative charge instead of the south pole, in which directions will the \(\alpha\), \(\beta\) , and \(\gamma\) rays bend?
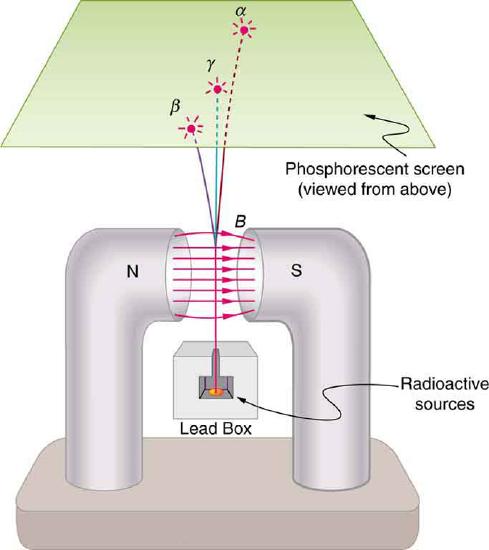
7. Explain how an \(\alpha\) particle can have a larger range in air than a \(\beta\) particle with the same energy in lead.
8. Arrange the following according to their ability to act as radiation shields, with the best first and worst last. Explain your ordering in terms of how radiation loses its energy in matter.
(a) A solid material with low density composed of low-mass atoms.
(b) A gas composed of high-mass atoms.
(c) A gas composed of low-mass atoms.
(d) A solid with high density composed of high-mass atoms.
9. Often, when people have to work around radioactive materials spills, we see them wearing white coveralls (usually a plastic material). What types of radiation (if any) do you think these suits protect the worker from, and how?
15.2: Radiation Detection and Detectors
10. Is it possible for light emitted by a scintillator to be too low in frequency to be used in a photomultiplier tube? Explain.
15.3: Substructure of the Nucleus
11. The weak and strong nuclear forces are basic to the structure of matter. Why we do not experience them directly?
12. Define and make clear distinctions between the terms neutron, nucleon, nucleus, nuclide, and neutrino.
13. What are isotopes? Why do different isotopes of the same element have similar chemistries?
15.4: Nuclear Decay and Conservation Laws
14. Star Trek fans have often heard the term “antimatter drive.” Describe how you could use a magnetic field to trap antimatter, such as produced by nuclear decay, and later combine it with matter to produce energy. Be specific about the type of antimatter, the need for vacuum storage, and the fraction of matter converted into energy.
15. What conservation law requires an electron’s neutrino to be produced in electron capture? Note that the electron no longer exists after it is captured by the nucleus.
16. Neutrinos are experimentally determined to have an extremely small mass. Huge numbers of neutrinos are created in a supernova at the same time as massive amounts of light are first produced. When the 1987A supernova occurred in the Large Magellanic Cloud, visible primarily in the Southern Hemisphere and some 100,000 light-years away from Earth, neutrinos from the explosion were observed at about the same time as the light from the blast. How could the relative arrival times of neutrinos and light be used to place limits on the mass of neutrinos?
17. What do the three types of beta decay have in common that is distinctly different from alpha decay?
15.5: Half-Life and Activity
18. In a \(3 \times 10^{9}\)-year-old rock that originally contained some \({ }^{238} \mathrm{U}\), which has a half-life of \(4.5 \times 10^{9}\) years, we expect to find some \({ }^{238} \mathrm{U}\) remaining in it. Why are \({ }^{226} \mathrm{Ra}\), \({ }^{222} \mathrm{Rn}\), and \({ }^{210} \mathrm{Po}\) also found in such a rock, even though they have much shorter half-lives (1600 years, 3.8 days, and 138 days, respectively)?
19. Does the number of radioactive nuclei in a sample decrease to exactly half its original value in one half-life? Explain in terms of the statistical nature of radioactive decay.
20. Radioactivity depends on the nucleus and not the atom or its chemical state. Why, then, is one kilogram of uranium more radioactive than one kilogram of uranium hexafluoride?
21. Explain how a bound system can have less mass than its components. Why is this not observed classically, say for a building made of bricks?
22. Spontaneous radioactive decay occurs only when the decay products have less mass than the parent, and it tends to produce a daughter that is more stable than the parent. Explain how this is related to the fact that more tightly bound nuclei are more stable. (Consider the binding energy per nucleon.)
23. To obtain the most precise value of BE from the equation \(\mathrm{BE}=\left[Z M\left({ }^{1} \mathrm{H}\right)+N m_{n}\right] c^{2}-m\left({ }^{A} \mathrm{X}\right) c^{2}\), we should take into account the binding energy of the electrons in the neutral atoms. Will doing this produce a larger or smaller value for BE? Why is this effect usually negligible?
24. How does the finite range of the nuclear force relate to the fact that \(\mathrm{BE} / A\) is greatest for \(A\) near 60?
15.6: Medical Imaging and Diagnostics
25. In terms of radiation dose, what is the major difference between medical diagnostic uses of radiation and medical therapeutic uses?
26. One of the methods used to limit radiation dose to the patient in medical imaging is to employ isotopes with short half-lives. How would this limit the dose?
15.7: Biological Effects of Ionizing Radiation
27. Isotopes that emit \(\alpha\) radiation are relatively safe outside the body and exceptionally hazardous inside. Yet those that emit \(\gamma\) radiation are hazardous outside and inside. Explain why.
28. Why is radon more closely associated with inducing lung cancer than other types of cancer?
29. The RBE for low-energy \(\beta\)s is 1.7, whereas that for higher-energy \(\beta\)s is only 1. Explain why, considering how the range of radiation depends on its energy.
30. Which methods of radiation protection were used in the device shown in the first photo in the figure? Which were used in the situation shown in the second photo?
(a)
31. What radioisotope could be a problem in homes built of cinder blocks made from uranium mine tailings? (This is true of homes and schools in certain regions near uranium mines.)
32. Are some types of cancer more sensitive to radiation than others? If so, what makes them more sensitive?
33. Suppose a person swallows some radioactive material by accident. What information is needed to be able to assess possible damage?
15.8: Fusion
34. Why does the fusion of light nuclei into heavier nuclei release energy?
35. Energy input is required to fuse medium-mass nuclei, such as iron or cobalt, into more massive nuclei. Explain why.
36. In considering potential fusion reactions, what is the advantage of the reaction \({ }^{2} \mathrm{H}+{ }^{3} \mathrm{H} \rightarrow{ }^{4} \mathrm{He}+n\) over the reaction \({ }^{2} \mathrm{H}+{ }^{2} \mathrm{H} \rightarrow{ }^{3} \mathrm{He}+n\)?
37. Give reasons justifying the contention made in the text that energy from the fusion reaction \({ }^{2} \mathrm{H}+{ }^{2} \mathrm{H} \rightarrow{ }^{4} \mathrm{He}+\gamma\) is relatively difficult to capture and utilize.
15.9: Fission
38. Explain why the fission of heavy nuclei releases energy. Similarly, why is it that energy input is required to fission light nuclei?
39. Explain, in terms of conservation of momentum and energy, why collisions of neutrons with protons will thermalize neutrons better than collisions with oxygen.
40. The ruins of the Chernobyl reactor are enclosed in a huge concrete structure built around it after the accident. Some rain penetrates the building in winter, and radioactivity from the building increases. What does this imply is happening inside?
41. Since the uranium or plutonium nucleus fissions into several fission fragments whose mass distribution covers a wide range of pieces, would you expect more residual radioactivity from fission than fusion? Explain.
42. The core of a nuclear reactor generates a large amount of thermal energy from the decay of fission products, even when the power-producing fission chain reaction is turned off. Would this residual heat be greatest after the reactor has run for a long time or short time? What if the reactor has been shut down for months?
43. How can a nuclear reactor contain many critical masses and not go supercritical? What methods are used to control the fission in the reactor?
44. Why can heavy nuclei with odd numbers of neutrons be induced to fission with thermal neutrons, whereas those with even numbers of neutrons require more energy input to induce fission?
45. Why is a conventional fission nuclear reactor not able to explode as a bomb?
15.10: Nuclear Weapons
46. What are some of the reasons that plutonium rather than uranium is used in all fission bombs and as the trigger in all fusion bombs?
47. Use the laws of conservation of momentum and energy to explain how a shape charge can direct most of the energy released in an explosion in a specific direction. (Note that this is similar to the situation in guns and cannons—most of the energy goes into the bullet.)
48. How does the lithium deuteride in the thermonuclear bomb shown in the figure supply tritium (\({ }^{3} \mathrm{H}\)) as well as deuterium (\({ }^{2} \mathrm{H}\))?
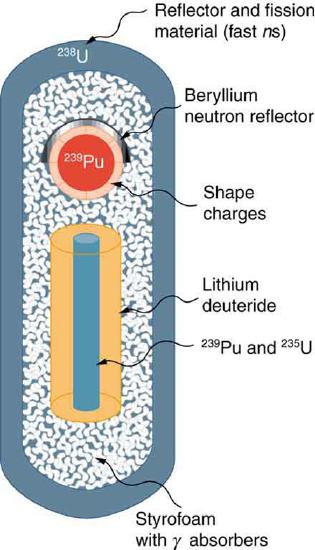
49. Fallout from nuclear weapons tests in the atmosphere is mainly \({ }^{90} \mathrm{Sr}\) and \({ }^{137} \mathrm{Cs}\), which have 28.6- and 32.2-y half-lives, respectively. Atmospheric tests were terminated in most countries in 1963, although China only did so in 1980. It has been found that environmental activities of these two isotopes are decreasing faster than their half-lives. Why might this be?
15.12: Particles, Patterns, and Conservation Laws
50. Large quantities of antimatter isolated from normal matter should behave exactly like normal matter. An antiatom, for example, composed of positrons, antiprotons, and antineutrons should have the same atomic spectrum as its matter counterpart. Would you be able to tell it is antimatter by its emission of antiphotons? Explain briefly.
51. Massless particles are not only neutral, they are chargeless (unlike the neutron). Why is this so?
52. Massless particles must travel at the speed of light, while others cannot reach this speed. Why are all massless particles stable? If evidence is found that neutrinos spontaneously decay into other particles, would this imply they have mass?
53. When a star erupts in a supernova explosion, huge numbers of electron neutrinos are formed in nuclear reactions. Such neutrinos from the 1987A supernova in the relatively nearby Magellanic Cloud were observed within hours of the initial brightening, indicating they traveled to earth at approximately the speed of light. Explain how this data can be used to set an upper limit on the mass of the neutrino, noting that if the mass is small the neutrinos could travel very close to the speed of light and have a reasonable energy (on the order of MeV).
54. Theorists have had spectacular success in predicting previously unknown particles. Considering past theoretical triumphs, why should we bother to perform experiments?
55. What lifetime do you expect for an antineutron isolated from normal matter?
56. Why does the \(\eta^{0}\) meson have such a short lifetime compared to most other mesons?
57. (a) Is a hadron always a baryon?
(b) Is a baryon always a hadron?
(c) Can an unstable baryon decay into a meson, leaving no other baryon?
58. Explain how conservation of baryon number is responsible for conservation of total atomic mass (total number of nucleons) in nuclear decay and reactions.
15.13: GUTs- The Unification of Forces
59. If a GUT is proven, and the four forces are unified, it will still be correct to say that the orbit of the moon is determined by the gravitational force. Explain why.
60. If the Higgs boson is discovered and found to have mass, will it be considered the ultimate carrier of the weak force? Explain your response.
61. Gluons and the photon are massless. Does this imply that the \(W^{+}\), \(W^{-}\), and \(Z^{0}\) are the ultimate carriers of the weak force?
Problems & Exercises
15.2: Radiation Detection and Detectors
62. The energy of 30.0 eV is required to ionize a molecule of the gas inside a Geiger tube, thereby producing an ion pair. Suppose a particle of ionizing radiation deposits 0.500 MeV of energy in this Geiger tube. What maximum number of ion pairs can it create?
Solution
1.67×104
63. A particle of ionizing radiation creates 4000 ion pairs in the gas inside a Geiger tube as it passes through. What minimum energy was deposited, if 30.0 eV is required to create each ion pair?
64. (a) Repeat Exercise 15.2.63, and convert the energy to joules or calories. (b) If all of this energy is converted to thermal energy in the gas, what is its temperature increase, assuming 50.0 cm3 of ideal gas at 0.250-atm pressure? (The small answer is consistent with the fact that the energy is large on a quantum mechanical scale but small on a macroscopic scale.)
65. Suppose a particle of ionizing radiation deposits 1.0 MeV in the gas of a Geiger tube, all of which goes to creating ion pairs. Each ion pair requires 30.0 eV of energy. (a) The applied voltage sweeps the ions out of the gas in 1.00μs. What is the current? (b) This current is smaller than the actual current since the applied voltage in the Geiger tube accelerates the separated ions, which then create other ion pairs in subsequent collisions. What is the current if this last effect multiplies the number of ion pairs by 900?
15.3: Substructure of the Nucleus
66. Verify that a \(2.3 \times 10^{17} \mathrm{~kg}\) mass of water at normal density would make a cube 60 km on a side, as claimed in Example 15.3.1. (This mass at nuclear density would make a cube 1.0 m on a side.)
Solution
\[\begin{aligned}
m=\rho V=\rho d^{3} & \Rightarrow a=\left(\frac{m}{\rho}\right)^{1 / 3}=\left(\frac{2.3 \times 10^{17} \mathrm{~kg}}{1000 \mathrm{~kg} / \mathrm{m}^{3}}\right)^{\frac{1}{3}} \\
&=61 \times 10^{3} \mathrm{~m}=61 \mathrm{~km}
\end{aligned} \nonumber\]
67. Find the length of a side of a cube having a mass of 1.0 kg and the density of nuclear matter, taking this to be \(2.3 \times 10^{17} \mathrm{~kg} / \mathrm{m}^{3}\).
68. What is the radius of an \(\alpha\) particle?
Solution
1.9 fm
69. Find the radius of a \({ }^{238} \mathrm{Pu}\) nucleus. \({ }^{238} \mathrm{Pu}\) is a manufactured nuclide that is used as a power source on some space probes.
(a) Calculate the radius of \({ }^{58} \mathrm{Ni}\), one of the most tightly bound stable nuclei.
(b) What is the ratio of the radius of \({ }^{58} \mathrm{Ni}\) to that of \({ }^{258} \mathrm{Ha}\), one of the largest nuclei ever made? Note that the radius of the largest nucleus is still much smaller than the size of an atom.
Solution
(a) 4.6 fm
(b) 0.61 to 1
70. The unified atomic mass unit is defined to be \(1 \mathrm{u}=1.6605 \times 10^{-27} \mathrm{~kg}\). Verify that this amount of mass converted to energy yields 931.5 MeV. Note that you must use four-digit or better values for \(c\) and \(\left|q_{e}\right|\).
71. What is the ratio of the velocity of a \(\beta\) particle to that of an \(\alpha\) particle, if they have the same nonrelativistic kinetic energy?
Solution
85.4 to 1
72. If a 1.50-cm-thick piece of lead can absorb 90.0% of the \(\gamma\) rays from a radioactive source, how many centimeters of lead are needed to absorb all but 0.100% of the \(\gamma\) rays?
73. The detail observable using a probe is limited by its wavelength. Calculate the energy of a \(\gamma\)-ray photon that has a wavelength of \(1 \times 10^{-16} \mathrm{~m}\), small enough to detect details about one-tenth the size of a nucleon. Note that a photon having this energy is difficult to produce and interacts poorly with the nucleus, limiting the practicability of this probe.
Solution
12.4 GeV
74. (a) Show that if you assume the average nucleus is spherical with a radius \(r=r_{0} A^{1 / 3}\), and with a mass of \(A\) u, then its density is independent of \(A\).
(b) Calculate that density in \(\mathrm{u} / \mathrm{fm}^{3}\) and \(\mathrm{kg} / \mathrm{m}^{3}\), and compare your results with those found in Example 15.3.1 for \({ }^{56} \mathrm{Fe}\).
75. What is the ratio of the velocity of a 5.00-MeV \(\beta\) ray to that of an \(\alpha\) particle with the same kinetic energy? This should confirm that \(\beta\)s travel much faster than \(\alpha\)s even when relativity is taken into consideration. (See also Exercise 15.3.71.)
Solution
19.3 to 1
15.4: Nuclear Decay and Conservation Laws
In the following eight problems, write the complete decay equation for the given nuclide in the complete \({ }_{Z}^{A} \mathrm{X}_{N}\) notation. Refer to the periodic table for values of \(Z\).
76. \(\beta^{-}\) decay of \({ }^{3} \mathrm{H}\) (tritium), a manufactured isotope of hydrogen used in some digital watch displays, and manufactured primarily for use in hydrogen bombs.
Solution
\[{ }_{1}^{3} \mathrm{H}_{2} \rightarrow{ }_{2}^{3} \mathrm{He}_{1}+\beta^{-}+\bar{\nu}_{e} \nonumber\]
77. \(\beta^{-}\) decay of \({ }^{40} \mathrm{K}\), a naturally occurring rare isotope of potassium responsible for some of our exposure to background radiation.
78. \(\beta^{+}\) decay of \({ }^{50} \mathrm{Mn}\).
Solution
\[{ }_{25}^{50} M_{25} \rightarrow{ }_{24}^{50} \mathrm{Cr}_{26}+\beta^{+}+\nu_{e} \nonumber\]
79. \(\beta^{+}\) decay of \({ }^{52} \mathrm{Fe}\).
80. Electron capture by \({ }^{7} \mathrm{Be}\).
Solution
\[{ }_{4}^{7} \mathrm{Be}_{3}+e^{-} \rightarrow{ }_{3}^{7} \mathrm{Li}_{4}+\nu_{e} \nonumber\]
81. Electron capture by \({ }^{106} \mathrm{In}\).
82. \(\alpha\) decay of \({ }^{210} \mathrm{Po}\), the isotope of polonium in the decay series of \({ }^{238} \mathrm{~u}\) that was discovered by the Curies. A favorite isotope in physics labs, since it has a short half-life and decays to a stable nuclide.
Solution
\[{ }_{84}^{210} \mathrm{Po}_{126} \rightarrow{ }_{82}^{206} \mathrm{~Pb}_{124}+{ }_{2}^{4} \mathrm{He}_{2} \nonumber\]
83. \(\alpha\) decay of \({ }^{226} \mathrm{Ra}\), another isotope in the decay series of \({ }^{238} \mathrm{~u}\), first recognized as a new element by the Curies. Poses special problems because its daughter is a radioactive noble gas.
In the following four problems, identify the parent nuclide and write the complete decay equation in the \({ }_{Z}^{A} \mathrm{X}_{N}\) notation. Refer to the periodic table for values of \(Z\).
84. \(\beta^{-}\) decay producing \({ }^{137} \mathrm{Ba}\). The parent nuclide is a major waste product of reactors and has chemistry similar to potassium and sodium, resulting in its concentration in your cells if ingested.
Solution
\[{ }_{55}^{137} \mathrm{Cs}_{82} \rightarrow{ }_{56}^{137} \mathrm{Ba}_{81}+\beta^{-}+\bar{\nu}_{e} \nonumber\]
85. \(\beta^{-}\) decay producing \({ }^{90} \mathrm{Y}\). The parent nuclide is a major waste product of reactors and has chemistry similar to calcium, so that it is concentrated in bones if ingested (\({ }^{90} \mathrm{Y}\) is also radioactive.)
86. \(\alpha\) decay producing \({ }^{228} \mathrm{Ra}\). The parent nuclide is nearly 100% of the natural element and is found in gas lantern mantles and in metal alloys used in jets (\({ }^{228} \mathrm{Ra}\) is also radioactive).
Solution
\[{ }_{90}^{232} \mathrm{Th}_{142} \rightarrow{ }_{88}^{228} \mathrm{Ra}_{140}+{ }_{2}^{4} \mathrm{He}_{2} \nonumber\]
87. \(\alpha\) decay producing \({ }^{208} \mathrm{Pb}\). The parent nuclide is in the decay series produced by \({ }^{232} \mathrm{Th}\), the only naturally occurring isotope of thorium.
88. When an electron and positron annihilate, both their masses are destroyed, creating two equal energy photons to preserve momentum.
(a) Confirm that the annihilation equation \(e^{+}+e^{-} \rightarrow \gamma+\gamma\) conserves charge, electron family number, and total number of nucleons. To do this, identify the values of each before and after the annihilation.
(b) Find the energy of each \(\gamma\) ray, assuming the electron and positron are initially nearly at rest.
(c) Explain why the two \(\gamma\) rays travel in exactly opposite directions if the center of mass of the electron-positron system is initially at rest.
Solution
(a) charge:(+1) + (−1) = 0; electron family number: (+1) + (−1) = 0; A: 0 + 0 = 0
(b) 0.511 MeV
(c) The two \(\gamma\) rays must travel in exactly opposite directions in order to conserve momentum, since initially there is zero momentum if the center of mass is initially at rest.
89. Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for \(\alpha\) decay given in the equation \({ }_{Z}^{A} \mathrm{X}_{N} \rightarrow{ }_{Z-2}^{A-4} \mathrm{Y}_{N-2}+{ }_{2}^{4} \mathrm{He}_{2}\). To do this, identify the values of each before and after the decay.
90. Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for \(\beta^{-}\) decay given in the equation \({ }_{Z}^{A} \mathrm{X}_{N} \rightarrow{ }_{Z+1}^{A} \mathrm{Y}_{N-1}+\beta^{-}+\bar{\nu}_{e}\). To do this, identify the values of each before and after the decay.
Solution
Z = (Z+1) − 1 ; A = A; efn : 0 = (+1) + (−1)
91. Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for \(\beta^{-}\) decay given in the equation \({ }_{Z}^{A} \mathrm{X}_{N} \rightarrow{ }_{Z-1}^{A} \mathrm{Y}_{N-1}+\beta^{-}+\nu_{e}\). To do this, identify the values of each before and after the decay.
92. Confirm that charge, electron family number, and the total number of nucleons are all conserved by the rule for electron capture given in the equation \({ }_{Z}^{A} \mathrm{X}_{N}+e^{-} \rightarrow{ }_{Z-1}^{A} \mathrm{Y}_{N+1}+\nu_{e}\). To do this, identify the values of each before and after the capture.
Solution
Z − 1 = Z − 1 ; A = A ; efn : (+1) = (+1)
93. A rare decay mode has been observed in which \({ }^{222} \mathrm{Ra}\) emits a \({ }^{14} \mathrm{C}\) nucleus.
(a) The decay equation is \({ }^{222} \mathrm{Ra} \rightarrow{ }^{A} \mathrm{X}+{ }^{14} \mathrm{C}\). Identify the nuclide \({ }^{A} \mathrm{X}\).
(b) Find the energy emitted in the decay. The mass of \({ }^{222} \mathrm{Ra}\) is 222.015353 u.
94. (a) Write the complete \(\alpha\) decay equation for \({ }^{226} \mathrm{Ra}\).
(b) Find the energy released in the decay.
Solution
(a) \({ }_{88}^{226} \mathrm{Ra}_{138} \rightarrow{ }_{86}^{222} \mathrm{Rn}_{136}+{ }_{2}^{4} \mathrm{He}_{2}\)
(b) 4.87 MeV
95. (a) Write the complete \(\alpha\) decay equation for \({ }^{249} \mathrm{Cf}\).
(b) Find the energy released in the decay.
96. (a) Write the complete \(\beta^{-}\) decay equation for the neutron.
(b) Find the energy released in the decay.
Solution
(a) \(\mathrm{n} \rightarrow \mathrm{p}+\beta^{-}+\bar{\nu}_{e}\)
(b) ) 0.783 MeV
97. (a) Write the complete \(\beta^{-}\) decay equation for \({ }^{90} \mathrm{Sr}\), a major waste product of nuclear reactors.
(b) Find the energy released in the decay.
98. Calculate the energy released in the \(\beta^{+}\) decay of \({ }^{22} \mathrm{Na}\), the equation for which is given in the text. The masses of \({ }^{22} \mathrm{Na}\) and \({ }^{22} \mathrm{Ne}\) are 21.994434 and 21.991383 u, respectively.
Solution
1.82 MeV
99. (a) Write the complete \(\beta^{+}\) decay equation for \({ }^{11} \mathrm{C}\).
(b) Calculate the energy released in the decay. The masses of \({ }^{11} \mathrm{C}\) and \({ }^{11} \mathrm{B}\) are 11.011433 and 11.009305 u, respectively.
100. (a) Calculate the energy released in the \(\alpha\) decay of \({ }^{238} \mathrm{~u}\).
(b) What fraction of the mass of a single \({ }^{238} \mathrm{~u}\) is destroyed in the decay? The mass of \({ }^{234} \mathrm{Th}\) is 234.043593 u.
(c) Although the fractional mass loss is large for a single nucleus, it is difficult to observe for an entire macroscopic sample of uranium. Why is this?
Solution
(a) 4.274 MeV
(b) \(1.927 \times 10^{-5}\)
(c) Since U-238 is a slowly decaying substance, only a very small number of nuclei decay on human timescales; therefore, although those nuclei that decay lose a noticeable fraction of their mass, the change in the total mass of the sample is not detectable for a macroscopic sample.
101. (a) Write the complete reaction equation for electron capture by \({ }^{7} \mathrm{Be}\).
(b) Calculate the energy released.
102. (a) Write the complete reaction equation for electron capture by \({ }^{15} \mathrm{O}\).
(b) Calculate the energy released.
Solution
(a) \({ }_{8}^{15} \mathrm{O}_{7}+e^{-} \rightarrow{ }_{7}^{15} \mathrm{~N}_{8}+\nu_{e}\)
(b) 2.754 MeV
15.5: Half-Life and Activity
103. Data from the appendices and the periodic table may be needed for these problems.
104. An old campfire is uncovered during an archaeological dig. Its charcoal is found to contain less than 1/1000 the normal amount of \({ }^{14} \mathrm{C}\). Estimate the minimum age of the charcoal, noting that \(2^{10}=1024\).
Solution
57,300 y
105. A \({ }^{60} \mathrm{Co}\) source is labeled 4.00 mCi, but its present activity is found to be \(1.85 \times 10^{7}\) Bq. (a) What is the present activity in mCi? (b) How long ago did it actually have a 4.00-mCi activity?
106. (a) Calculate the activity \(R\) in curies of 1.00 g of \({ }^{226} \mathrm{Ra}\).
(b) Discuss why your answer is not exactly 1.00 Ci, given that the curie was originally supposed to be exactly the activity of a gram of radium.
Solution
(a) 0.988 Ci
(b) The half-life of \({ }^{226} \mathrm{Ra}\) is now better known.
107. Show that the activity of the \({ }^{14} \mathrm{C}\) in 1.00 g of \({ }^{12} \mathrm{C}\) found in living tissue is 0.250 Bq.
108. Mantles for gas lanterns contain thorium, because it forms an oxide that can survive being heated to incandescence for long periods of time. Natural thorium is almost 100% \({ }^{232} \mathrm{Th}\), with a half-life of \(1.405 \times 10^{10} \mathrm{~y}\). If an average lantern mantle contains 300 mg of thorium, what is its activity?
Solution
\(1.22 \times 10^{3} \mathrm{~Bq}\)
109. Cow’s milk produced near nuclear reactors can be tested for as little as 1.00 pCi of \({ }^{131} \mathrm{I}\) per liter, to check for possible reactor leakage. What mass of \({ }^{131} \mathrm{I}\) has this activity?
110. (a) Natural potassium contains \({ }^{40} \mathrm{K}\), which has a half-life of \(1.277 \times 10^{9}\) y. What mass of \({ }^{40} \mathrm{K}\) in a person would have a decay rate of 4140 Bq? (b) What is the fraction of \({ }^{40} \mathrm{K}\) in natural potassium, given that the person has 140 g in his body? (These numbers are typical for a 70-kg adult.)
Solution
(a) 16.0 mg
(b) 0.0114%
111. There is more than one isotope of natural uranium. If a researcher isolates 1.00 mg of the relatively scarce \({ }^{235} \mathrm{U}\) and finds this mass to have an activity of 80.0 Bq, what is its half-life in years?
112. \({ }^{50} \mathrm{V}\) has one of the longest known radioactive half-lives. In a difficult experiment, a researcher found that the activity of 1.00 kg of \({ }^{50} \mathrm{V}\) is 1.75 Bq. What is the half-life in years?
Solution
\(1.48 \times 10^{17} \mathrm{~y}\)
113. You can sometimes find deep red crystal vases in antique stores, called uranium glass because their color was produced by doping the glass with uranium. Look up the natural isotopes of uranium and their half-lives, and calculate the activity of such a vase assuming it has 2.00 g of uranium in it. Neglect the activity of any daughter nuclides.
114. A tree falls in a forest. How many years must pass before the \({ }^{14} \mathrm{C}\) activity in 1.00 g of the tree’s carbon drops to 1.00 decay per hour?
Solution
\(5.6 \times 10^{4} \mathrm{~y}\)
115. What fraction of the \({ }^{40} \mathrm{K}\) that was on Earth when it formed \(4.5 \times 10^{9}\) years ago is left today?
116. A 5000-Ci \({ }^{60} \mathrm{Co}\) source used for cancer therapy is considered too weak to be useful when its activity falls to 3500 Ci. How long after its manufacture does this happen?
Solution
2.71 y
117. Natural uranium is 0.7200% \({ }^{235} \mathrm{U}\) and 99.27% \({ }^{238} \mathrm{U}\). What were the percentages of \({ }^{235} \mathrm{U}\) and \({ }^{238} \mathrm{U}\) in natural uranium when Earth formed \(4.5 \times 10^{9}\) years ago?
118. The \(\beta^{-}\) particles emitted in the decay of \({ }^{3} \mathrm{H}\) (tritium) interact with matter to create light in a glow-in-the-dark exit sign. At the time of manufacture, such a sign contains 15.0 Ci of \({ }^{3} \mathrm{H}\).
(a) What is the mass of the tritium?
(b) What is its activity 5.00 y after manufacture?
Solution
(a) 1.56 mg
(b) 11.3 Ci
119. World War II aircraft had instruments with glowing radium-painted dials. The activity of one such instrument was \(1.0 \times 10^{5}\) Bq when new.
(a) What mass of \({ }^{226} \mathrm{Ra}\) was present?
(b) After some years, the phosphors on the dials deteriorated chemically, but the radium did not escape. What is the activity of this instrument 57.0 years after it was made?
120. (a) The \({ }^{210} \mathrm{Po}\) source used in a physics laboratory is labeled as having an activity of \(1.0 \mu \mathrm{~Ci}\) on the date it was prepared. A student measures the radioactivity of this source with a Geiger counter and observes 1500 counts per minute. She notices that the source was prepared 120 days before her lab. What fraction of the decays is she observing with her apparatus?
(b) Identify some of the reasons that only a fraction of the \(\alpha\) s emitted are observed by the detector.
Solution
(a) \(1.23 \times 10^{-3}\)
(b) Only part of the emitted radiation goes in the direction of the detector. Only a fraction of that causes a response in the detector. Some of the emitted radiation (mostly \(\alpha\) particles) is observed within the source. Some is absorbed within the source, some is absorbed by the detector, and some does not penetrate the detector.
121. Armor-piercing shells with depleted uranium cores are fired by aircraft at tanks. (The high density of the uranium makes them effective.) The uranium is called depleted because it has had its \({ }^{235} \mathrm{U}\) removed for reactor use and is nearly pure \({ }^{238} \mathrm{U}\). Depleted uranium has been erroneously called non-radioactive. To demonstrate that this is wrong:
(a) Calculate the activity of 60.0 g of pure \({ }^{238} \mathrm{U}\).
(b) Calculate the activity of 60.0 g of natural uranium, neglecting the \({ }^{234} \mathrm{U}\) and all daughter nuclides.
122. The ceramic glaze on a red-orange Fiestaware plate is \(\mathrm{U}_{2} \mathrm{O}_{3}\) and contains 50.0 grams of \({ }^{238} \mathrm{U}\) , but very little \({ }^{235} \mathrm{U}\).
(a) What is the activity of the plate?
(b) Calculate the total energy that will be released by the \({ }^{238} \mathrm{U}\) decay.
(c) If energy is worth 12.0 cents per \(\mathrm{kW} \cdot \mathrm{h}\), what is the monetary value of the energy emitted? (These plates went out of production some 30 years ago, but are still available as collectibles.)
Solution
(a) \(1.68 \times 10^{-5} \mathrm{~Ci}\)
(b) \(8.65 \times 10^{10} \mathrm{~J}\)
(c) \(\$ 2.9 \times 10^{3}\)
123. Large amounts of depleted uranium (\({ }^{238} \mathrm{U}\)) are available as a by-product of uranium processing for reactor fuel and weapons. Uranium is very dense and makes good counter weights for aircraft. Suppose you have a 4000-kg block of \({ }^{238} \mathrm{U}\).
(a) Find its activity.
(b) How many calories per day are generated by thermalization of the decay energy?
(c) Do you think you could detect this as heat? Explain.
124. The Galileo space probe was launched on its long journey past several planets in 1989, with an ultimate goal of Jupiter. Its power source is 11.0 kg of \({ }^{238} \mathrm{Pu}\), a by-product of nuclear weapons plutonium production. Electrical energy is generated thermoelectrically from the heat produced when the 5.59-MeV \(\alpha\) particles emitted in each decay crash to a halt inside the plutonium and its shielding. The half-life of \({ }^{238} \mathrm{Pu}\) is 87.7 years.
(a) What was the original activity of the \({ }^{238} \mathrm{Pu}\) in becquerel?
(b) What power was emitted in kilowatts?
(c) What power was emitted 12.0 y after launch? You may neglect any extra energy from daughter nuclides and any losses from escaping \(\gamma\) rays.
Solution
(a) \(6.97 \times 10^{15} \mathrm{~Bq}\)
(b) 6.24 kW
(c) 5.67 kW
15.6: Medical Imaging and Diagnostics
125. A neutron generator uses an \(\alpha\) source, such as radium, to bombard beryllium, inducing the reaction \({ }^{4} \mathrm{He}+{ }^{9} \mathrm{Be} \rightarrow{ }^{12} \mathrm{C}+n\). Such neutron sources are called RaBe sources, or PuBe sources if they use plutonium to get the \(\alpha\) s. Calculate the energy output of the reaction in MeV.
Solution
5.701 MeV
126. Neutrons from a source (perhaps the one discussed in the preceding problem) bombard natural molybdenum, which is 24 percent \({ }^{98} \mathrm{Mo}\). What is the energy output of the reaction \({ }^{98} \mathrm{Mo}+n \rightarrow{ }^{99} \mathrm{Mo}+\gamma\)? The mass of \({ }^{98} \mathrm{Mo}\) is given in Appendix A: Atomic Masses, and that of \({ }^{98} \mathrm{Mo}\) is 98.907711 u.
127. The purpose of producing \({ }^{98} \mathrm{Mo}\) (usually by neutron activation of natural molybdenum, as in the preceding problem) is to produce \({ }^{99 \mathrm{m}} \mathrm{Tc}\). Using the rules, verify that the \(\beta^{-}\) decay of \({ }^{98} \mathrm{Mo}\) produces \({ }^{99 \mathrm{m}} \mathrm{Tc}\). (Most \({ }^{99 \mathrm{m}} \mathrm{Tc}\) nuclei produced in this decay are left in a metastable excited state denoted \({ }^{99 \mathrm{m}} \mathrm{Tc}\).)
Solution
\({ }_{42}^{99} \mathrm{Mo}_{57} \rightarrow{ }_{43}^{99} \mathrm{Tc}_{56}+\beta^{-}+\bar{v}_{e}\)
128. The purpose of producing \({ }^{98} \mathrm{Mo}\) (usually by neutron activation of natural molybdenum, as in the preceding problem) is to produce \({ }^{99 \mathrm{m}} \mathrm{Tc}\). Using the rules, verify that the \(\beta^{-}\) decay of \({ }^{98} \mathrm{Mo}\) produces \({ }^{99 \mathrm{m}} \mathrm{Tc}\). (Most \({ }^{99 \mathrm{m}} \mathrm{Tc}\) nuclei produced in this decay are left in a metastable excited state denoted \({ }^{99 \mathrm{m}} \mathrm{Tc}\).)
Solution
\({ }_{42}^{99} \mathrm{Mo}_{57} \rightarrow{ }_{43}^{99} \mathrm{Tc}_{56}+\beta^{-}+\bar{v}_{e}\)
129. Table 15.16.1 indicates that 7.50 mCi of \({ }^{99 \mathrm{m}} \mathrm{Tc}\) is used in a brain scan. What is the mass of technetium?
Solution
\(1.43 \times 10^{-9} \mathrm{~g}\)
130. The activities of \({ }^{131} \mathrm{I}\) and \({ }^{123} \mathrm{I}\) used in thyroid scans are given in Table 15.16.1 to be \(50\) and \(70 ~\mu \mathrm{Ci}\), respectively. Find and compare the masses of \({ }^{131} \mathrm{I}\) and \({ }^{123} \mathrm{I}\) in such scans, given their respective half-lives are 8.04 d and 13.2 h. The masses are so small that the radioiodine is usually mixed with stable iodine as a carrier to ensure normal chemistry and distribution in the body.
131. (a) Neutron activation of sodium, which is 100% \({ }^{23} \mathrm{Na}\), produces \({ }^{24} \mathrm{Na}\), which is used in some heart scans, as seen in Table 15.16.1. The equation for the reaction is \({ }^{23} \mathrm{Na}+n \rightarrow{ }^{24} \mathrm{Na}+\gamma\). Find its energy output, given the mass of \({ }^{24} \mathrm{Na}\) is 23.990962 u.
(b) What mass of \({ }^{24} \mathrm{Na}\) produces the needed 5.0-mCi activity, given its half-life is 15.0 h?
Solution
(a) 6.958 MeV
(b) \(5.7 \times 10^{-10} \mathrm{~g}\)
15.7: Biological Effects of Ionizing Radiation
132. What is the dose in mSv for:
(a) a 0.1 Gy X-ray?
(b) 2.5 mGy of neutron exposure to the eye?
(c) 1.5 mGy of \(\alpha\) exposure?
Solution
(a) 100 mSv
(b) 80 mSv
(c) ~30 mSv
133. Find the radiation dose in Gy for:
(a) A 10-mSv fluoroscopic X-ray series.
(b) 50 mSv of skin exposure by an \(\alpha\) emitter.
(c) 160 mSv of \(\beta^{-}\) and \(\gamma\) rays from the \({ }^{40} \mathrm{K}\) in your body.
134. How many Gy of exposure is needed to give a cancerous tumor a dose of 40 Sv if it is exposed to \(\alpha\) activity?
Solution
~2 Gy
135. What is the dose in Sv in a cancer treatment that exposes the patient to 200 Gy of \(\gamma\) rays?
136. One half the \(\gamma\) rays from \({ }^{99 \mathrm{m}} \mathrm{Tc}\) are absorbed by a 0.170-mm-thick lead shielding. Half of the \(\gamma\) rays that pass through the first layer of lead are absorbed in a second layer of equal thickness. What thickness of lead will absorb all but one in 1000 of these \(\gamma\) rays?
Solution
1.69 mm
137. A plumber at a nuclear power plant receives a whole-body dose of 30 mSv in 15 minutes while repairing a crucial valve. Find the radiation-induced yearly risk of death from cancer and the chance of genetic defect from this maximum allowable exposure.
138. In the 1980s, the term picowave was used to describe food irradiation in order to overcome public resistance by playing on the well-known safety of microwave radiation. Find the energy in MeV of a photon having a wavelength of a picometer.
Solution
1.24 MeV
139. Find the mass of \({ }^{239} \mathrm{Pu}\) that has an activity of \(1.00 ~\mu \mathrm{Ci}\).
15.8: Fusion
140. Verify that the total number of nucleons, total charge, and electron family number are conserved for each of the fusion reactions in the proton-proton cycle in
\[\begin{gathered}
{ }^{1} \mathrm{H}+{ }^{1} \mathrm{H} \rightarrow{ }^{2} \mathrm{H}+e^{+}+v_{\mathrm{e}} \\[10pt]
{ }^{1} \mathrm{H}+{ }^{2} \mathrm{H} \rightarrow{ }^{3} \mathrm{He}+\gamma,
\end{gathered} \nonumber\]
and
\[{ }^{3} \mathrm{He}+{ }^{3} \mathrm{He} \rightarrow{ }^{4} \mathrm{He}+{ }^{1} \mathrm{H}+{ }^{1} \mathrm{H}. \nonumber\]
(List the value of each of the conserved quantities before and after each of the reactions.)
Solution
(a) \(A=1+1=2, Z=1+1=1+1, \text { efn }=0=-1+1\)
(b) \(A=1+2=3, Z=1+1=2, \text { efn }=0=0\)
(c) \(A=3+3=4+1+1, Z=2+2=2+1+1, \text { efn }=0=0\)
141. Calculate the energy output in each of the fusion reactions in the proton-proton cycle, and verify the values given in the above summary.
142. Show that the total energy released in the proton-proton cycle is 26.7 MeV, considering the overall effect in \({ }^{1} \mathrm{H}+{ }^{1} \mathrm{H} \rightarrow{ }^{2} \mathrm{H}+e^{+}+v_{\mathrm{e}}\), \({ }^{1} \mathrm{H}+{ }^{2} \mathrm{H} \rightarrow{ }^{3} \mathrm{He}+\gamma\), and \({ }^{3} \mathrm{He}+{ }^{3} \mathrm{He} \rightarrow{ }^{4} \mathrm{He}+{ }^{1} \mathrm{H}+{ }^{1} \mathrm{H}\) and being certain to include the annihilation energy.
Solution
\(\begin{aligned}
E &=\left(m_{\mathrm{i}}-m_{\mathrm{f}}\right) c^{2} \\
&=\left[4 m\left({ }^{1} \mathrm{H}\right)-m\left({ }^{4} \mathrm{He}\right)\right] c^{2} \\
&=[4(1.007825)-4.002603](931.5 \mathrm{~MeV}) \\
&=26.73 \mathrm{~MeV}
\end{aligned}\)
143. Verify by listing the number of nucleons, total charge, and electron family number before and after the cycle that these quantities are conserved in the overall proton-proton cycle in \(2 e^{-}+4^{1} \mathrm{H} \rightarrow{ }^{4} \mathrm{He}+2 v_{\mathrm{e}}+6 \gamma\).
144. The energy produced by the fusion of a 1.00-kg mixture of deuterium and tritium was found in Example "Calculating Energy and Power from Fusion". Approximately how many kilograms would be required to supply the annual energy use in the United States?
Solution
\(3.12 \times 10^{5} \mathrm{~kg}\)
145. Tritium is naturally rare, but can be produced by the reaction \(n+{ }^{2} \mathrm{H} \rightarrow{ }^{3} \mathrm{H}+\gamma\). How much energy in MeV is released in this neutron capture?
146. Two fusion reactions mentioned in the text are
\(n+{ }^{3} \mathrm{He} \rightarrow{ }^{4} \mathrm{He}+\gamma\)
and
\(n+{ }^{1} \mathrm{H} \rightarrow{ }^{2} \mathrm{H}+\gamma\)
Both reactions release energy, but the second also creates more fuel. Confirm that the energies produced in the reactions are 20.58 and 2.22 MeV, respectively. Comment on which product nuclide is most tightly bound, \({ }^{4} \mathrm{He}\) or \({ }^{2} \mathrm{H}\).
Solution
\(\begin{aligned}
E &=\left(m_{\mathrm{i}}-m_{\mathrm{f}}\right) c^{2} \\
E_{1} &=(1.008665+3.016030-4.002603)(931.5 \mathrm{~MeV}) \\
&=20.58 \mathrm{~MeV} \\
E_{2} &=(1.008665+1.007825-2.014102)(931.5 \mathrm{~MeV}) \\
&=2.224 \mathrm{~MeV}
\end{aligned}\)
\({ }^{4} \mathrm{He}\) is more tightly bound, since this reaction gives off more energy per nucleon.
147. (a) Calculate the number of grams of deuterium in an 80,000-L swimming pool, given deuterium is 0.0150% of natural hydrogen.
(b) Find the energy released in joules if this deuterium is fused via the reaction \({ }^{2} \mathrm{H}+{ }^{2} \mathrm{H} \rightarrow{ }^{3} \mathrm{He}+n\).
(c) Could the neutrons be used to create more energy?
(d) Discuss the amount of this type of energy in a swimming pool as compared to that in, say, a gallon of gasoline, also taking into consideration that water is far more abundant.
148. How many kilograms of water are needed to obtain the 198.8 mol of deuterium, assuming that deuterium is 0.01500% (by number) of natural hydrogen?
Solution
\(1.19 \times 10^{4} \mathrm{~kg}\)
149. The power output of the Sun is \(4 \times 10^{26} \mathrm{~W}\).
(a) If 90% of this is supplied by the proton-proton cycle, how many protons are consumed per second?
(b) How many neutrinos per second should there be per square meter at the Earth from this process? This huge number is indicative of how rarely a neutrino interacts, since large detectors observe very few per day.
150. Another set of reactions that result in the fusing of hydrogen into helium in the Sun and especially in hotter stars is called the carbon cycle. It is
\[\begin{aligned}
&{ }^{12} \mathrm{C}+{ }^{1} \mathrm{H} \rightarrow{ }^{13} \mathrm{~N}+\gamma, \\
&{ }^{13} \mathrm{~N} \rightarrow{ }^{13} \mathrm{C}+e^{+}+v_{e}, \\
&{ }^{13} \mathrm{C}+{ }^{1} \mathrm{H} \rightarrow{ }^{14} \mathrm{~N}+\gamma, \\
&{ }^{14} \mathrm{~N}+{ }^{1} \mathrm{H} \rightarrow{ }^{15} \mathrm{O}+\gamma, \\
&{ }^{15} \mathrm{O} \rightarrow{ }^{15} \mathrm{~N}+e^{+}+v_{e}, \\
&{ }^{15} \mathrm{~N}+{ }^{1} \mathrm{H} \rightarrow{ }^{12} \mathrm{C}+{ }^{4} \mathrm{He} .
\end{aligned} \nonumber\]
Write down the overall effect of the carbon cycle (as was done for the proton-proton cycle in \(2 e^{-}+4^{1} \mathrm{H} \rightarrow{ }^{4} \mathrm{He}+2 v_{e}+6 \gamma\)). Note the number of protons (\({ }^{1} \mathrm{H}\)) required and assume that the positrons ( \(e^{+}\)) annihilate electrons to form more \(\gamma\) rays.
Solution
\(2 e^{-}+4^{1} \mathrm{H} \rightarrow{ }^{4} \mathrm{He}+7 \gamma+2 v_{e}\)
151. (a) Find the total energy released in MeV in each carbon cycle (elaborated in the above problem) including the annihilation energy.
(b) How does this compare with the proton-proton cycle output?
152. Verify that the total number of nucleons, total charge, and electron family number are conserved for each of the fusion reactions in the carbon cycle given in the above problem. (List the value of each of the conserved quantities before and after each of the reactions.)
Solution
(a) \(A=12+1=13, Z=6+1=7, \text { efn }=0=0\)
(b) \(A=13=13, Z=7=6+1, \text { efn }=0=-1+1\)
(c) \(A=13+1=14, Z=6+1=7, \text { efn }=0=0\)
(d) \(A=14+1=15, Z=7+1=8, \text { efn }=0=0\)
(e) \(A=15=15, Z=8=7+1, \text { efn }=0=-1+1\)
(f) \(A=15+1=12+4, Z=7+1=6+2, \text { efn }=0=0\)
Integrated Concepts
153. The laser system tested for inertial confinement can produce a 100-kJ pulse only 1.00 ns in duration.
(a) What is the power output of the laser system during the brief pulse?
(b) How many photons are in the pulse, given their wavelength is \(1.06 ~\mu \mathrm{m}\)?
(c) What is the total momentum of all these photons?
(d) How does the total photon momentum compare with that of a single 1.00 MeV deuterium nucleus?
Integrated Concepts
154. Find the amount of energy given to the \({ }^{4} \mathrm{He}\) nucleus and to the \(\gamma\) ray in the reaction \(n+{ }^{3} \mathrm{He} \rightarrow{ }^{4} \mathrm{He}+\gamma\), using the conservation of momentum principle and taking the reactants to be initially at rest. This should confirm the contention that most of the energy goes to the \(\gamma\) ray.
Solution
\(E_{\gamma}=20.6 \mathrm{~MeV}\)
\(E_{ {}^4 \mathrm{He}}=5.68 \times 10^{-2} \mathrm{~MeV}\)
Integrated Concepts
155. (a) What temperature gas would have atoms moving fast enough to bring two \({ }^{3} \mathrm{He}\) nuclei into contact? Note that, because both are moving, the average kinetic energy only needs to be half the electric potential energy of these doubly charged nuclei when just in contact with one another.
(b) Does this high temperature imply practical difficulties for doing this in controlled fusion?
Integrated Concepts
156. (a) Estimate the years that the deuterium fuel in the oceans could supply the energy needs of the world. Assume world energy consumption to be ten times that of the United States which is \(8 \times 10^{19}\) J/y and that the deuterium in the oceans could be converted to energy with an efficiency of 32%. You must estimate or look up the amount of water in the oceans and take the deuterium content to be 0.015% of natural hydrogen to find the mass of deuterium available. Note that approximate energy yield of deuterium is \(3.37 \times 10^{14}\) J/kg.
(b) Comment on how much time this is by any human measure. (It is not an unreasonable result, only an impressive one.)
Solution
(a) \(3 \times 10^{9} y\)
(b) This is approximately half the lifetime of the Earth.
15.9: Fission
157. (a) Calculate the energy released in the neutron-induced fission (similar to the spontaneous fission in Example)
\[n+{ }^{238} \mathrm{U} \rightarrow{ }^{96} \mathrm{Sr}+{ }^{140} \mathrm{Xe}+3 n, \nonumber\]
given \(m\left({ }^{96} \mathrm{Sr}\right)=95.921750 \mathrm{~u}\) and \(m\left({ }^{140} \mathrm{Xe}\right)=139.92164\).
(b) This result is about 6 MeV greater than the result for spontaneous fission. Why? (c) Confirm that the total number of nucleons and total charge are conserved in this reaction.
Solution
(a) 177.1 MeV
(b) Because the gain of an external neutron yields about 6 MeV, which is the average \(BE/A\) for heavy nuclei.
(c) \(A=1+238=96+140+1+1+1, Z=92=38+53, \text { efn }=0=0\)
158. (a) Calculate the energy released in the neutron-induced fission reaction
\[n+{ }^{235} \mathrm{U} \rightarrow{ }^{92} \mathrm{Kr}+{ }^{142} \mathrm{Ba}+2 n, \nonumber\]
given \(m\left({ }^{92} \mathrm{Kr}\right)=91.926269 \mathrm{~u}\) and \(m\left({ }^{142} \mathrm{Ba}\right)=141.916361 \mathrm{~u}\).
(b) Confirm that the total number of nucleons and total charge are conserved in this reaction.
159. (a) Calculate the energy released in the neutron-induced fission reaction
\[n+{ }^{239} \mathrm{Pu} \rightarrow{ }^{96} \mathrm{Sr}+{ }^{140} \mathrm{Ba}+4 n, \nonumber\]
given \(m\left({ }^{96} \mathrm{Sr}\right)=95.921750 \mathrm{~u}\) and \(m\left({ }^{140} \mathrm{Ba}\right)=139.910581 \mathrm{~u}\).
(b) Confirm that the total number of nucleons and total charge are conserved in this reaction.
Solution
(a) 180.6 MeV
(b) \(A=1+239=96+140+1+1+1+1, Z=94=38+56, \text { efn }=0=0\)
160. Breeding plutonium produces energy even before any plutonium is fissioned. (The primary purpose of the four nuclear reactors at Chernobyl was breeding plutonium for weapons. Electrical power was a by-product used by the civilian population.) Calculate the energy produced in each of the reactions listed for plutonium breeding just following Example 15.9.2. The pertinent masses are \(m\left({ }^{239} \mathrm{U}\right)=239.054289 \mathrm{U}\), \(m\left({ }^{239} \mathrm{Np}\right)=239.052932 \mathrm{~u}\), and \(m\left({ }^{239} \mathrm{Pu}\right)=239.052157 \mathrm{~u}\).
Solution
\({ }^{238} \mathrm{U}+n \rightarrow{ }^{239} \mathrm{U}+\gamma\) 4.81 MeV
\({ }^{239} \mathrm{U} \rightarrow{ }^{239} \mathrm{Np}+\beta^{-}+v_{e}\) 0.753 MeV
\({ }^{239} \mathrm{Np} \rightarrow{ }^{239} \mathrm{Pu}+\beta^{-}+v_{e}\) 0.211 MeV
161. The naturally occurring radioactive isotope \({ }^{232} \mathrm{Th}\) does not make good fission fuel, because it has an even number of neutrons; however, it can be bred into a suitable fuel (much as \({ }^{238} \mathrm{U}\) is bred into \({ }^{239} \mathrm{P}\)).
(a) What are \(Z\) and \(N\) for \({ }^{232} \mathrm{Th}\)?
(b) Write the reaction equation for neutron captured by \({ }^{232} \mathrm{Th}\) and identify the nuclide \({ }^{A} X\) produced in \(n+{ }^{232} \mathrm{Th} \rightarrow{ }^{A} X+\gamma\).
(c) The product nucleus \(\beta^{-}\) decays, as does its daughter. Write the decay equations for each, and identify the final nucleus.
(d) Confirm that the final nucleus has an odd number of neutrons, making it a better fission fuel.
(e) Look up the half-life of the final nucleus to see if it lives long enough to be a useful fuel.
162. The electrical power output of a large nuclear reactor facility is 900 MW. It has a 35.0% efficiency in converting nuclear power to electrical.
(a) What is the thermal nuclear power output in megawatts?
(b) How many \({ }^{235} \mathrm{U}\) nuclei fission each second, assuming the average fission produces 200 MeV?
(c) What mass of \({ }^{235} \mathrm{U}\) is fissioned in one year of full-power operation?
Solution
(a) \(2.57 \times 10^{3} \mathrm{~MW}\)
(b) \(8.03 \times 10^{19} \text { fission/s }\)
(c) 991 kg
163. A large power reactor that has been in operation for some months is turned off, but residual activity in the core still produces 150 MW of power. If the average energy per decay of the fission products is 1.00 MeV, what is the core activity in curies?
15.10: Nuclear Weapons
164. Find the mass converted into energy by a 12.0-kT bomb.
Solution
0.56 g
165. What mass is converted into energy by a 1.00-MT bomb?
166. Fusion bombs use neutrons from their fission trigger to create tritium fuel in the reaction \(n+{ }^{6} \mathrm{Li} \rightarrow{ }^{3} \mathrm{H}+{ }^{4} \mathrm{He}\). What is the energy released by this reaction in MeV?
Solution
4.781 MeV
167. It is estimated that the total explosive yield of all the nuclear bombs in existence currently is about 4,000 MT.
(a) Convert this amount of energy to kilowatt-hours, noting that \(1 \mathrm{~kW} \cdot \mathrm{h}=3.60 \times 10^{6} \mathrm{~J}\).
(b) What would the monetary value of this energy be if it could be converted to electricity costing 10 cents per kW·h?
168. A radiation-enhanced nuclear weapon (or neutron bomb) can have a smaller total yield and still produce more prompt radiation than a conventional nuclear bomb. This allows the use of neutron bombs to kill nearby advancing enemy forces with radiation without blowing up your own forces with the blast. For a 0.500-kT radiation-enhanced weapon and a 1.00-kT conventional nuclear bomb:
(a) Compare the blast yields.
(b) Compare the prompt radiation yields.
Solution
(a) Blast yields \(2.1 \times 10^{12} \mathrm{~J}\) to \(8.4 \times 10^{11} \mathrm{~J}\), or 2.5 to 1, conventional to radiation enhanced.
(b) Prompt radiation yields \(6.3 \times 10^{11} \mathrm{~J}\) to \(2.1 \times 10^{11} \mathrm{~J}\), or 3 to 1, radiation enhanced to conventional.
169. (a) How many \({ }^{239} \mathrm{Pu}\) nuclei must fission to produce a 20.0-kT yield, assuming 200 MeV per fission?
(b) What is the mass of this much \({ }^{239} \mathrm{Pu}\)?
170. Assume one-fourth of the yield of a typical 320-kT strategic bomb comes from fission reactions averaging 200 MeV and the remainder from fusion reactions averaging 20 MeV.
(a) Calculate the number of fissions and the approximate mass of uranium and plutonium fissioned, taking the average atomic mass to be 238.
(b) Find the number of fusions and calculate the approximate mass of fusion fuel, assuming an average total atomic mass of the two nuclei in each reaction to be 5.
(c) Considering the masses found, does it seem reasonable that some missiles could carry 10 warheads? Discuss, noting that the nuclear fuel is only a part of the mass of a warhead.
Solution
(a) \(1.1 \times 10^{25} \text { fissions }\) , 4.4 kg
(b) \(3.2 \times 10^{26} \text { fusions }\) , 2.7 kg
(c) The nuclear fuel totals only 6 kg, so it is quite reasonable that some missiles carry 10 overheads. The mass of the fuel would only be 60 kg and therefore the mass of the 10 warheads, weighing about 10 times the nuclear fuel, would be only 1500 lbs. If the fuel for the missiles weighs 5 times the total weight of the warheads, the missile would weigh about 9000 lbs or 4.5 tons. This is not an unreasonable weight for a missile.
171. This problem gives some idea of the magnitude of the energy yield of a small tactical bomb. Assume that half the energy of a 1.00-kT nuclear depth charge set off under an aircraft carrier goes into lifting it out of the water—that is, into gravitational potential energy. How high is the carrier lifted if its mass is 90,000 tons?
172. It is estimated that weapons tests in the atmosphere have deposited approximately 9 MCi of \({ }^{90} \mathrm{Sr}\) on the surface of the earth. Find the mass of this amount of \({ }^{90} \mathrm{Sr}\).
Solution
\(7 \times 10^{4} \mathrm{~g}\)
173. A 1.00-MT bomb exploded a few kilometers above the ground deposits 25.0% of its energy into radiant heat.
(a) Find the calories per \(\mathrm{cm}^{2}\) at a distance of 10.0 km by assuming a uniform distribution over a spherical surface of that radius.
(b) If this heat falls on a person’s body, what temperature increase does it cause in the affected tissue, assuming it is absorbed in a layer 1.00-cm deep?
Integrated Concepts
174. One scheme to put nuclear weapons to nonmilitary use is to explode them underground in a geologically stable region and extract the geothermal energy for electricity production. There was a total yield of about 4,000 MT in the combined arsenals in 2006. If 1.00 MT per day could be converted to electricity with an efficiency of 10.0%:
(a) What would the average electrical power output be?
(b) How many years would the arsenal last at this rate?
Solution
(a) \(4.86 \times 10^{9} \mathrm{~W}\)
(b) 11.0 y
15.11: The Four Basic Forces
175. (a) Find the ratio of the strengths of the weak and electromagnetic forces under ordinary circumstances.
(b) What does that ratio become under circumstances in which the forces are unified?
Solution
(a) 10−11 to 1, weak to EM
(b) 1 to 1
176. The ratio of the strong to the weak force and the ratio of the strong force to the electromagnetic force become 1 under circumstances where they are unified. What are the ratios of the strong force to those two forces under normal circumstances?
15.12: Particles, Patterns, and Conservation Laws
177. The\(\pi^{0}\) is its own antiparticle and decays in the following manner: \(\pi^{0} \rightarrow \gamma+\gamma\). What is the energy of each \(\gamma\) ray if the\(\pi^{0}\) is at rest when it decays?
Solution
67.5 MeV
178. The primary decay mode for the negative pion is \(\pi^{-} \rightarrow \mu^{-}+\bar{\nu}_{\mu}\). What is the energy release in MeV in this decay?
179. The mass of a theoretical particle that may be associated with the unification of the electroweak and strong forces is \(10^{14} \mathrm{~GeV} / c^{2}\).
(a) How many proton masses is this?
(b) How many electron masses is this? (This indicates how extremely relativistic the accelerator would have to be in order to make the particle, and how large the relativistic quantity \(\gamma\) would have to be.)
Solution
(a) 1 × 1014
(b) 2 × 1017
180. The decay mode of the negative muon is \(\mu^{-} \rightarrow e^{-}+\bar{\nu}_{e}+\nu_{\mu}\).
(a) Find the energy released in MeV.
(b) Verify that charge and lepton family numbers are conserved.
181. The decay mode of the positive tau is \(\tau^{+} \rightarrow \mu^{+}+\nu_{\mu}+\bar{\nu}_{\tau}\).
(a) What energy is released?
(b) Verify that charge and lepton family numbers are conserved.
(c) The \(\tau^{+}\) is the antiparticle of the \(\tau^{-}\).Verify that all the decay products of the \(\tau^{+}\) are the antiparticles of those in the decay of the \(\tau^{-}\) given in the text.
Solution
(a) 1671 MeV
(b) \(Q=1, Q^{\prime}=1+0+0=1 . L_{\tau}=-1 ; L^{\prime} \tau=-1 ; L \mu=0 ; L^{\prime} \mu=-1+1=0\)
(c) \(\begin{aligned}
&\tau^{-} \rightarrow \mu^{-}+v_{\mu}+\bar{v}_{\tau} \\
&\Rightarrow \mu^{-} \text {antiparticle of } \mu^{+} ; v_{\mu} \text { of } \bar{v}_{\mu} ; \bar{v}_{\tau} \text { of } v_{\tau}
\end{aligned}\)
182. The principal decay mode of the sigma zero is \(\Sigma^{0} \rightarrow \Lambda^{0}+\gamma\).
(a) What energy is released?
(b) Considering the quark structure of the two baryons, does it appear that the \(\Sigma^{0}\) is an excited state of the \(\Lambda^{0}\)?
(c) Verify that strangeness, charge, and baryon number are conserved in the decay.
(d) Considering the preceding and the short lifetime, can the weak force be responsible? State why or why not.
183. (a) What is the uncertainty in the energy released in the decay of a\(\pi^{0}\) due to its short lifetime?
(b) What fraction of the decay energy is this, noting that the decay mode is \(\pi^{0} \rightarrow \gamma+\gamma\) (so that all the\(\pi^{0}\) mass is destroyed)?
Solution
(a) 3.9 eV
(b) 2.9 × 10−8
184. (a) What is the uncertainty in the energy released in the decay of a \(\tau^{-}\) due to its short lifetime?
(b) Is the uncertainty in this energy greater than or less than the uncertainty in the mass of the tau neutrino? Discuss the source of the uncertainty.
15.13: GUTs- The Unification of Forces
Integrated Concepts
185. The intensity of cosmic ray radiation decreases rapidly with increasing energy, but there are occasionally extremely energetic cosmic rays that create a shower of radiation from all the particles they create by striking a nucleus in the atmosphere as seen in the figure given below. Suppose a cosmic ray particle having an energy of \(10^{10} \mathrm{~GeV}\)converts its energy into particles with masses averaging \(200 \mathrm{~MeV} / c^{2}\).
(a) How many particles are created?
(b) If the particles rain down on a \(1.00-\mathrm{km}^{2}\) area, how many particles are there per square meter?
Solution
(a) 5 × 1010
(b) 5 × 104 particles/m2
Integrated Concepts
186. Assuming conservation of momentum, what is the energy of each \(\gamma\) ray produced in the decay of a neutral at rest pion, in the reaction \(\pi^{0} \rightarrow \gamma+\gamma\)?
Integrated Concepts
187. What is the wavelength of a 50-GeV electron, which is produced at SLAC? This provides an idea of the limit to the detail it can probe.
Solution
2.5 × 10−17 m
Integrated Concepts
188. (a) Calculate the relativistic quantity \(\gamma=\frac{1}{\sqrt{1-v^{2} / c^{2}}}\) for 1.00-TeV protons produced at Fermilab.
(b) If such a proton created a \(\pi^{+}\) having the same speed, how long would its life be in the laboratory? (c) How far could it travel in this time?
Integrated Concepts
189. The primary decay mode for the negative pion is \(\pi^{-} \rightarrow \mu^{-}+\bar{\nu}_{\mu}\).
(a) What is the energy release in MeV in this decay?
(b) Using conservation of momentum, how much energy does each of the decay products receive, given the \(\pi^{-}\) is at rest when it decays? You may assume the muon antineutrino is massless and has momentum \(p=E / c\), just like a photon.
Solution
(a) 33.9 MeV
(b) Muon antineutrino 29.8 MeV, muon 4.1 MeV (kinetic energy)
Integrated Concepts
190. Plans for an accelerator that produces a secondary beam of K-mesons to scatter from nuclei, for the purpose of studying the strong force, call for them to have a kinetic energy of 500 MeV.
(a) What would the relativistic quantity \(\gamma=\frac{1}{\sqrt{1-v^{2} / c^{2}}}\) be for these particles?
(b) How long would their average lifetime be in the laboratory?
(c) How far could they travel in this time?
Integrated Concepts
191. Suppose you are designing a proton decay experiment and you can detect 50 percent of the proton decays in a tank of water.
(a) How many kilograms of water would you need to see one decay per month, assuming a lifetime of \(10^{31} \mathrm{~y}\)?
(b) How many cubic meters of water is this?
(c) If the actual lifetime is \(10^{33} \mathrm{~y}\), how long would you have to wait on an average to see a single proton decay?
Solution
(a) 7.2 × 105 kg
(b) 7.2 × 102 m3
(c) 100 months
Integrated Concepts
192. In supernovas, neutrinos are produced in huge amounts. They were detected from the 1987A supernova in the Magellanic Cloud, which is about 120,000 light years away from the Earth (relatively close to our Milky Way galaxy). If neutrinos have a mass, they cannot travel at the speed of light, but if their mass is small, they can get close.
(a) Suppose a neutrino with a \(7-\mathrm{eV} / c^{2}\) mass has a kinetic energy of 700 keV. Find the relativistic quantity \(\gamma=\frac{1}{\sqrt{1-v^{2} / c^{2}}}\) for it.
(b) If the neutrino leaves the 1987A supernova at the same time as a photon and both travel to Earth, how much sooner does the photon arrive? This is not a large time difference, given that it is impossible to know which neutrino left with which photon and the poor efficiency of the neutrino detectors. Thus, the fact that neutrinos were observed within hours of the brightening of the supernova only places an upper limit on the neutrino’s mass. (Hint: You may need to use a series expansion to find v for the neutrino, since its \(\gamma\) is so large.)
Construct Your Own Problem
193. Consider an ultrahigh-energy cosmic ray entering the Earth’s atmosphere (some have energies approaching a joule). Construct a problem in which you calculate the energy of the particle based on the number of particles in an observed cosmic ray shower. Among the things to consider are the average mass of the shower particles, the average number per square meter, and the extent (number of square meters covered) of the shower. Express the energy in eV and joules.
Construct Your Own Problem
194. Consider a detector needed to observe the proposed, but extremely rare, decay of an electron. Construct a problem in which you calculate the amount of matter needed in the detector to be able to observe the decay, assuming that it has a signature that is clearly identifiable. Among the things to consider are the estimated half life (long for rare events), and the number of decays per unit time that you wish to observe, as well as the number of electrons in the detector substance.