5.8: Kirchhoff’s Rules
- Page ID
- 6016
We can even adapt Kirchhoff’s rules to deal with capacitors. Thus, connect a 24 \(\text{V}\) battery across the circuit of Figure \(V.8\) – see Figure \(V.9\)
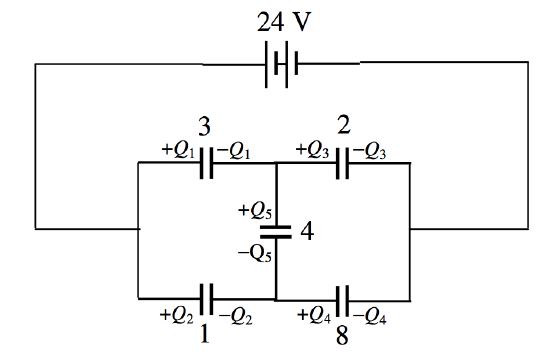
\(\text{FIGURE V.9}\)
Calculate the charge held in each capacitor. We can proceed in a manner very similar to how we did it in Chapter 4, applying the capacitance equivalent of Kirchhoff’s second rule to three closed circuits, and then making up the five necessary equations by applying “Kirchhoff’s first rule” to two points. Thus:
\[24-\frac{Q_2}{3}-\frac{Q_3}{2}=0,\label{5.8.1}\]
\[24-Q_2-\frac{Q_4}{8},\label{5.8.2}\]
\[\frac{Q_1}{3}-Q_2+\frac{Q_5}{4}=0,\]
\[Q_1=Q_3+Q_5,\]
\[Q_4=Q_2+Q_5,\]
I make the solutions
\[Q_1=+41.35\mu \text{C},\,Q_2=+19.01\mu \text{C},\,Q_3=+20.44\mu \text{C},\,Q_4 = +39.92 \mu \text{C},\,Q_5 =20.91 \mu \text{C}.\]


