10.12: Growth of Current in a Circuit Containing Inductance
- Page ID
- 7899
It will have occurred to you that if the growth of current in a coil results in a back EMF which opposes the increase of current, current cannot change instantaneously in a circuit that contains inductance. This is correct. (Recall also that the potential difference in a circuit cannot change instantaneously in a circuit containing capacitance. Come to think of it, it is hardly possible for the capacitance or inductance of any circuit to be exactly zero; any real circuit must have some capacitance and inductance, even if very small.)
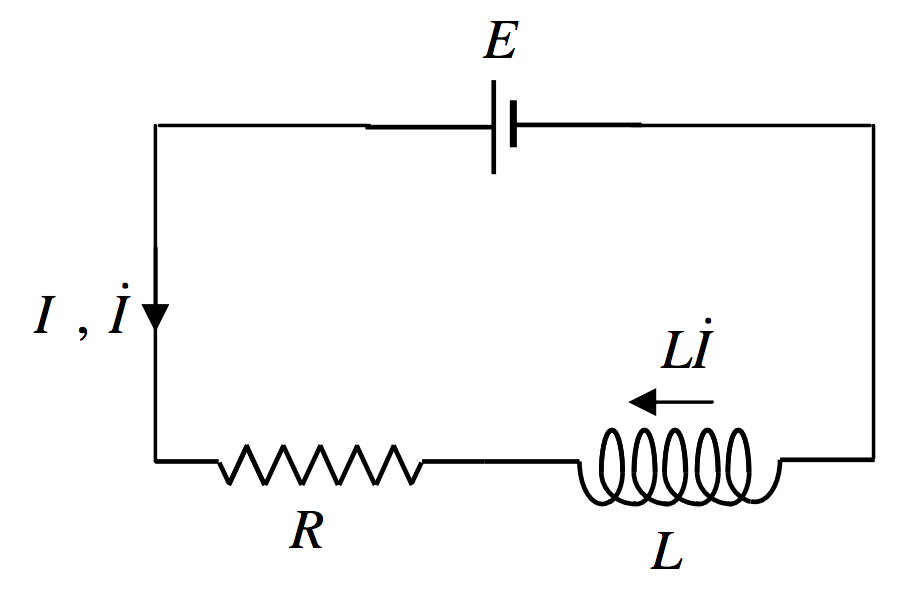
Consider the circuit of Figure X.9. A battery of EMF \(E\) is in series with a resistance and an inductance. (A coil or solenoid or any inductor in general will have both inductance and resistance, so the \(R\) and the \(L\) in the Figure may belong to one single item.) We have to be very careful about signs in what follows.
\(\text{FIGURE X.9}\)
When the circuit is closed (by a switch, for example) a current flows in the direction shown. by an arrow, which also indicates the direction of the increase of current. An EMF \(L\dot I\) is induced in the opposite direction to \(\dot I\). Thus, Ohm's law, or, if your prefer, Kirchhoff's second rule, applied to the circuit (watch the signs carefully) is
\[E=IR -L \dot I=0.\label{10.12.1}\]
Hence:
\[\label{10.12.2}\int_0^I \frac{dI}{\frac{E}{R}-I}=\frac{R}{L}\,dt.\]
Warning: Some people find an almost irresistible urge to write this as \(\int_0^I \frac{dI}{I-\frac{E}{R}}=-\frac{R}{L}\,dt\).
Don't!
You can anticipate that the left hand side is going to be a logarithm, so make sure that the denominator is positive. You may recall a similar warning when we were charging and discharging a capacitor through a resistance.
Integration of Equation \ref{10.12.2} results in the following equation for the growth of the current with time:
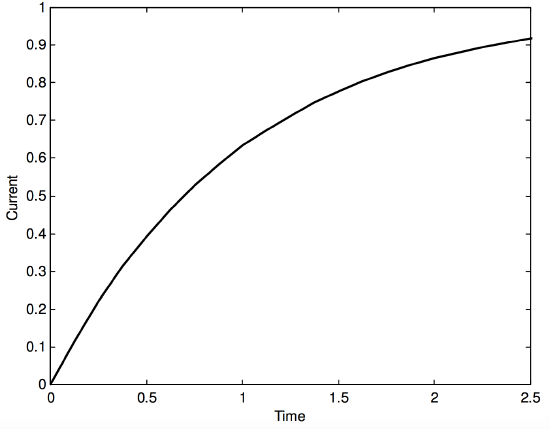
\[I=\frac{E}{R}\left (1-e^{-(R/L)t}\right ) .\label{10.12.3}\]
Thus the current asymptotically approaches its ultimate value of \(E/R\), reaching 63% (i.e. \(1-e^{-1}\) ) of its ultimate value in a time \(L/R\). In Figure X.10, the current is shown in units of \(E/R\), and the time in units of \(L/R\). You should check that \(L/R\), which is called the time constant of the circuit, has the dimensions of time.
\(\text{FIGURE X.10}\)
Here is a problem that will give practice in sending a current through an inductor, applying Kirchhoff’s rules, and solving differential equations. There is a similar problem involving a capacitor, in Chapter 5, Section 5.19.
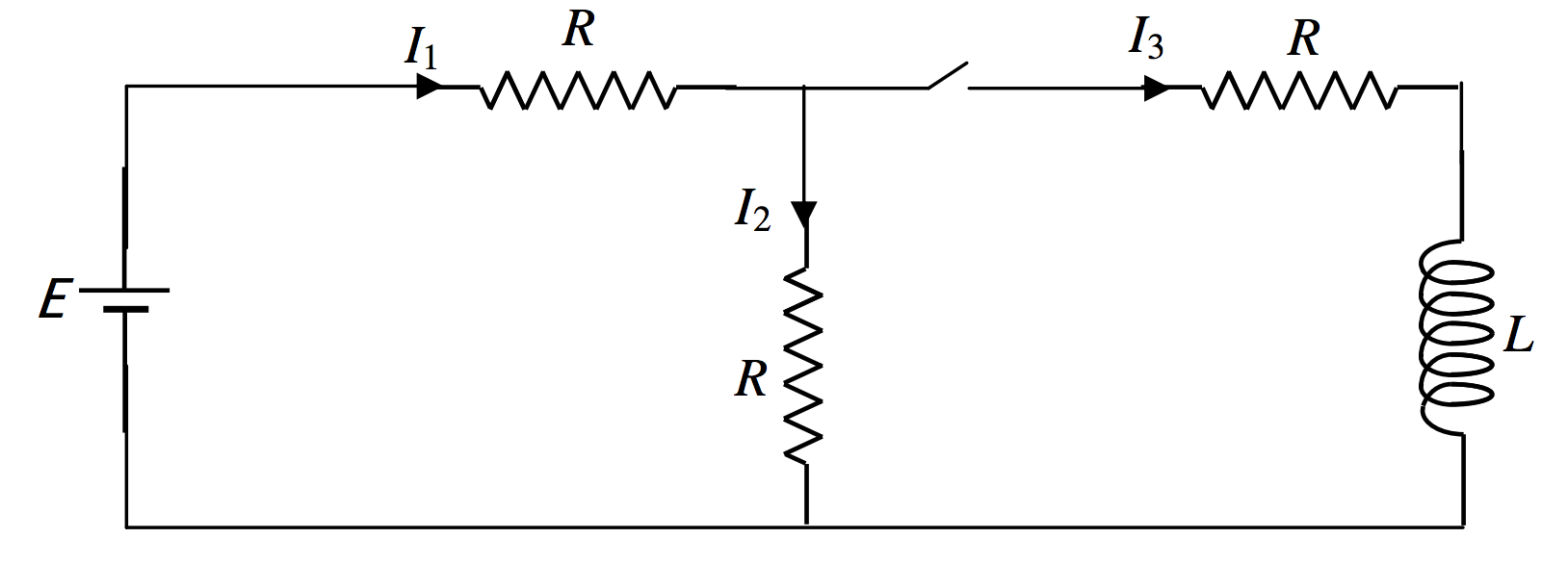
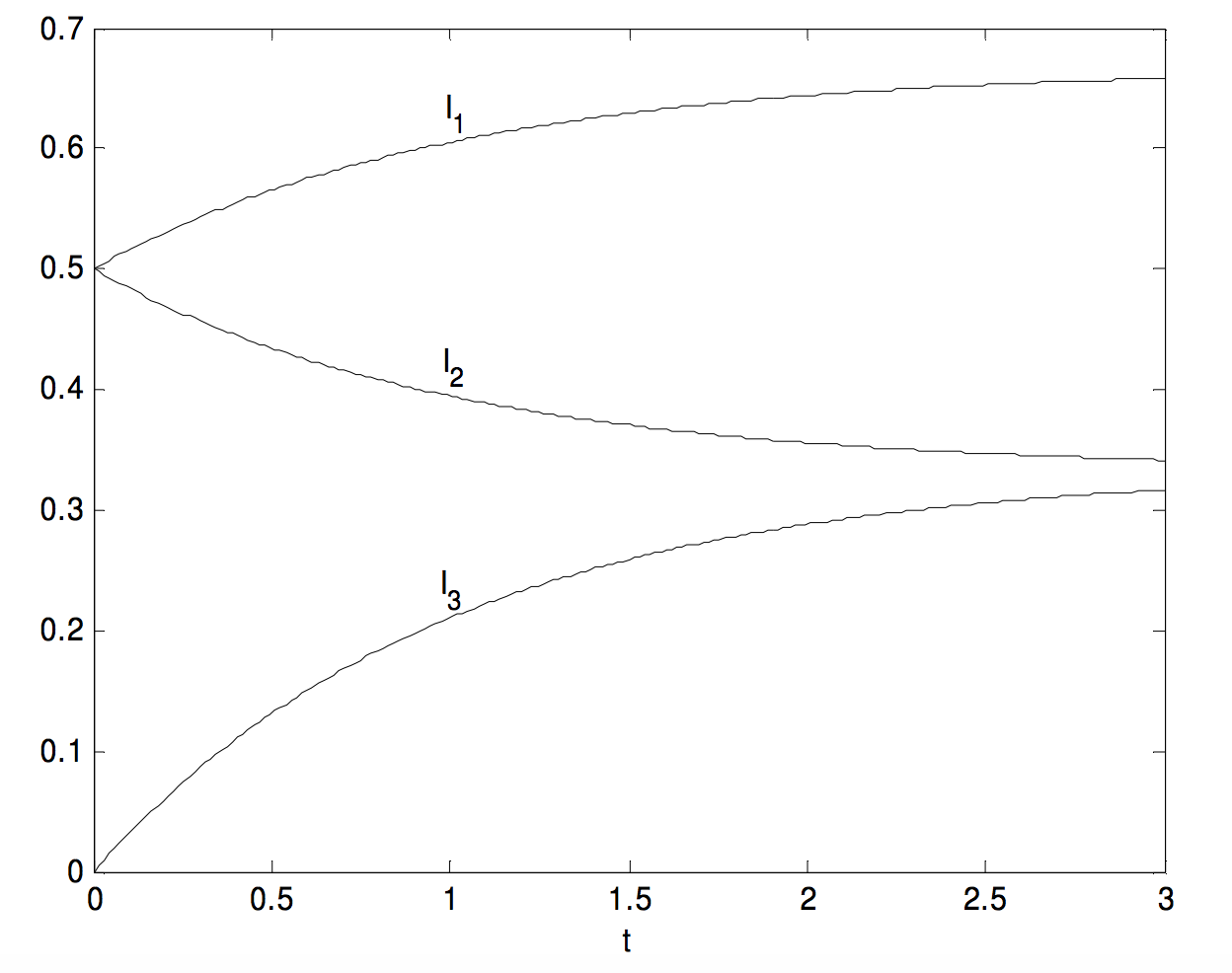
In the above circuit, while the switch is open, \(I_1 = I_2 = E/(2 R)\text{ and }I_3 = 0\). Long after the switch is closed and steady currents have been reached, \(I_1\) will be \( 2E /(3R)\), and \(I_2 \text{ and }I_3\) will each be \(E /(3R)\). But we want to investigate what happens in the brief moment while the current is changing.
We apply Kirchhoff’s rules:
\[\label{10.12.4}E=I_1R+I_2R \]
\[\label{10.12.5}I_3R+L\dot I_3 -I_2R=0\]
\[\label{10.12.6}I_1=I_2+I_3,\]
[Getting the sign of \(L\dot I_3\) right in Equation \ref{10.12.5} is important. Think of the inductor as a battery of EMF \(L\dot I_3\) oriented like this: 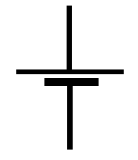 .]
.]
Eliminate \(I_1 \text{ and }I_2\) to get a single equation in \(I_3\).
\[\label{10.12.7}\frac{dI_3}{dt}+\frac{3R}{2L}I_3 =\frac{E}{2L}.\]
This is of the form \(\frac{dy}{dx}+ay=b\), and those experienced with differential equations will have no difficulty in arriving at the solution
\[\label{10.12.8}I_3 = \frac{E}{3R}+Ae^{\frac{3Rt}{2L}}.\]
With the initial condition that \(I_3 = 0 \text{ when }t = 0\), this becomes
\[\label{10.12.9}I_3=\frac{E}{3R}\left ( 1-e^{-\frac{3Rt}{2L}}\right ) \]
The other currents are found from Kirchhoff’s rules (equations \ref{10.12.4}-6). I make them:
\[\label{10.12.10}I_2 = \frac{E}{3R}\left ( 1+\frac{1}{2}e^{-\frac{3Rt}{2L}}\right ) \]
\[\label{10.12.11}I_1 = \frac{E}{3R}\left ( 2-\frac{1}{2}e^{-\frac{3Rt}{2L}}\right )\]
Thus \(I_1\) goes from initially \(\frac{E}{2R}\text{ to finally }\frac{2E}{3R}\).
\(I_2\) goes from initially \(\frac{E}{2R}\text{ to finally }\frac{E}{3R}\).
\(I_3\) goes from initially zero to finally \(\frac{E}{3R}\).
Here are graphs of the currents (in units of \(E/R\)) as a function of time (in units of \(2L /(3R)\)).