10.15: Charging a Capacitor through and Inductance and a Resistance
- Page ID
- 7906
In Section 5.19 we connected a battery to a capacitance and a resistance in series to see how the current in the circuit and the charge in the capacitor varied with time; In this chapter, Section 10.12, we connected a battery to an inductance and a resistance in series to see how the current increased with time. We have not yet connected a battery to \(R\), \(C\), \(L\) in series. We are about to do this. We also recall, from Section 5.19, when we connect a battery to \(C\) and \(R\) in series, the current apparently increases instantaneously from zero to \(E/R\) as soon as we closed the switch. We pointed out that any real circuit (which is necessarily a loop) must have some inductance, however small, and consequently the current takes a finite time, however small, to reach its maximum value after the switch is closed.
The differential equation that shows how the EMF of the battery is equal to the sum of the potential differences across the three elements is
\[\label{10.15.1}E=IR+Q/C+L\dot I \]
If we write \(L=\dot Q\text{ and }\dot I =\ddot Q\) we arrive at the differential equation for the charge in the capacitor:
\[\label{10.15.2}LC\ddot Q +RC\dot Q +Q=EC\]
The general solutions to this are the same as for Equation 10.14.2 except for the addition of the particular integral, which devotees of differential equations will recognize as simply \(EC\). The general solutions for the current I can be found by differentiating the solutions for \(Q\) with respect to time.
Thus the general solutions are
If the resistance is smaller than \(2\sqrt{\frac{L}{C}}\) the charge in the capacitor and the current in the circuit will vary with time as
\[\label{10.15.3}Q=Le^{-\gamma T}\sin (\omega^\prime t+\alpha)+EC.\]
\[\label{10.15.4}I=Ke^{-\gamma t}[\omega ^\prime +\alpha )-\gamma \sin (\omega ^\prime t +\alpha )].\]
The definitions of the constants \(\gamma \text{ and }\omega ^\prime\) were given by equations 10.14.4.
If the resistance is larger than \(2\sqrt{\frac{L}{C}}\) the charge in the capacitor and the current in the circuit will vary with time as
\[\label{10.15.5}Q=Ae^{-\lambda_1t}+Be^{-\lambda_2t}+EC.\]
\[\label{10.15.6}I=-(\lambda_1Ae^{-\lambda_1t}+\lambda_2Be^{-\lambda_2t}).\]
The definitions of the constants \(\lambda_1\text{ and }\lambda_2\) were given by equations 10.14.7.
If the resistance is equal to \(2\sqrt{\frac{L}{C}}\) the charge in the capacitor and the current in the circuit will vary with time as
\[\label{10.15.7}Q=Ke^{-\frac{Rt}{2L}}(1+at)+EC.\]
\[\label{10.15.8}I=Ke^{-\frac{Rt}{2L}}\left [ a-\frac{R}{2L}(1-at)\right ] .\]
The constants of integration can be found from the initial conditions. At \(t = 0,\, Q\), the charge in the capacitor, is zero. (This is different from the example in Section 10.14, where the initial charge was \(Q_0\). Also at \(t = 0\), the current \(I = 0\). Indeed this is one of the motivations for doing this investigation - remember our difficulty in Section 5.19. The results of applying the initial conditions are:
If the resistance is larger than \(2\sqrt{\frac{L}{C}}\) the constants of integration are given by
\[\label{10.15.10}\tan \alpha = \frac{\omega^\prime}{\gamma}\]
and
\[\label{10.15.11}K=-\frac{EC}{\sin \alpha}\]
These could in principle be inserted into equations \ref{10.15.3} and \ref{10.15.4}. For computational purposes it is easier to leave the equations as they are.
If the resistance is larger than \(2\sqrt{\frac{L}{C}}\) the charge in the capacitor and the current in the circuit will vary with time as
\[\label{10.15.12}Q=EC\left [ 1-\left ( \frac{\lambda_2 e^{-\lambda_1 t}-\lambda_1e^{-\lambda_2t}}{\lambda_2 -\lambda_1}\right ) \right ]\]
\[\label{10.15.13}I=EC\left ( \frac{\lambda_1 \lambda_2}{\lambda_2 -\lambda_1}\right ) \left ( e^{-\lambda_1t}-e^{-\lambda_2t}\right ).\]
If the resistance is equal to \(2\sqrt{\frac{L}{C}}\) the charge in the capacitor and the current in the circuit will vary with time as
\[\label{10.15.14}Q=EC\left [ 1-e^{-Rt/(2L)}\left ( 1+\frac{Rt}{2L}\right ) \right ]\]
\[\label{10.15.15}I=\frac{ECR^2}{4L^2}te^{-Rt/(2L)}.\]
It will be noted, in all three cases, that the complementary function of the solution to the differential equation is a transient which eventually disappears, while the particular integral represents the final steady state solution. Readers may have noticed that, when a fuse blows, it often blows just when you switch on; it is the transient surge that strikes the fatal blow.
The situation that initially interested us in this problem was the case when the inductance in the circuit was very small - that is, when the resistance is larger than \(2\sqrt{\frac{L}{C}}\). We were concerned that, when the inductance was actually zero, the current apparently immediately rose to \(EC\) as soon as the switch was closed. So let us look at Equation \ref{10.15.13}. If we multiply both sides by \(CR\) it can then be written in dimensionless form as
\[\label{10.15.16}\frac{I}{E/R}=\left ( \frac{l_1 l_2}{l_2-l_1}\right ) \left (e^{-l_1\tau}-e^{-l_2\tau}\right ),\]
where
\[\label{10.15.17}\tau=t/(CR) \quad \text{and}\quad l_i = CR\lambda_i .\]
In other words we are expressing time in units of \(CR\).
It can be observed, by differentiation of Equation \ref{10.15.16}, that the current will reach a maximum value (which is less than \(E/R\)) at time given by
\[\label{10.15.18}\tau = \frac{\ln (l_2/l_1)}{l_2-l_1}=\frac{\ln (\lambda_2/\lambda_1)}{\lambda_2-\lambda_1}.\]
The two \(\lambda\) constants, first defined in equations 10.14.7, can be written in the form
\[\label{10.15.19}\lambda_1 =\frac{R}{2L}\left [ 1-\sqrt{1-\frac{4(L/R)}{RC}}\right ] ,\, \lambda_2 = \frac{R}{2L}\left [ 1+\sqrt{1-\frac{4(L/R)}{RC}}\right ] \]
I introduce the dimensionless ratio
\[\label{10.15.20}x=\frac{L/R}{CR},\]
so that
\[\label{10.15.21}l_1=\frac{1-\sqrt{1-4x}}{2x},\quad l_2 =\frac{1+\sqrt{1-4x}}{2x}\]
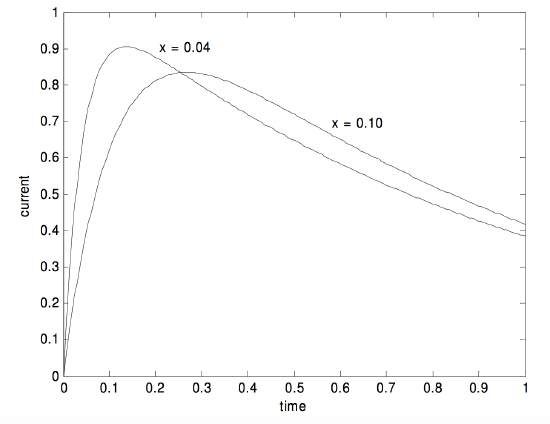
In the table and graph below I show how the current \(I\) changes with time (Equation \ref{10.15.13}, or, in dimensionless form, \ref{10.15.16}) for \(x=\frac{1}{10}\) and for \(x=\frac{1}{25}\). The current is given in units of \(E/R\), and the time is in units of \(RC\). Only if the inductance of the circuit is exactly zero (which cannot possibly be obtained in any real closed circuit) will the current jump immediately from 0 to \(E/R\) at the instant when the switch is closed.
\[\nonumber \begin{matrix} x & l_1 & l_2 & \frac{l_1l_2}{l_2-l_1} & \tau_{max} & \frac{I_{max}}{E/R} \\ \nonumber \\ \nonumber 0.10 & 1.12702 & 8.87298 & 1.29099 & 0.26639 & 0.83473 \\ \nonumber 0.04 & 1.04356 & 23.95644 & 1.09109 & 0.13676 & 0.90476 \\ \end{matrix}\]