14.12: Another Example
- Page ID
- 5847
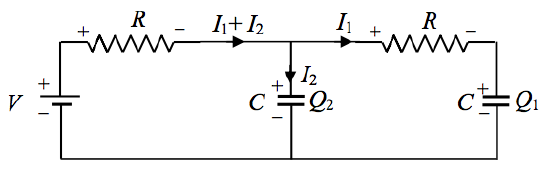
\(\text{FIGURE XIV.1}\)
The circuit in figure \(\text{XIV.1}\) contains two equal resistances, two equal capacitances, and a battery. The battery is connected at time \(t=0\). Find the charges held by the capacitors after time \(t\).
Apply Kirchhoff’s second rule to each half:
\[(\dot Q_1 + \dot Q_2)RC + Q_2 = CV, \tag{14.12.1}\]
and \[\dot Q_1 RC + Q_1 - Q_2 = 0.\tag{14.12.2}\]
Eliminate \(Q_2\):
\[R^2C^2\ddot Q_1 + 3 RC Q_1 + Q_1 = CV. \tag{14.12.3}\]
Transform, with \(Q_1\) and \(\dot Q_1\) initially zero:
\[(R^2C^2s^2 + 3RCs + 1) \bar{Q_1} = \frac{CV}{s}.\tag{14.12.4}\]
I.e. \[R^2C\bar{Q_1} = \frac{1}{s(s^2 + 3as + a^2)} \cdot V , \tag{14.12.5}\]
where \[a=1/(RC). \tag{14.12.6}\]
That is \[R^2C \bar{Q_1}= \frac{1}{s(s+2.618a)(s+0.382a)}V. \tag{14.12.7}\]
Partial fractions: \[R^2C\bar{Q_1} = \left[\frac{1}{s} + \frac{0.1708}{s+2.618a} - \frac{1.1708}{s+0.382a} \right] \frac{V}{a^2}. \tag{14.12.8}\]
That is, \[\bar{Q_1} = \left[ \frac{1}{s} + \frac{0.1708}{s+2.618a} - \frac{1.1708}{s+0.382a} \right]CV. \tag{14.12.9}\]
Inverse transform: \[Q_1 = \left[ 1 + 0.1708e^{-2.618t/(RC)} - 1.1708e^{-0.382t/(RC)} \right]. \tag{14.12.10}\]
The current can be found by differentiation.
I leave it to the reader to eliminate \(Q_1\) from equations 14.12.1 and 2 and hence to show that
\[Q_2 = \left[1 - 0.2764 e^{-2.618 t/(RC)} - 0.7236 e^{-0.382 t/(RC)} \right]. \tag{14.12.11}\]