16.6: Dimensions
( \newcommand{\kernel}{\mathrm{null}\,}\)
A book says that the equivalent width W, in wavelength units, of a spectrum line, is related to the number of atoms per unit area in the line of sight, N, by
W= \frac{\pi e^2 N \lambda^2}{mc^2}.
Is this formula all right in any system of units? Can I use SI units on the right hand side, and get the answer in metres? Or must I use a particular set of units in order to get the right answer? And if so, which units?
A book says that the rate at which energy is radiated, P, from an accelerating charge is
P = \frac{2e^2\ddot x^2}{c^3}.
Is this correct? Is c the speed of light, or is it merely a conversion factor between different units? Or is one of the cs a conversion factor, and the other two are the speed of light?
It is possible to find the answer to such bewildering questions, if we do a bit of dimensional analysis. So, before trying to answer these specific questions (which I shall do later as examples) I am going to present a table of dimensions. I already gave a table of dimensions of electrical quantities in Chapter 11, in terms of \text{M, L, T} and \text{Q}, but that table won’t be particularly helpful in the present context.
I pointed out in Section 16.1 of the present chapter that Coulomb’s law is often written in the form
F= \frac{Q_1Q_2}{r^2}.
Consequently the dimensions of Q are held to be [Q]= \text{M}^{1/2}\text{L}^{3/2}\text{T}^{-1}. But we know that a permittivity is missing from the denominator of equation 16.6.3, because the writer intends his formula to be restricted to a particular set of units such that k or 4 \pi \epsilon_0 = 1. In order to detect whether a permittivity has been omitted from an equation, we need a table in which the dimensions of electrical quantities are given not in terms of \text{M, L, T} and \text{Q} as in Chapter 11, but in terms of \text{M, L, T} and \epsilon, and this is what I am just about to do. However, often it is the permeability that has been omitted from an equation, and, in order to detect whether this is so, I am also supplying a table in which the dimensions of electrical quantities are given in terms of \text{M, L, T} and \mu.
If, from dimensional analysis, you find that an expression is dimensionally wrong by a power of the permittivity, insert 4\pi \epsilon_0 in the appropriate part of the equation. If you find that an expression is dimensionally wrong by a power of the permeability, insert \mu_0 / (4 \pi) in the appropriate part of the equation. If you find that the equation is wrong by \text{LT}^{-1}, insert or delete c as appropriate. Your equation will then balance dimensionally and will be ready for use in any coherent system of units, including SI. This procedure will probably work in most cases, but I cannot guarantee that it will work in all cases, because it cannot deal with those (frequent!) cases in which the formula given is plain wrong, whatever units are used!
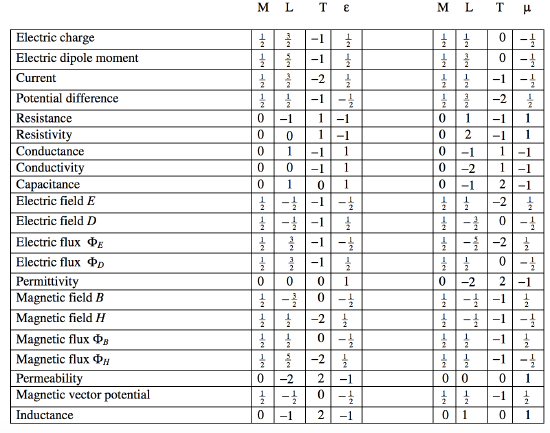
Now let’s look at the equation for equivalent width of a spectrum line:
\nonumber W= \frac{\pi e^2 N \lambda^2}{mc^2}. \tag{16.6.1}
Here [W] = \text{L} and [N] = \text{L}^{-2}. By making use of the table we find that the dimensions of the right hand side are \text{L} \epsilon. There is therefore a 4 \pi \epsilon_0 missing from the denominator, and the equation should be
W = \frac{\pi e^2 N \lambda^2}{4 \pi \epsilon_0 m c^2}.
How about the rate at which energy is radiated from an accelerating charge?
\nonumber P = \frac{2e^2\ddot x^2}{c^3}. \tag{16.6.2}
Power has dimensions \text{ML}^2 \text{T}^{−3}, whereas the dimensions of the right hand side are \text{ML}^2 \text{T}^{−3} \epsilon, so again there is a 4 \pi \epsilon_0 missing from the denominator and the formula should be
P = \frac{2 e^2 \ddot x^2}{4 \pi \epsilon_0 c^3}.
It is often the case that there is a 4 \pi \epsilon_0 missing from the denominator is formulas that have an e^2 upstairs.
“Electromagnetic” formulas often give more difficulty. For example, one book says that the energy per unit volume in a magnetic field in vacuo is \frac{B^2}{8 \pi}, while another says that is it is \frac{H^2}{8 \pi}. Which is it (if indeed it is either)? Energy per unit volume has dimensions \text{ML}^{−1} \text{T}^{−2}. The dimensions of B^2 are \text{ML}^{−1} \text{T}^{−2} \mu. The equation given is therefore wrong dimensionally by permeability, and the equation should be divided by \mu_0 / (4 \pi) to give B^2/(2\mu_0), which is correct. On the other hand, the dimensions of H^2 are \text{ML}^{−1} \text{T}^{−2} \mu^{−1}, so perhaps we should multiply by \mu_0/(4 \pi)? But this does not give a correct answer, and it exemplifies some of the many difficulties that are caused by writing formulas that do not balance dimensionally and are intended to be used only with a particular set of units. The situation is particularly difficult with respect to magnetic moment, a subject to which I shall devote the next chapter.


