5.20: Real Capacitors
- Page ID
- 6031
Real capacitors can vary from huge metal plates suspended in oil to the tiny cylindrical components seen inside a radio. A great deal of information about them is available on the Web and from manufacturers’ catalogs, and I only make the briefest remarks here.
A typical inexpensive capacitor seen inside a radio is nothing much more than two strips of metal foil separated by a strip of plastic or even paper, rolled up into a cylinder much like a Swiss roll. Thus the separation of the “plates” is small, and the area of the plates is as much as can be conveniently rolled into a tiny radio component.
In most applications it doesn’t matter which way round the capacitor is connected. However, with some capacitors it is intended that the outermost of the two metal strips be grounded (“earthed” in UK terminology), and the inner one is shielded by the outer one from stray electric fields. In that case the symbol used to represent the capacitor is
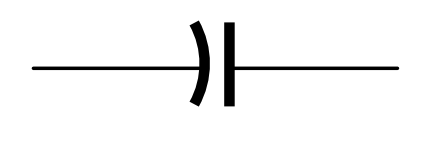
The curved line is the outer strip, and is the one that is intended to be grounded. It should be noted, however, that not everyone appears to be aware of this convention or adheres to it, and some people will use this symbol to denote any capacitor. Therefore care must be taken in reading the literature to be sure that you know what the writer intended, and, if you are describing a circuit yourself, you must make very clear the intended meaning of your symbols.
There is a type of capacitor known as an electrolytic capacitor. The two “plates” are strips of aluminium foil separated by a conducting paste, or electrolyte. One of the foils is covered by an extremely thin layer of aluminium oxide, which has been electrolytically deposited, and it is this layer than forms the dielectric medium, not the paste that separates the two foils. Because of the extreme thinness of the oxide layer, the capacitance is relatively high, although it may not be possible to control the actual thickness with great precision and consequently the actual value of the capacitance may not be known with great precision. It is very important that an electrolytic capacitor be corrected the right way round in a circuit, otherwise electrolysis will start to remove the oxide layer from one foil and deposit it on the other, thus greatly changing the capacitance. Also, when this happens, a current may pass through the electrolyte and heat it up so much that the capacitor may burst open with consequent danger to the eyes. The symbol used to indicate an electrolytic capacitor is:
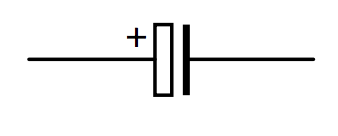
The side indicated with the plus sign (which is often omitted from the symbol) is to be connected to the positive side of the circuit.
When you tune your radio, you will usually find that, as you turn the knob that changes the wavelength that you want to receive, you are changing the capacitance of a variable air-spaced capacitor just behind the knob. A variable capacitor can be represented by the symbol
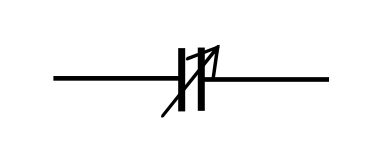
Such a capacitor often consists of two sets of interleaved partially overlapping plates, one set of which can be rotated with respect to the other, thus changing the overlap area and hence the capacitance. Thinking about this suggests to me a couple of small problems for you to amuse yourself with.
Problem 1.

\(\text{FIGURE V.26}\)
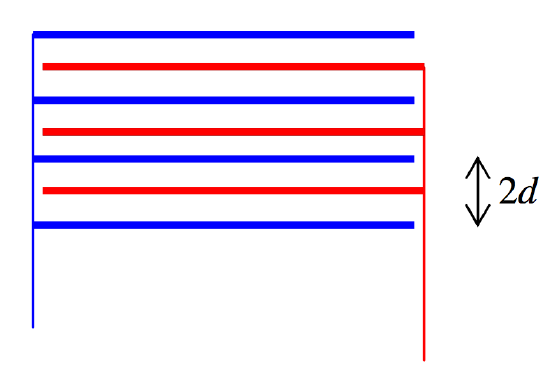
A capacitor (Figure \(V.\)26) is made from two sets of four plates. The area of each plate is A and the spacing between the plates in each set is 2d. The two sets of plates are interleaved, so that the distance between the plates of one set and the plates of the other is d. What is the capacitance of the system?
Problem 2
\(\text{FIGURE V.27}\)
This is just like Problem 1, except that one set has four plates and the other has three. What is the capacitance now?
Solutions. The answer to the first problem is 7\(\epsilon_0 A/d\) and the answer to the second problem is 6\(\epsilon_0 A/d\) – but it isn’t good enough just to assert that this is the case. We must give some reasons.
Let us suppose that the potential of the left-hand (blue) plates is zero and the potential of the right-hand (blue) plates is \(V.\) The electric field in each space is V/d and D = \(\epsilon\)0V/d. The surface charge density on each plate, by Gauss’s theorem, is therefore 2\(\epsilon\)0V/d except for the two end plates, for which the charge density is just \(\epsilon\)0V/d. The total charge held in the capacitor of Problem 1 is therefore \(\epsilon_0 AV/d + 3 \times 2\epsilon_0 AV/d = 7\epsilon_0 AV/d\), and the capacitance is therefore 7\(\epsilon_0 A/d\). For Problem 2, the blue set has two end-plates and two middle-plates, so the charge held is \(2 \times \epsilon_0 AV/d + 2 \times 2\epsilon_0 AV/d = 6\epsilon_0 AV/d\). The red set has three middle- plates and no end-plates, so the charge held is \(3 \times 2\epsilon_0 AV/d = 6\epsilon_0 AV/d\). The capacitance is therefore 6\(\epsilon_0 A/d\).


