2.1: Lorentz Force

Last updated
Save as PDF

Page ID: 24775

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Lorentz force is the force experienced by charge in the presence of electric and magnetic fields.

Consider a particle having charge \(q\). The force \({\bf F}_e\) experienced by the particle in the presence of electric field intensity \({\bf E}\) is

\[{\bf F}_e = q{\bf E} \nonumber \]

The force \({\bf F}_m\) experienced by the particle in the presence of magnetic flux density \({\bf B}\) is

\[{\bf F}_m = q{\bf v} \times {\bf B} \nonumber \]

where \({\bf v}\) is the velocity of the particle. The Lorentz force experienced by the particle is simply the sum of these forces; i.e.,

\[\begin{align} {\bf F} &= {\bf F}_e + {\bf F}_m \nonumber \\ &= q\left( {\bf E} + {\bf v} \times {\bf B} \right) \label{m0015_eLF}\end{align} \]

The term “Lorentz force” is simply a concise way to refer to the combined contributions of the electric and magnetic fields.

A common application of the Lorentz force concept is in analysis of the motions of charged particles in electromagnetic fields. The Lorentz force causes charged particles to exhibit distinct rotational (“cyclotron”) and translational (“drift”) motions. This is illustrated in Figures \(\PageIndex{1}\) and \(\PageIndex{2}\).

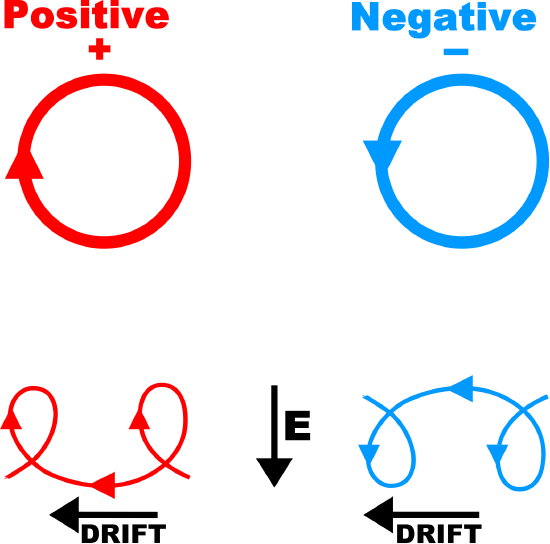Figure \(\PageIndex{1}\): Motion of a particle bearing (left) positive charge and (right) negative charge. Top: Magnetic field directed toward the viewer; no electric field. Bottom: Magnetic field directed toward the viewer; electric field oriented as shown. ( CC BY 2.5; Stannerd)

Figure \(\PageIndex{2}\): Electrons moving in a circle in a magnetic field (cyclotron motion). The electrons are produced by an electron gun at bottom, consisting of a hot cathode, a metal plate heated by a filament so it emits electrons, and a metal anode at a high voltage with a hole which accelerates the electrons into a beam. The electrons are normally invisible, but enough air has been left in the tube so that the air molecules glow pink when struck by the fast-moving electrons. ( CC BY-SA 4.0; M. Biaek)

Additional Reading:

“Lorentz force” on Wikipedia.