9.6: Far-Field Radiation from a Thin Straight Filament of Current
( \newcommand{\kernel}{\mathrm{null}\,}\)
A simple distribution of radiating current that is encountered in common practice is the thin straight current filament, shown in Figure 9.6.1.
 Figure 9.6.1: A thin straight distribution of radiating current. ( CC BY-SA 4.0; C. Wang)
Figure 9.6.1: A thin straight distribution of radiating current. ( CC BY-SA 4.0; C. Wang)
The defining characteristic of this distribution is that the current filament is aligned along a straight line, and that the maximum dimension of the cross-section of the filament is much less than a wavelength. The latter characteristic is what we mean by “thin” – i.e., the filament is “electrically thin.” Physical distributions of current that meet this description include the electrically-short dipole (Section 9.5) and the half-wave dipole (Section 9.7) among others. A gentler introduction to this distribution is via Section 9.5 (“Radiation from an Electrically-Short Dipole”), so students may want to review that section first. This section presents the more general case.
Let the magnitude and phase of current along the filament be given by the phasor quantity ˜I(z) (SI base units of A). In principle, the only constraint on ˜I(z) that applies generally is that it must be zero at the ends of the distribution; i.e., ˜I(z)=0 for |z|≥L/2. Details beyond this constraint depend on L and perhaps other factors. Nevertheless, the characteristics of radiation from members of this class of current distributions have much in common, regardless of L. These become especially apparent if we limit our scope to field points far from the current, as we shall do here.
There are two approaches that we might consider in order to find the electric field radiated by this distribution. The first approach is to calculate the magnetic vector potential ˜A by integration over the current distribution (Section 9.3), calculate ˜H=(1/μ)∇טA, and finally calculate ˜E from ˜H using the differential form of Ampere’s law. In this section, we shall employ a simpler approach, shown in Figure 9.6.2.
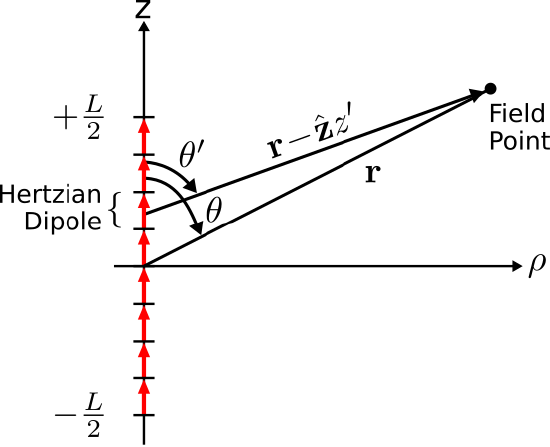 Figure 9.6.2: Current distribution approximated as a set of Hertzian dipoles. ( CC BY-SA 4.0; C. Wang)
Figure 9.6.2: Current distribution approximated as a set of Hertzian dipoles. ( CC BY-SA 4.0; C. Wang)
Imagine the filament as a collection of many shorter segments of current that radiate independently. The total field is then the sum of these short segments. Because these segments are very short relative to the length of the filament as well as being short relative to a wavelength, we may approximate the current over each segment as constant. In other words, we may interpret each segment as being, to a good approximation, a Hertzian dipole.
The advantage of this approach is that we already have a solution for every segment. In Section 9.4, it is shown that a ˆz-directed Hertzian dipole at the origin radiates the electric field
˜E(r)≈ˆθjη˜I(βΔl)4π (sinθ)e−jβrr
where ˜I and Δl may be interpreted as the current and length of the filament, respectively. In this expression, η is the wave impedance of medium in which the filament radiates (e.g., ≈377 Ω for free space), and we have presumed lossless media such that the attenuation constant α≈0 and the phase propagation constant β=2π/λ. This expression also assumes field points far from the filament; specifically, distances r that are much greater than λ. Repurposing this expression for the present problem, we note that the segment at the origin radiates the electric field:
˜E(r;z′=0)≈ˆθjη˜I(0)(βΔl)4π (sinθ)e−jβrr
where the notation z′=0 indicates the Hertzian dipole is located at the origin. Letting the length Δl of this segment shrink to differential length dz′, we may describe the contribution of this segment to the field radiated by the ESD as follows:
d˜E(r;z′=0)≈ˆθjη˜I(0)(βdz′)4π (sinθ)e−jβrr
Using this approach, the electric field radiated by any segment can be written:
d˜E(r;z′)≈ˆθ′jηβ˜I(z′)4π(sinθ′)e−jβ|r−ˆzz′||r−ˆzz′| dz′
Note that θ is replaced by θ′ since the ray r−ˆzz′ forms a different angle (i.e., θ′) with respect to ˆz. Subsequently, ˆθ is replaced by ˆθ′, which varies similarly with z′. The electric field radiated by the filament is obtained by integration over these contributions, yielding:
˜E(r)≈∫+L/2−L/2d˜E(ˆr;z′)
Expanding this expression:
˜E(r)≈jηβ4π∫+L/2−L/2ˆθ′˜I(z′) (sinθ′)e−jβ|r−ˆzz′||r−ˆzz′|dz′
Given some of the assumptions we have already made, this expression can be further simplified. For example, note that θ′≈θ since L≪r. For the same reason, ˆθ′≈ˆθ. Since these variables are approximately constant over the length of the filament, we may move them outside the integral, yielding:
˜E(r)≈ˆθjηβ4π (sinθ)∫+L/2−L/2˜I(z′)e−jβ|r−ˆzz′||r−ˆzz′|dz′
It is also possible to simplify the expression |r−ˆzz′|. Consider Figure 9.6.3.
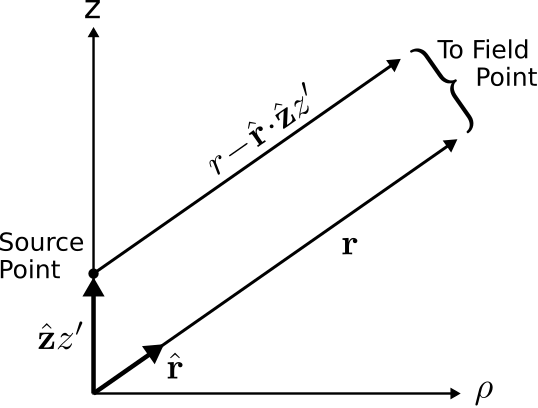 Figure 9.6.3: Parallel ray approximation. ( CC BY-SA 4.0; C. Wang)
Figure 9.6.3: Parallel ray approximation. ( CC BY-SA 4.0; C. Wang)
Since we have already assumed that r≫L (i.e., the distance to field points is much greater than the length of the filament), the vector r is approximately parallel to the vector r−ˆzz′. Subsequently, it must be true that
|r−ˆzz′|≈r−ˆr⋅ˆzz′≈r−z′cosθ
Note that the magnitude of r−ˆr⋅ˆzz′ must be approximately equal to r, since r≫L. So, insofar as |r−ˆzz′| determines the magnitude of ˜E(r), we may use the approximation:
|r−ˆzz′|≈r (magnitude)
Insofar as |r−ˆzz′| determines phase, we have to be more careful. The part of the integrand of Equation ??? that exhibits varying phase is e−jβ|r−ˆzz′|. Using Equation 9.6.8, we find
e−jβ|r−ˆzz′|≈e−jβre+jβz′cosθ
These simplifications are known collectively as a far field approximation, since they are valid only for distances “far” from the source.
Applying these simplifications for magnitude and phase to Equation ???, we obtain:
˜E(r)≈ˆθjηβ4πe−jβrr (sinθ) ⋅∫+L/2−L/2˜I(z′)e+jβz′cosθdz′
Finally, it is common to eliminate the factor of β in the magnitude using the relationship β=2π/λ, yielding:
˜E(r)≈ˆθjη2e−jβrr (sinθ) ⋅[1λ∫+L/2−L/2˜I(z′)e+jβz′cosθdz′]
The electric field radiated by a thin, straight, ˆz-directed current filament of length L located at the origin and aligned along the z axis is given by Equation 9.6.15. This expression is valid for r≫L and r≫λ.
At field points satisfying the conditions r≫L and r≫λ, the wave appears to be locally planar. Therefore, we are justified using the plane wave relationship ˜H=(1/η)ˆrטE to calculate ˜H.
As a check, one may readily verify that Equation 9.6.15 yields the expected result for the electrically-short dipole (Section 9.5).


