10.14: Friis Transmission Equation
( \newcommand{\kernel}{\mathrm{null}\,}\)
A common task in radio systems applications is to determine the power delivered to a receiver due to a distant transmitter. The scenario is shown in Figure 10.14.1:
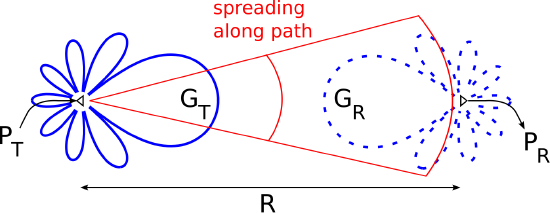 Figure 10.14.1: Copy and Paste Caption here
Figure 10.14.1: Copy and Paste Caption here
A transmitter delivers power PT to an antenna which has gain GT in the direction of the receiver. The receiver’s antenna has gain GR. As always, antenna gain is equal to directivity times radiation efficiency, so GT and GR account for losses internal to the antenna, but not losses due to impedance mismatch.
A simple expression for PR can be derived as follows. First, let us assume “free space conditions”; that is, let us assume that the intervening terrain exhibits negligible absorption, reflection, or other scattering of the transmitted signal. In this case, the spatial power density at range R from the transmitter which radiates this power through a lossless and isotropic antenna would be:
PT4πR2
that is, total transmitted power divided by the area of a sphere of radius R through which all the power must flow. The actual power density Si is this amount times the gain of the transmit antenna, i.e.:
Si=PT4πR2GT
The maximum received power is the incident co-polarized power density times the effective aperture Ae of the receive antenna:
PR,max=AeSico=AePT4πR2GT
This assumes that the receive antenna is co-polarized with the incident electric field, and that the receiver is conjugate-matched to the antenna. The effective aperture can also be expressed in terms of the gain GR of the receive antenna:
Ae=λ24πGR
Thus, Equation 10.14.3 may be written in the following form:
PR,max=PTGT(λ4πR)2GR
This is the Friis transmission equation. Summarizing:
The Friis transmission equation (Equation ???) gives the power delivered to a conjugate-matched receiver in response to a distant transmitter, assuming co-polarized antennas and free space conditions.
The factor (λ/4πR)2 appearing in the Friis transmission equation is referred to as free space path gain. More often this is expressed as the reciprocal quantity:
Lp≜(λ4πR)−2
which is known as free space path loss. Thus, Equation ??? may be expressed as follows:
PR,max=PTGTL−1pGR
The utility of the concept of path loss is that it may also be determined for conditions which are different from free space. The Friis transmission equation still applies; one simply uses the appropriate (and probably significantly different) value of Lp.
A common misconception is that path loss is equal to the reduction in power density due to spreading along the path between antennas, and therefore this “spreading loss” increases with frequency. In fact, the reduction in power density due to spreading between any two distances R1<R2 is:
PT/4πR21PT/4πR22=(R1R2)2
which is clearly independent of frequency. The path loss Lp, in contrast, depends only on the total distance R and does depend on frequency. The dependence on frequency reflects the dependence of the effective aperture on wavelength. Thus, path loss is not loss in the traditional sense, but rather accounts for a combination of spreading and the λ2 dependence of effective aperture that is common to all receiving antennas.
Finally, note that Equation ??? is merely the simplest form of the Friis transmission equation. Commonly encountered alternative forms include forms in which GT and/or GR are instead represented by the associated effective apertures, and forms in which the effects of antenna impedance mismatch and/or cross-polarization are taken into account.
Terrestrial telecommunications systems commonly aggregate large numbers of individual communications links into a single high-bandwidth link. This is often implemented as a radio link between dish-type antennas having gain of about 27 dBi (that’s dB relative to a lossless isotropic antenna) mounted on very tall towers and operating at frequencies around 6 GHz. Assuming the minimum acceptable receive power is −120 dBm (that’s −120 dB relative to 1 mW; i.e., 10−15 W) and the required range is 30 km, what is the minimum acceptable transmit power?
Solution
From the problem statement:
GT=GR=1027/10≅501
λ=cf≅3×108 m/s6×109 Hz≅5.00 cm
R=30 km, and PR≥10−15 W. We assume that the height and high directivity of the antennas yield conditions sufficiently close to free space. We further assume conjugate-matching at the receiver, and that the antennas are co-polarized. Under these conditions, PR=PR,max and Equation ??? applies. We find:
PT≥PR,maxGT(λ/4πR)2GR≅2.26×10−7 W≅2.26×10−4 mW≅−36.5 dBm_
Additional Reading:
- “Free-space path loss” on Wikipedia.
- “Friis transmission equation” on Wikipedia.


