9.5: Exercises
- Page ID
- 34570
Exercise \(\PageIndex{1}\)
Is the concept of a contour integral well-defined if the integrand \(f(z)\) is non-differentiable along the contour? Why or why not?
Exercise \(\PageIndex{2}\)
In Section 9.4, we dealt with the integral \[\int_{-\infty}^\infty \frac{dx}{x^2 + 1}.\] Redo this calculation, but this time close the contour in the lower half-plane. Show that the result is the same.
- Answer
-
By analytic continuation, consider the integral \[I = \oint \frac{dz}{z^4 + 1},\] where the contour is closed in the upper half-plane (we could also choose to close below without changing the results). The contour integral over the large arc scales with the arc radius \(R\) as \(R^{-3}\), so it vanishes as \(R \rightarrow \infty\). Hence, \(I\) is exactly equal to the definite integral we are after.
To evaluate the loop integral, we need the poles of the integrand, which are the solutions to \(z^4 = -1\). Writing \(-1 = \exp(i\pi)\), we find that the roots are \(\exp(i\pi/4) \times \{\text{4-roots of unity}\}.\) These can be written in the Cartesian representation as \[\begin{align} z_1 &= \frac{1+i}{\sqrt{2}} \\ z_2 &= \frac{-1+i}{\sqrt{2}} \\ z_3 &= \frac{-1-i}{\sqrt{2}} \\ z_4 &= \frac{1-i}{\sqrt{2}}.\end{align}\] By closing the contour above, we enclose \(z_1\) and \(z_2\). Thus, by the residue theorem, \[\begin{align} I &= 2\pi i \left\{\left[\mathrm{Res} \left(\frac{1}{z^4 + 1}\right)\right]_{z=z_1} + \left[\mathrm{Res} \left(\frac{1}{z^4 + 1}\right)\right]_{z=z_2}\right\} \\ &= 2\pi i\left[\frac{1}{(z_1-z_2)(z_1-z_3)(z_1-z_4)} + \frac{1}{(z_2-z_1)(z_2-z_3)(z_2-z_4)}\right] \\ &= 2\pi i \left[\frac{\sqrt{8}}{(2)(2+2i)(2i)} + \frac{\sqrt{8}}{(-2)(2i)(-2+2i)}\right] \\ &= \frac{\sqrt{2}\pi i}{2} \left[\frac{1}{-1+i} + \frac{1}{1+i}\right] \\ &= \frac{\pi}{\sqrt{2}}.\end{align}\]
Exercise \(\PageIndex{3}\)
Calculate \[\int_{-\infty}^\infty dx\; \frac{1}{x^4 + 1}.\]
Exercise \(\PageIndex{4}\)
Calculate \[\int_{-\infty}^\infty dx\; \left[\frac{\sin(x)}{x}\right]^2.\]
Exercise \(\PageIndex{5}\)
Calculate \[\int_0^\infty dx \frac{x^{\lambda}}{x+1}, \;\;\mathrm{where}\; -1 < \lambda < 0.\] Hint: place the integrand’s branch cut along the positive real axis.
Exercise \(\PageIndex{6}\)
Solve the definite integral \[I = \int_0^{2\pi} \frac{d\phi}{\cos\phi+3},\] via the following steps. First, show that along a unit circle in the complex plane centered at the origin, \[\cos\phi = \frac{1}{2}\left(z+\frac{1}{z}\right),\] where \(z(\phi) = \exp(i\phi)\). Then define a complex function \(f(z)\) such that the loop integral \(\oint f(z) \;dz,\) taken over the circular contour, is equal to \(I\). Hence, calculate \(I\).
- Answer
-
A unit circle centered at the origin can be parameterized by \(z = \exp(i\phi)\). Hence, along this circle, \[\begin{align} \cos\phi &= \frac{1}{2}\left(e^{i\phi} + e^{-i\phi}\right) \\ &= \frac{1}{2} \left(e^{i\phi} + \frac{1}{e^{i\phi}}\right) \\ &= \frac{1}{2}\left(z + \frac{1}{z}\right).\end{align}\] Also, \[\frac{dz}{d\phi} = iz.\] Let us denote this circular contour by \(\Gamma\). We want to find a function \(f(z)\) such that \[\oint_\Gamma f(z) \;dz = \int_0^{2\pi} \frac{d\phi}{\cos\phi+3}.\] The contour integral on the left side can be parameterized as \[\int_0^{2\pi} d\phi\; f\big(z(\phi)\big)\, \frac{dz}{d\phi}.\] Therefore, we want \(f(z)\) such that \[\begin{align} f\big(z(\phi)\big) \frac{dz}{d\phi} &= \frac{1}{\cos\phi+3} \\ = f(z) \;\,(i z) &= \frac{1}{\frac{1}{2}\left(z+\frac{1}{z}\right) + 3}.\end{align}\] After some algebra, we obtain \[f(z) = \frac{-2i}{z^2 + 6z + 1}.\] The denominator in \(f(z)\) has two roots, which are both real: \[\begin{align} z_+ &= -3 + 2\sqrt{2} = - 0.17157\dots \\ z_- &= -3 - 2\sqrt{2} = -5.8284\dots\end{align}\] Only the \(z_+\) pole is enclosed by the unit circle. Thus, we can use the residue theorem to evaluate the integral: \[\begin{align} I = \oint_\Gamma \frac{-2i}{z^2 + 6z + 1} \, dz &= 2\pi i \; \mathrm{Res}\left[\frac{-2i}{(z-z_+)(z-z_-)}\right]_{z = z_+} \\ &= 2\pi i \left(\frac{-2i}{z_+-z_-}\right) \\ &= \frac{4\pi}{\left(-3 + 2\sqrt{2}\right)-\left(-3 - 2\sqrt{2}\right)} \\ &= \frac{\pi}{\sqrt{2}}.\end{align}\]
Exercise \(\PageIndex{7}\)
Suppose \(f(z)\) is analytic everywhere in the upper half-plane, including the real line, and that its magnitude vanishes as \(1/|z|\) or faster as \(|z| \rightarrow \infty\). Find the value of the principal-value integral \[\mathcal{P}\left[\int_{-\infty}^\infty \frac{f(x)}{x-a} dx \right],\] where \(a\) is some real constant. Hence, prove that the real and imaginary parts of \(f\) along the real line are related by \[\begin{align} \mathrm{Re}\big[f(x)\big] &= \;\;\,\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Im}[f(w)]}{w-x} dw\right] \\ \mathrm{Im}\big[f(x)\big] &= -\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Re}[f(w)]}{w-x} dw\right]. \end{align}\] These are called the Kramers-Kronig relations. In physics, these relations impose important constraints on the frequency dependence of the real and imaginary parts of the dielectric function (the square of the complex refractive index).
- Answer
-
To evaluate the principal-value integral \[I = \mathcal{P}\left[\int_{-\infty}^\infty \frac{f(x)}{x-a} dx \right],\] we introduce the following loop contour:
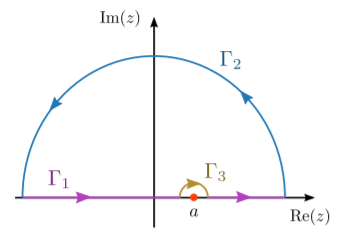
Figure \(\PageIndex{1}\) The solution procedure is very similar to the example worked out in Section 9.4. From the properties of \(f(z)\) given in the problem statement, we can conclude that (i) the integrand is analytic on and within the loop contour, so the residue theorem can be used; and (ii) the integrand vanishes quickly enough far from the origin so that, by Jordan’s lemma, the integral over \(\Gamma_2\) vanishes. Hence, \[I = i \pi f(a).\] By relabelling the dummy variables \(x \rightarrow y\) and \(a \rightarrow x\), we can write \[f(x) = -\frac{i}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{f(y)}{y-x} dy \right].\] Let us now break up \(f\) into its real and imaginary parts: \[\begin{align} \mathrm{Re}[f(x)] + i \mathrm{Im}[f(x)] &= -\frac{i}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Re}[f(y)] + i \mathrm{Im}[f(y)]}{y-x} \;dy \right] \\ &= \frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Im}[f(y)] -i\mathrm{Re}[f(y)]}{y-x} \;dy \right].\end{align}\] Equating the real and imaginary parts of the two sides, we obtain the following two real equations, which are the Kramers-Kronig relations: \[\begin{align} \mathrm{Re}[f(x)] &= \;\;\,\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Im}[f(y)]}{y-x} \;dy \right] \\ \mathrm{Im}[f(x)] &= -\frac{1}{\pi} \mathcal{P}\left[\int_{-\infty}^\infty \frac{\mathrm{Re}[f(y)]}{y-x} \; dy \right].\end{align}\]


