3.1: A Model of Computing

A modern computer is a tremendously complex system, with many things to understand at the level of the hardware, the operating system, and the programming software (e.g. Python). It is helpful to consider a simplified computing model, which is basically a "cartoon" representation of a computer that omits the unimportant facts about how it operates, and focuses on the most important aspects of what a computer program does.

The standard paradigm of computing that we use today is the Von Neumann architecture, which divides a computer into three inter-connected units: processor, memory, and input/output devices. We'll use this as the basis of our simplified model, with an emphasis on the processor and memory parts.

A computer's memory is essentially a chunk of space where we can store numbers. For now, we won't concern ourselves with how the contents of memory are organized or formatted. The processor can read one or more numbers from any locations (or addresses) in memory, perform some basic operations on them, and then write the results into any other addresses. We also make three other important assumptions:

1. The capacity is effectively infinite; we don't worry about running out.
2. The memory is random-access memory (RAM), meaning that the processor can access any addresses in memory, one after another, with the same speed. (In real life, not all types of memory are random-access. Disk drives, for instance, are not, because the scanning head must physically move to different positions in order to read different parts of memory. However, ordinary computer programs can ignore such details, which are left to the operating system to manage.)
3. The processor can only do one thing at a time. For example, if you ask it to read two numbers from memory, that takes twice as long as reading a single number from memory. (Again, real computers violate this assumption to some extent; computers now commonly have multiple processors that can performs multiple operations simultaneously. Our present simple model ignores these complications.)

A program is a set of instructions for the processor. For example, the following line of code is a program (or part of a program) that tells the processor to add up four numbers that are currently stored in memory, and save the result to another memory address labeled x:

x = a + b + c + d

Because the processor can only do one thing at a time, even a simple line of code like this involves several sequential steps. The processor can't simultaneously read all four memory addresses (corresponding to a through d); it must read them one at a time. The following figure shows how the processor might carry out the above addition program:

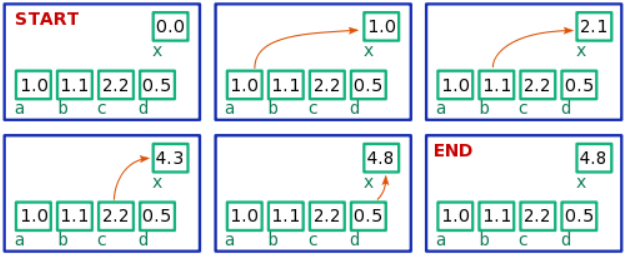
Figure \(\PageIndex{1}\): A sequence of steps for adding up four numbers, x = a + b + c + d. The computer's memory is visualized as a blue box; the variables x and a through d correspond to addresses in memory, shown as smaller green boxes containing numbers. The processor performs the additions one at a time.