10.4: Adams-Moulton Method
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the Second-Order Adams-Moulton (AM2) method, we take
→yn+1=→yn+h2[→F(→yn,tn)+→F(→yn+1,tn+1)].
Conceptually, the derivative term here is the average of the Forward Euler and Backward Euler derivative terms. Because →yn+1 appears on the right-hand side, this is an implicit method. Thus, like the Backward Euler Method, it typically has to be solved iteratively, but is numerically stable. The advantage of the AM2 method is that its local truncation error is substantially lower. To see this, let us take the derivative of both sides of the ODE over one time step:
∫tn+1tnd→ydtdt=∫tn+1tn→F(→y(t),t)dt
The integral on the left-hand side reduces to →yn+1−→yn. As for the integral on the right-hand side, if we perform this integral numerically using the trapezium rule, then the result is the derivative term in the AM2 formula. The local truncation error is given by the numerical error of the trapezium rule, which is O(h3). That's an improvement of one order compared to the Euler methods. (Based on this argument, we can also see that the Forward Euler method and the Backward Euler methods involve approximating the integral on the right-hand side using a rectangular area, with height given by the value at tn and tn+1 respectively. From this, it's clear why the AM2 scheme gives better results.)
There are also higher-order Adams-Moulton methods, which generate even more accurate results by also sampling the derivative function at previous steps: F(→yn−1,tn−1), F(→yn−2,tn−2), etc.
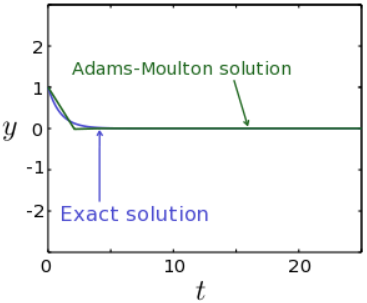
In Fig. 10.4.1, we plot the AM2 solution for the problem dy/dt=−κy(t), using the same parameters (including the same step size h) as in Fig. 10.2.1 (Forward Euler Method) and Fig. 10.3.1 (Backward Euler Method). It is clear that the AM2 results are significantly more accurate.


