1.3: Lorentz Transformation
( \newcommand{\kernel}{\mathrm{null}\,}\)
The time dilation and length contraction relationships actually have very limited applicability. To use the time dilation relationship, one of the two observers must measure a proper time, where the two events occur at exactly the same spatial point. To use the length contraction relationship, one of the two observers must measure a proper length, where the two events must be at rest with respect to the observer. What if you want to compare measurements concerning more general events? To do this requires the Lorentz Transformation, which allows you to transform the spacetime coordinates of an event in one inertial reference system to any other inertial reference system.
To derive the Lorentz transformation, imagine two inertial reference systems, labeled O and O′. Let the origins of O and O′ overlap at time zero, and allow O′ to move with speed u relative to O. (Therefore, at a later time t, the origins are separated by a distance ut). Call the direction of motion the x-direction.
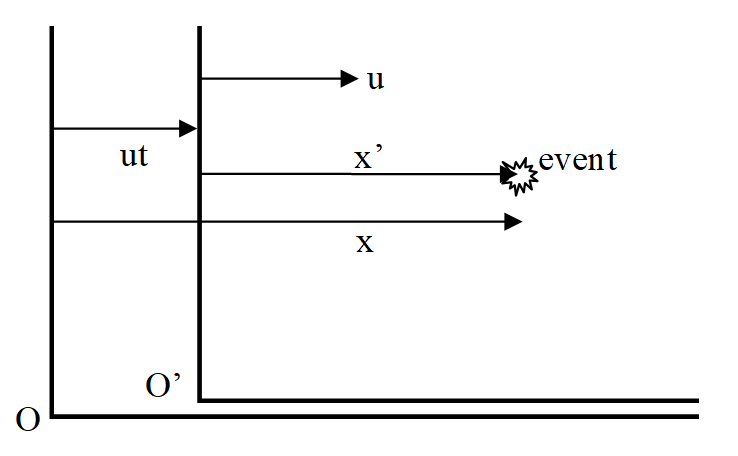
Figure 1.3.1:
Now imagine an event that occurs somewhere in spacetime. This event is located at position x relative to the O system, and position x′ relative to the O′ system. How are these two locations related?
You may be tempted to state that
x=x′+ut
however, this can’t be correct because x and x′ are measured in different reference systems. However, imagine that the event is the tip of a meterstick, fixed in O’, striking some object. Since x′ is now a proper length in O′, it will appear contacted in O by the gamma factor. Therefore, the correct relationship between x and x′ is
x=x′γ+ut
rearranging yields
x′=γ(x−ut)
Since there is no relative motion in the y and z directions, these positions are the same in both coordinate systems
y′=y
z′=z
This completes the spatial part of the Lorentz transformation, but what about the temporal part? To determine how t and t′ are related, now imagine that the event under investigation is the result of a light pulse, emitted from the origin when the two origins overlapped at time zero, striking some detector. Since the speed of light is the same in both systems, the distance measured in each system must be equal to the product of c and the elapsed time
x′=γ(x−ut)
ct′=γ(ct−uxc)
t′=γ(t−uxc2)
Using the Lorentz Transformation
Inside of a spaceship zooming past earth at 0.5c, I fire a laser (in the same direction as the ship’s motion) and let it strike a mirror 10 m in front of the laser.
- What is the elapsed time measured on the earth between turning on the laser and the light striking the mirror?
- How far has the light traveled before hitting the mirror, as measured on earth?
Since neither the earth’s observers nor the observers on the ship measure a proper time or a proper length between the two events (turning on the laser and the laser striking the mirror), a more general method of relating different observers’ measurements is needed. This general method of relating measurements is the Lorentz Transformation. The Lorentz Transformation relates the coordinates of a spacetime event, (x,y,z,t), measured in one frame to the coordinates of the same event in a frame moving with relative velocity u, (x′,y′,z′,t′) as follows:
x′=γ(x−ut)
y′=y
z′=z
t′=γ(t−uxc2)
These equations are written in a form that easily allows the determination of the primed coordinates from the unprimed. If the situation requires the inverse of this task, the equations can be easily inverted (by changing the sign of u and flipping the primed and unprimed notation) to yield
x=γ(x′−ut′)
y=y′
z=z′
t=γ(t′−ux′c2)
Let the two coordinate systems overlap at the first event (the laser is fired). Thus, the position and time of the laser’s firing is zero in both coordinate systems. We now must find the position and time of the second event (the laser strikes the mirror). This is relatively easy to determine in the frame of the spaceship (the primed frame):
x′=10m
t′=10mc≈3.33×10−8s
Since we know the spacetime location of the event in the primed frame, the Lorentz Transformation allows us to transform this information into the earth frame. With u=0.5c (γ=1.155),
t=γ(t′+ux′c2)=1.155((10c)+(0.5c)(10)c2)=17.3mc=5.7×10−8s
and for the x-direction
x=γ(x′+ut′)=1.155(10+(0.5c)(10c))=17.3m
The light travels 17.3m and takes 5.78×10−8s to strike the mirror in the earth’s frame.


