Skip to main content
Physics LibreTexts

27.1: Introduction

  1. Last updated
  2. Save as PDF
  • Page ID
    16199

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    learning objectives

    • Explain why the Galilean invariance didn’t work in Maxwell’s equations

    Galilean invariance or Galilean relativity states that the laws of motion are the same in all inertial (or non-accelerating) frames. Galileo Galilei first described this principle in 1632 using the example of a ship travelling at constant velocity, without rocking, on a smooth sea; any observer doing experiments below the deck would not be able to tell whether the ship was moving or stationary. The fact that the Earth orbits around the sun at approximately 30 km/s offers a somewhat more dramatic example, though it is technically not an inertial reference frame.

    Specifically, the term Galilean invariance today usually refers to this principle as applied to Newtonian mechanics—that is, Newton’s laws hold in all inertial frames. In this context it is sometimes called Newtonian relativity. Among the axioms from Newton’s theory are:

    • There exists an absolute space in which Newton’s laws are true. An inertial frame is a reference frame in relative uniform motion to absolute space.
    • All inertial frames share a universal (or absolute) time.

    Derivation

    Galilean relativity can be shown as follows. Consider two inertial frames S and S’. A physical event in S will have position coordinates r = (x, y, z) and time t; similarly for S’. By the second axiom above, one can synchronize the clock in the two frames and assume t = t‘. Suppose S’ is in relative uniform motion to S with velocity v. Consider a point object whose position is given by r = r(t) in S. We see that

    \[\mathrm { r } ^ { \prime } ( \mathrm { t } ) = \mathrm { r } ( \mathrm { t } ) - \mathrm { vt }\]

    This transformation of variables between two inertial frames is called Galilean transformation. Now, the velocity of the particle is given by the time derivative of the position:

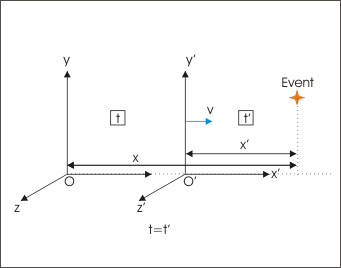
    image

    Galilean Invariance: Newtonian mechanics is invariant under a Galilean transformation between observation frames (shown). This is called Galilean invariance.

    \[\mathrm { u } ^ { \prime } ( \mathrm { t } ) = \frac { \mathrm { d } } { \mathrm { d } t } \mathrm { r } ^ { \prime } ( \mathrm { t } ) = \frac { \mathrm { d } } { \mathrm { d } t } \mathrm { r } ( \mathrm { t } ) - \mathrm { v } = \mathrm { u } ( \mathrm { t } ) - \mathrm { v }\]

    Another differentiation gives the acceleration in the two frames:

    \[\mathrm { a } ^ { \prime } ( \mathrm { t } ) = \frac { \mathrm { d } } { \mathrm { dt } } \mathrm { u } ^ { \prime } ( \mathrm { t } ) = \frac { \mathrm { d } } { \mathrm { dt } } \mathrm { u } ( \mathrm { t } ) - 0 = \mathrm { a } ( \mathrm { t } )\]

    It is this simple but crucial result that implies Galilean relativity. Assuming that mass is invariant in all inertial frames, the above equation shows that Newton’s laws of mechanics, if valid in one frame, must hold for all frames. But it is assumed to hold in absolute space, therefore Galilean relativity holds.

    Issues

    Both Newtonian mechanics and the Maxwell’s equations were well established by the end of the 19th century. The puzzle lied in the fact that the Galilean invariance didn’t work in Maxwell’s equations. That is, unlike Newtonian mechanics, Maxwell’s equations are not invariant under a Galilean transformation. Albert Einstein’s central insight in formulating special relativity was that, for full consistency with electromagnetism, mechanics must also be revised, such that Lorentz invariance (introduced later) replaces Galilean invariance. At the low relative velocities characteristic of everyday life, Lorentz invariance and Galilean invariance are nearly the same, but for relative velocities close to that of light they are very different.

    Einstein’s Postulates

    Special relativity is based on Einstein’s two postulates: the Principle of Relativity and the Principle of Invariant Light Speed.

    learning objectives

    • Identify two postulates forming the foundation of special relativity

    In the late 19th century, the Newtonian mechanics was considered to be valid in all inertial frames of reference, which are moving at a constant relative velocity with respect to each other. (See our previous lesson on “Galilean-Newtonian Relativity. “) One issue, however, was that another well-established theory, the laws of electricity and magnetism represented by Maxwell’s equations, was not “invariant” under Galilean transformation—meaning that Maxwell’s equations don’t maintain the same forms for different inertial frames. In his “Special Theory of Relativity,” Einstein resolved the puzzle and broadened the scope of the invariance to extend the validity of all physical laws, including electromagnetic theory, to all inertial frames of reference.

    image

    Albert Einstein: Albert Einstein, a true pioneer of modern physics. His work on relativity, gavity, quantum mechanics, and statistical physics revolutionized physics.

    Einstein’s Postulates

    With two deceptively simple postulates and a careful consideration of how measurements are made, Einstein produced the theory of special relativity.

    1. The Principle of Relativity: The laws of physics are the same and can be stated in their simplest form in all inertial frames of reference.

    This postulate relates to reference frames. It says that there is no preferred frame and, therefore, no absolute motion.

    2. The Principle of Invariant Light Speed: The speed of light c is a constant, independent of the relative motion of the source and observer.

    The laws of electricity and magnetism predict that light travels at c = 2.998×108 m/s in a vacuum, but they do not specify the frame of reference in which light has this speed. Physicists assumed that there exists a stationary medium for the propagation of light, which they called ” luminiferous aether. ” In 1887, Michelson and Morley attempted to detect the relative motion of the Earth through the stationary luminiferous aether, but their negative results implied the speed of light c is independent of the motion of the source relative to the observer. Einstein accepted the result of the experiment and incorporated it in his theory of relativity.

    This postulate might sound easy to accept, but it is rather counterintuitive. Imagine that you can throw a baseball at a speed v (relative to you). If you are on a train moving at a speed V and throw a ball in the direction of the train’s movement, the baseball will travel at a speed v+V for an observer stationary on the ground.

    Now, instead of a baseball, let’s say you have a laser pointer. You turn on the laser pointer while you are on a moving train. What would be the speed of light from the laser pointer for a stationary observer on the ground? Our intuition says that it should be c+V. However, Einstein says that it should be only c!

    The Speed of Light

    The speed of light in vacuum is a universal physical constant crucial to many areas of physics.

    learning objectives

    • Discuss the invariance of the speed of light and identify the value of that speed in vacuum

    The speed of light in vacuum, commonly denoted c, is a universal physical constant that is crucial to many areas of physics. Its value is 299,792,458 m/s; this is a precise known value because the length of the meter is itself derived from this constant and the international standard for time. According to special relativity, c is the maximum speed at which all energy, matter, and information in the universe can travel. It is the speed at which all massless particles and associated fields (including electromagnetic radiation such as light) travel in vacuum. It is also the speed of gravity (i.e., of gravitational waves) predicted by current theories. Such particles and waves (including light) travel at c regardless of the motion of the source or the inertial frame of reference of the observer. In the theory of relativity, c interrelates space and time in the Lorentz transformation; it also appears in the famous equation of mass-energy equivalence: E = mc2.

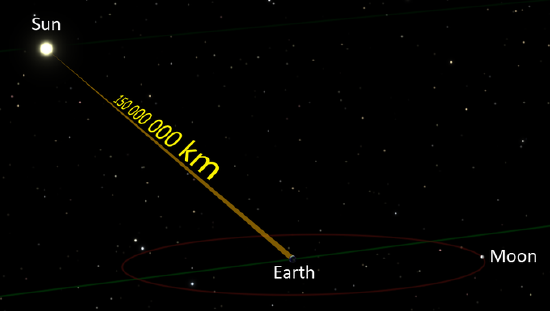
    image

    Sunlight’s Flight to Earth: Sunlight takes about 8 minutes and 19 seconds to reach the earth (based on the average distance between the sun and the earth)

    First Measurement

    The first quantitative estimate of the speed of light was made in 1676 by Rømer. From the observation that the periods of Jupiter’s innermost moon (Io) appeared to be shorter when Earth was approaching Jupiter than when it was moving away, he concluded that light travels at a finite speed. He estimated that it takes light 22 minutes to cross the diameter of Earth’s orbit. Christiaan Huygens combined this estimate with an estimate for the diameter of the Earth’s orbit to obtain an estimate of the speed of light of 220,000 km/s, 26 percent lower than the actual value.

    Fundamental Role in Physics

    The speed at which light waves propagate in vacuum is independent both of the motion of the wave source and of the inertial frame of reference of the observer. This invariance of the speed of light was postulated by Einstein in 1905 after being motivated by Maxwell’s theory of electromagnetism and the lack of evidence for “luminiferous aether”; it has since been consistently confirmed by many experiments.

    Key Points

    • Galilean invariance states that Newton’s laws hold in all inertial frames.
    • Newtonian mechanics assumes that there exists an absolute space and that time is universal.
    • Albert Einstein’s central insight in formulating special relativity was that, for full consistency with electromagnetism, mechanics must also be revised such that Lorentz invariance (introduced later) replaces Galilean invariance.
    • The special theory of relativity explores the consequences of the invariance of c with the assumption that the laws of physics are the same in all inertial frames of reference.
    • Einstein’s first postulate says that the laws of physics are the same and can be stated in their simplest form in all inertial frames of reference. It means that there is no preferred frame and, therefore, no absolute motion.
    • The speed of light c is a constant, independent of the relative motion of the source and observer.
    • The speed at which light waves propagate in vacuum is independent both of the motion of the wave source and of the inertial frame of reference of the observer. This invariance of the speed of light was postulated by Einstein in 1905 in his work on special relativity.
    • The value of the speed of light is 299,792,458 m/s; this is a precise known value because the length of the meter is itself derived from this constant and the international standard for time.
    • c is the maximum speed at which all energy, matter, and information in the universe can travel.

    Key Terms

    • Lorentz invariance: First introduced by Lorentz in an effort to explain how the speed of light was observed to be independent of the reference frame, and to understand the symmetries of the laws of electromagnetism.
    • absolute space: A concept introduced by Newton that assumes space remains always similar and immovable.
    • Maxwell’s equations: A set of equations describing how electric and magnetic fields are generated and altered by each other and by charges and currents.
    • special relativity: A theory that (neglecting the effects of gravity) reconciles the principle of relativity with the observation that the speed of light is constant in all frames of reference.
    • luminiferous aether: Light-bearing aether; the postulated medium for the propagation of light.
    • Lorentz transformation: a transformation relating the spacetime coordinates of one frame of reference to another in special relativity

    LICENSES AND ATTRIBUTIONS

    CC LICENSED CONTENT, SHARED PREVIOUSLY

    CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

    27.1: Introduction is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.