7.1: The Simplified Nuclear Potential Well
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}The nucleus is held together by the strong nuclear force. The strong force is a short range (~1 fm), very strong (~100 times stronger than the electromagnetic force), attractive force that acts between protons and neutrons. Rather than focus of the force, we will focus on the potential energy well associated with this force. Conveniently, this potential well is, to a reasonable approximation, a finite three-dimensional square well.
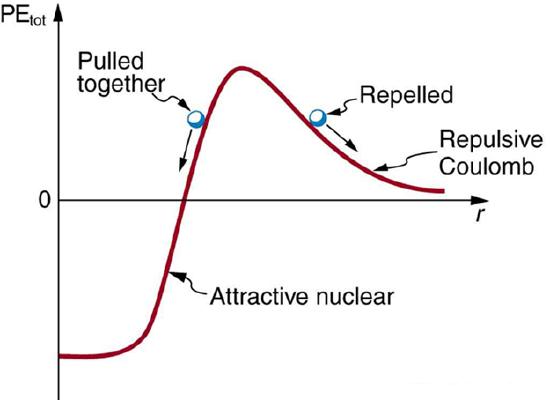
In addition to the strong force, the electromagnetic force also acts within the nucleus (as does the weak force, which we will ignore for now). Of course, the electromagnetic force acts only on the protons, not the neutrons, in the nucleus. Thus, the nuclear potential well looks slightly different for neutrons and protons, as illustrated below:
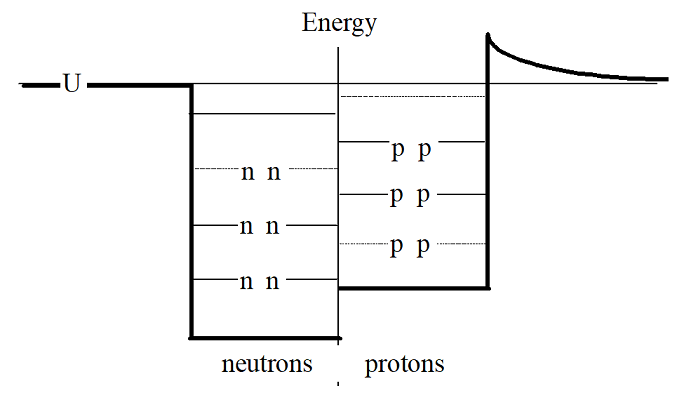
Typically, this will be drawn with half the well for neutrons and half for protons. (Of course, this is just a representation of the nuclear well, it isn’t actually split like this!) The difference in energy levels between neutrons and protons grows more and more pronounced as more and more particles are added to the nucleus. For example, a nucleus with 12 particles would look like this:

Notice that the particles fill the lowest available energy levels, six in the neutron well and six in the proton well resulting in \ce{^{12}C}. For a nucleus with 56 particles, however, the well looks more like this:
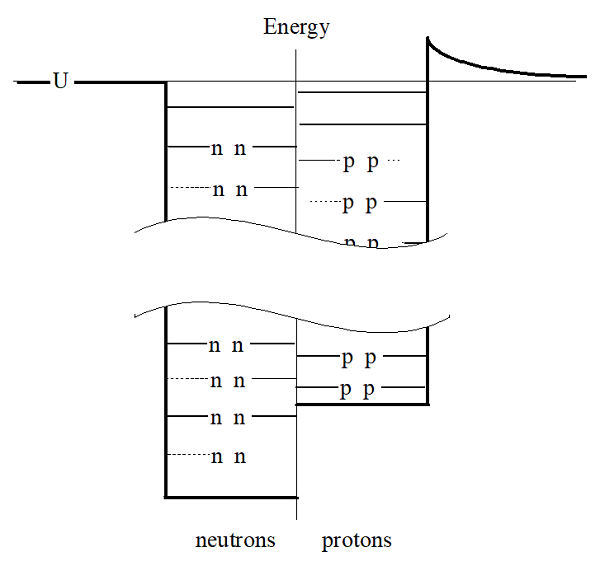
In this well, there are an “extra” four neutrons because the neutron well is substantially deeper than the proton well. This nucleus would have 30 neutrons and 26 protons, making it \ce{^{56}Fe}. This difference in well depth for protons and neutrons is why light nuclei typically have equal numbers of protons and neutrons while heavier nuclei have an overabundance of neutrons. This difference in well depth will also help us later to understand a type of radioactive decay termed beta decay.
In addition to the shape, the size and depth of the nuclear well can be easily estimated. The radius of a nucleus can be determined from the relationship:
r = (1.2 \,fm) A^{1/3}
where A is the total number of nucleons (protons and neutrons) in the nucleus.
An estimate of the depth of the well can be determined by calculating the total binding energy of the nucleus. This is the amount of energy that would be needed to remove each nucleon from the well. Surprisingly, the mass of the constituents of a nucleus is larger when the constituents are free (outside of the well) than when they are bound (inside the well). Thus, the total binding energy can be calculated by finding the mass difference between the bound-state nucleus and the total mass of its free nucleons, and converting this mass difference into an energy difference.
\text{Binding Energy} = \text{(mass of individual nucleons – mass of bound nucleus)}c^2 \label{BE}
One complication with calculating binding energy via Equation \ref{BE} is that only atomic masses are tabulated, while the difference in nuclear masses determines binding energy. To convert atomic masses to nuclear masses, multiples of the electron mass must be subtracted from each term.
\text{Binding Energy} = \text{(mass of individual nucleons – mass of bound nucleus - mass of bound electrons)}c^2 \label{BE1}
Example \PageIndex{1}
What is the nuclear binding energy of \ce{^4_2He}?
Solution
This is a simple application of Equation \ref{BE1}
\begin{align*} BE &= \left[ (2m_{proton} - 2m_{neutron}) - (m_{He, atomic} - 2 m_{electron}) \right ] c^2 \\[5pt] &= \left[ (2 ( 1.00727g\,u) - 2(1.008665\, u) - 4.002603\,u + 2(0.000549\,u) \right] c^2 \\[5pt] &= (0.030377\,u ) c^2 \\[5pt] &= 0.030377 ( 931.5 \,MeV) \\[5pt] &= 28.3\, MeV \end{align*}
Thus, 28.3 MeV would be needed to full disassemble a nucleus.
Rather than the total binding energy, the binding energy per nucleon is often calculated. This is simply the total binding energy divided by the number of nucleons in the nucleus. Thus, for helium-4, the binding energy per nucleon is:
\begin{align*} BE_{per\, nucleon} &= \dfrac{BE}{A} \\[5pt] &=\dfrac{28.3\,MeV}{4} \\[5pt] &= 7.08 \,MeV \end{align*}
The graph of binding energy per nucleon has the interesting property that a natural maximum occurs for \ce{^{62}Ni}. This means that \ce{^{62}Ni} nuclei are the most tightly bound nuclei. Additionally, nuclei with fewer nucleons can become more tightly bound (and release large amounts of energy) through the process of fusion, and nuclei with more nucleons can become more tightly bound (and release large amounts of energy) through the process of fission.
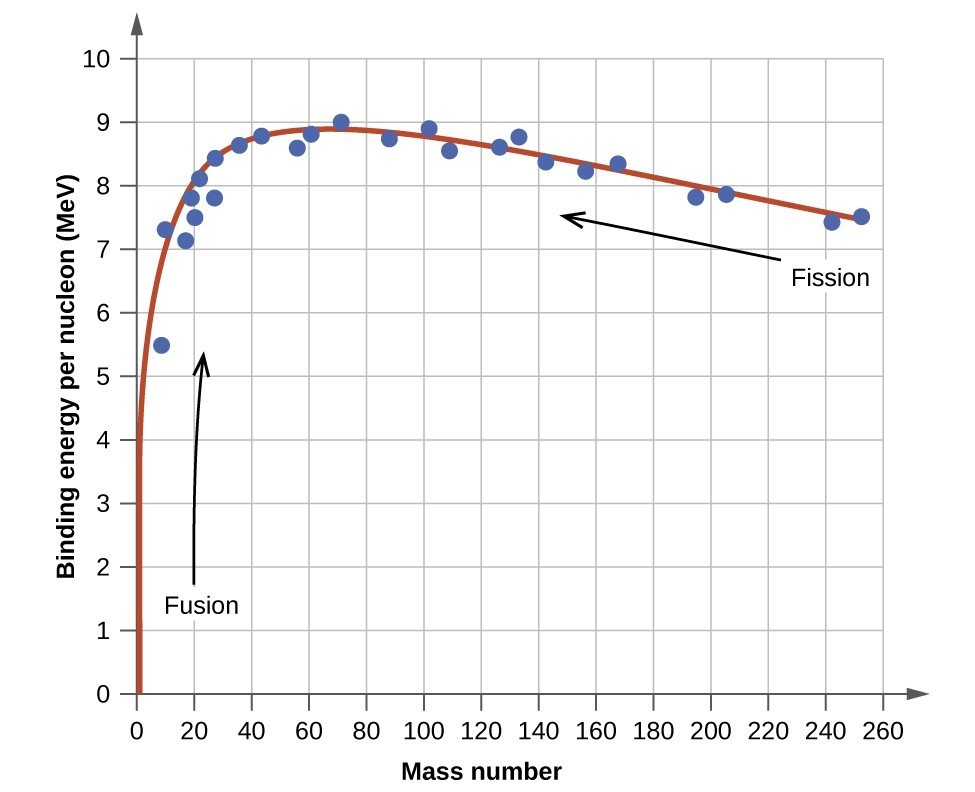
Misstatement of Stability: \ce{^{62}Ni} vs. \ce{^{56}Fe}
It is often (and incorrectly) stated that \ce{^{56}Fe} is the "most stable nucleus", but actually \ce{^{56}Fe} merely has the lowest mass per nucleon (not binding energy per nucleon) of all nuclides. The lower mass per nucleon in \ce{^{56}Fe} is enhanced by the fact that \ce{^{56}Fe} has 26/56 = 46.43% protons, while \ce{^{62}Ni} has only 28/62 = 45.16% protons, and the relatively larger fraction of light protons in \ce{^{56}Fe} lowers its average mass-per-nucleon ratio in a way that has no effect on its binding energy. \ce{^{56}Fe} is actually the third most stable nucleus (binding energy per nucleon) behind \ce{^{58}Fe} and \ce{^{62}Ni}.


