3.1: The Driving Mirror
- Page ID
- 7081
The mirror inside a car above the driver’s head and the outside mirror on the driver’s side are usually plane mirrors. The mirror I have in mind for this section, however, is the outside mirror on the passenger’s side. This is usually a convex mirror with some words inscribed on it that say something like “OBJECTS IN MIRROR ARE CLOSER THAN THEY APPEAR”.
The image formed by the convex mirror is actually an erect, diminished, virtual image, and it “appears” just a few inches behind the surface of the mirror. The object is much further away that it “appears” to be!
That, however, is not the main purpose of discussing this important scientific instrument. The reason that the outside mirror on the passenger side is convex is to give the driver a large field of view, so that this gives us an opportunity to think about the field of view of an optical system.
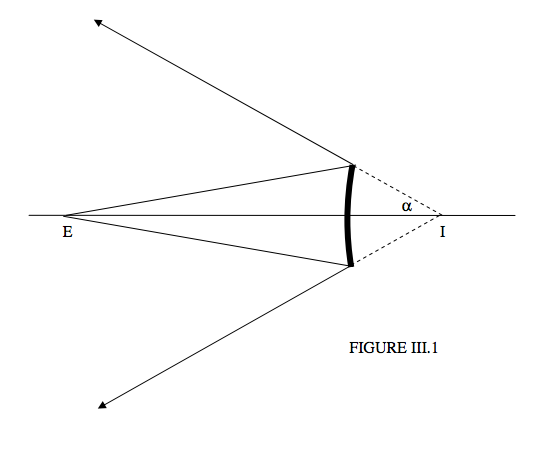
In Figure III.1, we see a convex mirror, and the observer’s eye is at E. (As with previous chapters, angles are supposed to be small, my artistic efforts notwithstanding.) The angle \(\alpha\) is evidently the radius of the field of view. How do we calculate it? Well, I hope it is clear from the drawing that the point I is actually the virtual image of the eye formed by the mirror. That being so, we can say:
The angular size of the field of view is equal to the angle subtended by the mirror at the image of the eye.
This is true of a concave mirror as well as of a convex or indeed a plane mirror, and is equally true when we look through a lens. (Draw the corresponding diagrams to convince yourself of this.)
Example \(\PageIndex{1}\)
Your eye is 50 cm in front of a convex mirror whose diameter is 4 cm and whose radius of curvature is 150 cm. What is the angular diameter of the field of view?
Solution
First we need to find the position of the image of the eye. Suppose it is at a distance \(q\) behind the mirror.
Final convergence = Initial convergence + power
The light is diverging before and after reflection, so both convergences are negative. The power of a mirror is \(−2n/r\), and here \(n = 1\) and \(r = +150\) cm, because the surface is convex. Thus
so the image is 30 cm behind the mirror. The diameter of the mirror is 4 cm, so that angular diameter of the mirror from I (i.e. the field of view) is 4/30 = 0.1333 rad = 7°38'.


