3.2: The Magnifying Glass

Two points about a magnifying glass to begin with. First, apparently rather few people understand how to use this complicated scientific instrument. The correct way to use it is to hold it as close to your eye as possible. The second point it that it doesn’t magnify at all. The angular size of the image is exactly the same as the angular size of the object.

Before examining the magnifying glass, it is probably useful to understand just a little about the workings of the human eye. I am not a biologist, I am very squeamish about any discussion of eyes, so I’ll keep this as basic as possible. When light enters the front surface or cornea of the eye, it is refracted in order to come to a focus on the back surface of the retina. The image on the retina is a real, inverted image, but the brain somehow corrects for that, so that objects look the right way up. While most of the refraction takes place at the cornea, some adjustment in the effective focal length is made possible by a flexible lens, whose power can be adjusted by means of ciliary muscles. The adjustment of this lens enables us to accommodate or bring to a focus objects that are at varying distances from us.

For an eye in good condition in a young person, the eye and the ciliary muscles are most relaxed when the eye is set to bring to a focus light from an infinitely-distant object – that is, when the eye is set to receive and bring to a focus light that is parallel before it enters the eye. In order to focus on a nearby object, the ciliary muscles have to make a bit of an effort to increase the power of the lens. They can increase the power of the lens only so far, however, and most people cannot focus on an object that is closer than a certain distance known as the near point. For young people the near point is usually taken to be 10 inches or 25 cm in calculations. The actual real point may differ from person to person; the figure of 25 cm is a “standard” near point. With older people, the near point recedes, so that 25 cm is too close for comfort, and the lens becomes less flexible.

When we use a magnifying glass properly (by holding it very close to the eye) we automatically place it so that the object we are looking at is at the focal point of the lens, and consequently parallel light emerges from the lens before it enters our eye. We don’t think about this. It is just that the ciliary muscles of the eye are most relaxed when they are set to bring to bring parallel light to a focus. It is merely the most comfortable thing to do. Figure III.2 shows a magnifying glass at work. As usual, angles are small and the lens is thin.

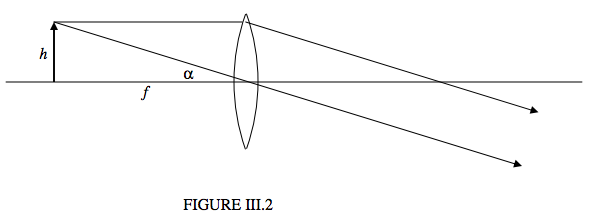
The object is in the focal plane of the lens. I draw two rays from the tip of the object. One is parallel to the axis, and, after passing through the lens, it passes through the focus on the other side of the lens. The other goes through the center of the lens. (Since the lens is thin, this ray is not laterally displaced.) Parallel rays emerge from the lens. The eye is immediately to the right of the lens, and it easily brings the parallel rays to a focus on the retina.

Although the lens does not actually produce an image, it is sometimes said that the lens produces “a virtual image at infinity”. The angular size of this virtual image is \(\alpha\), which is also the angular size of the object, namely \(\alpha = h/f\). Thus the angular size of the image is the same as the angular size of the object, and the lens hasn’t magnified at all!

However, if you put the object at a distance \(f\) (perhaps a few cm) from the eye without using the lens, you simply couldn’t focus your eye on it. Without the lens, the closest that you can put the object to your eye would be \(D\), the distance to the near point - 25 cm for a young eye. The angular size of the object would then be only \(h/D\).

The angular magnification of a magnifying glass is therefore defined as

\[\dfrac{\text{angular size of the image (which is}\space h/f )}{\text{angular size of the object when the object is at the near point (which is}\space h/D )}\]

Hence the magnification is equal to \(D/f\). The near point is taken to be 25 cm, so that a lens of focal length 2.5 cm has an angular magnification of 10.

If you bring the object just a little inside the focal plane, the light emerging on the other side will diverge, as it were from a virtual image that is no longer at infinity. (Figure III.3).

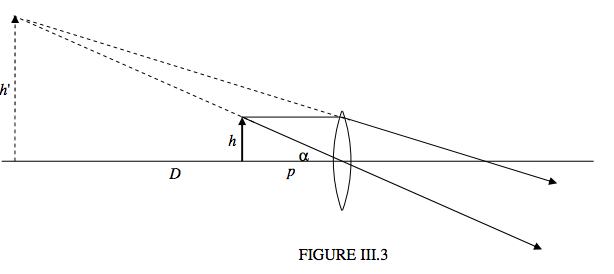
There is no point, however, in bringing the image closer than the near point. If you bring it to the near point, what must the object distance p be? A simple lens calculation shows that \(p = \frac{fD}{f+D}\). The angular size of the image is therefore \(\frac{h(f + D)}{fD}\). Since the angular size of the object when the object is at the near point is \(h/D\), the angular magnification is now \(\frac{D}{f}\) + 1 when the image is at the near point. This, for our \(f\) = 2.5 cm lens, the angular magnification is then 11.