3.4: The Camera

The camera is a box with a lens in one side of it and a photographic film or a CCD on the opposite side. The distance between camera lens and film can be changed so as to focus on objects at various distances. The aperture can also be changed. In dim light you need to open the aperture up to let a lot of light in; but this makes the image less sharp, and you have a smaller depth of field.

The aperture of a lens is merely its diameter, and it is usually expressed as a fraction of the focal length. Thus an aperture of \(f\)/22 is a small aperture. You can use this only in strong light, but you will then have nice sharp images and a large depth of field. An aperture of \(f\)/6.3 is wide open; the cone of light inside the camera is quite steep, and focussing is then quite critical. You use such a wide aperture only if you are forced to by dim light. The apertures typically available on a camera are often in steps with a ratio of approximately \(\sqrt{2}\) from one to the next. As you increase the aperture by a factor of \(\sqrt{2}\), you get twice as much light on the film (because this depends on the area of the exposed lens), so presumably you can cut the exposure time by one half. This is probably true for a CCD camera; the degree of blackening of a photographic film is not quite proportional to the product of the illuminance and the time, but at least it serves as a rough guide.

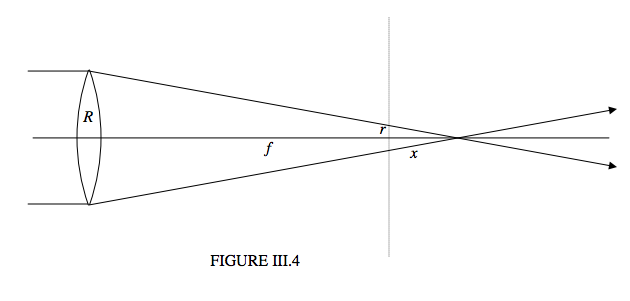
How is the depth of focus related to the aperture? Let us suppose that we have a lens that is free of aberrations such as spherical aberration, and that a point object produces a point image in the focal plane. If your film or CCD is not exactly in the plane, it will be illuminated not by a point image but by a small circle of finite diameter. If this circle is smaller than the grain or pixel size, you may wish to regard it as not seriously out of focus. So the question is: How far can you move the film away from the focal plane in either direction without the image being seriously out of focus? This range is the depth of focus.

In Figure III.4 we see a cone of light converging from a lens of radius \(R\) to a focal point at distance \(f\). Let us suppose that we place a film or CCD at the plane indicated by the dotted line at a distance \(x\) from the focal point, and that we are prepared to tolerate an out-of-focus “image” of radius \(r\). From similar triangles we see that \(x/r = f/R\). Or, if \(D\) is the diameter of the lens, and d is the diameter of the tolerable out-of-focus circle, \(x/d = f/D\). Thus we can place the film at a distance \(fd/D\) on either side of the true focal plane without appreciable degradation of the image. For example, if the aperture is \(D = f/6.3\), and you are prepared to tolerate an out-of-focus diameter \(d\) = 0.1 mm, the depth of focus will be ±6.3\(d\) or ±0.63 mm. On the other hand if you “stop down” to \(D = f/22\), your depth of focus will be 2.2 mm. Note that we have not been considering here the effect of spherical aberration, but of course this, too, increases with aperture, as well as merely the “out-of-focus” effect.

Notice that the tangent of the semi angle of the converging cone is \(R/f,\) or \(D/2f\). For apertures of \(f/6.3\) and \(f/22\), the semi angles are 4°.5 and 2°.6 respectively. This may give some comfort to those readers who have been uncomfortable with our assumption that angles are small. I have not been able to draw the lens and mirror drawings in these chapters with realistically small angles, because the drawings would be too cramped. I hope you will understand this shortcoming; you are welcome to try yourself!

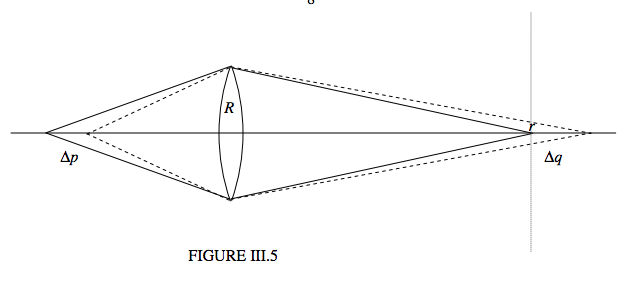
Depth of focus is not the same thing as depth of field. Suppose we want to photograph an object at a distance p from the camera lens, and that we are prepared to tolerate an out-offocus “image” of diameter up to \(d\), or radius \(r\). Any object at a distance within the range \(p \pm \Delta p\) may satisfy this, and we now want to find \(\Delta p\). Figure III.5 shows, with full lines, light from an object at distance \(p\) coming to a focus at a distance \(q\), and with dashed lines, light from an object at a distance \(\Delta p\) closer to the lens coming to a focus at a distance \(\Delta q\) further from the lens. The position of the film is indicated by the dotted line, and the radius of the out-of-focus dashed “image” is \(r\).

We have

\[ \frac{1}{q} = -\frac{1}{q} = -\frac{1}{p} + \frac{1}{f},\label{eq:3.5.1} \]

So that

\[ q = \frac{pf}{p-f}\label{eq:3.5.2} \]

and, without regard to sign

\[ \Delta q = - \left(\frac{f}{p-f}\right)^2 \Delta p. \label{eq:3.5.3} \]

From similar triangles we see that

\[\frac{R}{q+\Delta q }= \frac{r}{\Delta q}. \label{eq:3.5.4} \]

Elimination of \(q\) and \(\Delta q \) results in

\[ \Delta p = \frac{pr(p-f)}{f(R-r)}, \label{eq:3.5.5} \]

or, in terms of diameters rather than radii,

\[ \Delta p = \frac{pd(p-f)}{f(D-d)}.\label{eq:3.5.6} \]

For example, suppose the focal length is \(f = 25\) cm and you want to photograph an object at a distance of \(p\) = 400 cm. You are prepared to regard an out-of-focus “image” tolerable if its diameter is no larger than \(d\) = 0.1 mm. If the aperture is \(D = f/6.3\), you can photograph objects in the range (400 ± 15) cm, whereas if you “stop down” to \(D = f/22\), you can photograph objects in the range (400 ± 53) cm.

To the approximation that \(d << D\) and \(f << p\), Equation \(\ref{eq:3.5.6}\) becomes

\[\Delta p \approx \frac{p^2d}{fD}. \label{eq:3.5.7} \]