2.4: Electric and Magnetic Fields at a Boundary
- Page ID
- 7359
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
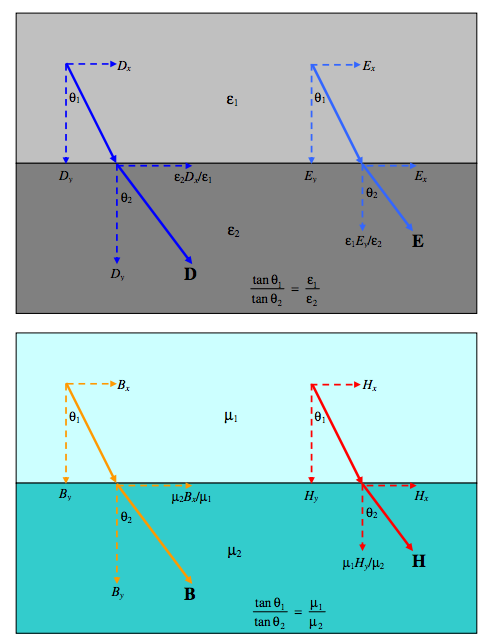
We next want to discuss the reflection and transmission for an arbitrary angle of incidence. Before we can do this it is well to remind ourselves (and this is just a reminder - we don’t go into the theory and definitions here) from electromagnetic theory how electric and magnetic fields behave at a boundary between two media.
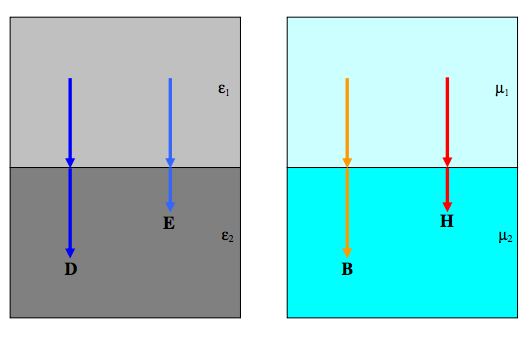
If an electric field is incident normally at the boundary between two media, \(E\) is larger in the medium with the smaller permittivity, whereas \(D\) is continuous. Likewise, if a magnetic field is incident normally at the boundary between two media, \(H\) is smaller in the medium with the higher permeability, whereas \(B\) is continuous.
That is:
\(D\)perp and \(B\)perp are continuous across a boundary.
\(E\)perp is inversely proportional to \( \epsilon\).
\(H\)perp is inversely proportional to \(\mu\).
See the drawing below.
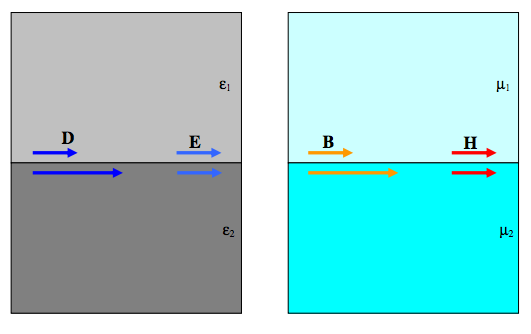
For fields parallel to a boundary, however, the situation is:
\(E\)tang and \(H\)tang are continuous across a boundary.
\(D\)tang is proportional to \(\epsilon\).
\(B\)tang is proportional to \(\mu\).
These things are assumed known from courses in electromagnetism. It may be asked what happens if a field is neither perpendicular to nor tangential to a boundary. We do not especially need to know that in discussing reflection of light at a boundary, because we shall be resolving any fields into their perpendicular and tangential components, but it is a reasonable question to ask, so for completeness the answers are given in the drawings below.