1.6: Refraction by a Prism
- Page ID
- 7071
Figure I.11 shows an isosceles prism of angle \(\alpha\) and a ray of light passing through it.
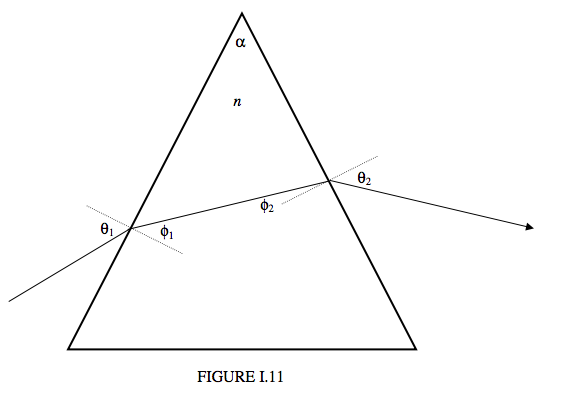
I have drawn just one ray of a single color. For white light, the colors will be dispersed, the violet light being deviated by the prism more than the red light. We’ll choose a wavelength such that the refractive index of the prism is \(n\). The deviation D of the light from its original direction is \(\theta_1 − \phi_1 + \theta_2 − \phi_2\). I want to imagine, now, if we keep the incident ray fixed and rotate the prism, how does the deviation vary with angle of incidence \(\theta_1\)? By geometry, \(\phi_2 = \alpha − \phi_1\), so that the deviation is
\[ D = \theta_1 + \theta_2 -\alpha.\label{eq:1.6.1} \]
Apply Snell’s law at each of the two refracting surfaces:
\[ \frac{\sin\theta_1}{\sin\phi_1} =n \quad \text{and} \quad \frac{\sin\theta_2}{\sin(\alpha - \phi_1)}=n, \label{eq:1.6.2a,b} \]
and eliminate \(\phi_1\):
\[ \sin\theta_2 = \sin\alpha\sqrt{n^2-\sin^2\theta_1} -\cos\alpha\sin\theta_1. \label{eq:1.6.3} \]
Equations \(\ref{eq:1.6.1}\) and \(\ref{eq:1.6.3}\) enable us to calculate the deviation as a function of the angle of incidence \(\theta_1\). The deviation is least when the light traverses the prism symmetrically, with \(\theta_1 = \theta_2\), the light inside the prism then being parallel to the base. Putting \(\theta_1 = \theta_2\) in equation shows that minimum deviation occurs for an angle of incidence given by
\[ \sin \theta _ { 1 } = \frac { n \sin \alpha } { \sqrt { 2 ( 1 + \cos \alpha ) } } = n \sin \frac { 1 } { 2 } \alpha. \label{eq:1.6.4} \]
The angle of minimum deviation \(D_{\text{min}}\) is \(2\theta_1 − \alpha\), where \(\theta_1\) is given by Equation \(\ref{eq:1.6.4}\), and this leads to the following relation between the refractive index and the angle of minimum deviation:
\[ n = \frac{\sin\frac{1}{2}(D_{\text{min}}+\alpha)}{\sin\frac{1}{2}\alpha}.\label{eq:1.6.5} \]
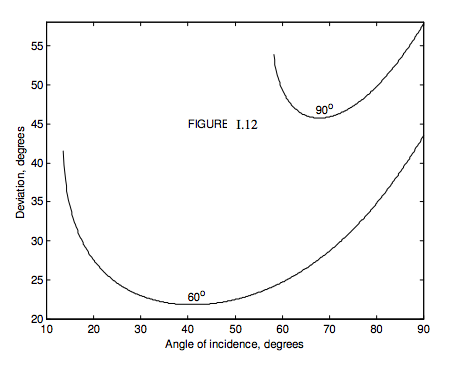
Of particular interest are prisms with \(\alpha\) = 60° and \(\alpha\) = 90°. I have drawn, in Figure I.12 the deviation versus angle of incidence for 60- and 90-degree prisms, using (for reasons I shall explain) \(n = 1.31\), which is approximately the refractive index of ice. For the 60° ice prism, the angle of minimum deviation is 21°.8, and for the 90° ice prism it is 45°.7.
Solar Halo
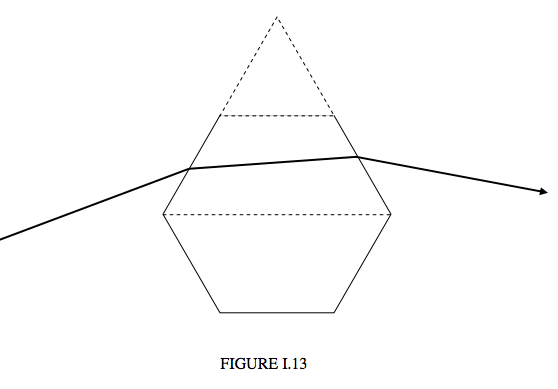
When hexagonal ice crystals are present in the atmosphere, sunlight is scattered in all directions, according to the angles of incidence on the various ice crystals (which may or may not be oriented randomly). However, the rate of change of the deviation with angle of incidence is least near minimum deviation; consequently much more light is deviated by 21°.8 than through other angles. Consequently we see a halo of radius about 22° around the Sun.
Seen sideways on, a hexagonal crystal is rectangular, and consequently refraction is as if through a 90° prism (Figure I.14):
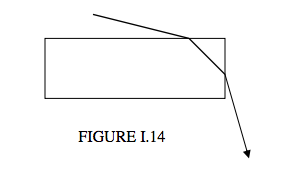
Again, the rate of change of deviation with angle of incidence is least near minimum deviation, and consequently we may see another halo, of radius about 46°. For both haloes, the violet is deviated more than the red, and therefore both haloes are tinged violet on the outside and red on the inside.
.jpg?revision=1)


