2.8B: Power of a Refracting Interface
- Page ID
- 9095
Figure II.12 shows a refracting interface of radius of curvature \(r\) separating media of indices \(n_1\) and \(n_2\).
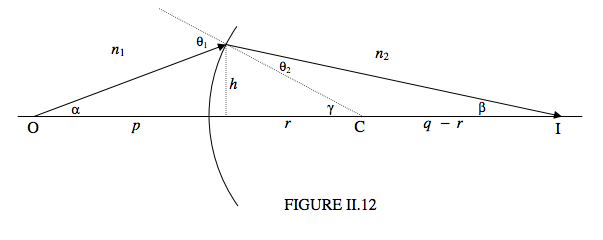
I show a real object at O, a real image at I and the centre of curvature at C. Remember that angles are small and the “lens” is thin. We see that \( h = \alpha p= \beta q = \gamma r\). By Euclid, \(\theta_1 = \alpha + \gamma\) and \(\theta_2 = \gamma - \beta \), and by Snell, \(n_1\theta_1 = n_2\theta_2\). From these we obtain
\[ \frac{n2}{q} = -\frac{n_1}{p} + \frac{n_2-n_1}{r}. \label{eq:2.8.3} \]
Thus the power is \(\frac{n_2-n_1}{r} \). The reader should try this for other situations (virtual object, virtual image, concave interface, and so on) to see that you always get the same result.


