6.5.1: Propagating Amplitudes
( \newcommand{\kernel}{\mathrm{null}\,}\)
We have seen that the amplitude for a given quantum state |ψ⟩ to later be found in another quantum state |ϕ⟩ is ⟨ϕ∣ψ⟩. Physically, when would you apply this amplitude? You would apply it when the system went through a device that measured whatever quantity |ϕ⟩ is associated with. For example, if you have an electron beam in state |ψ⟩ going into an SGz machine, you’d associate the amplitude ⟨+z∣ψ⟩ with the state |+z⟩ emerging from the positive output of the machine. What do you do, however, if the electron beam then goes through another machine? How do you deal with amplitudes when there is more than one process that might have a state change associated with it? The answer is that to get the overall amplitude for a starting state to end up in some final state, you multiply the individual amplitudes of each step the system went through.2
As an example, consider the following sequence of SG machines:
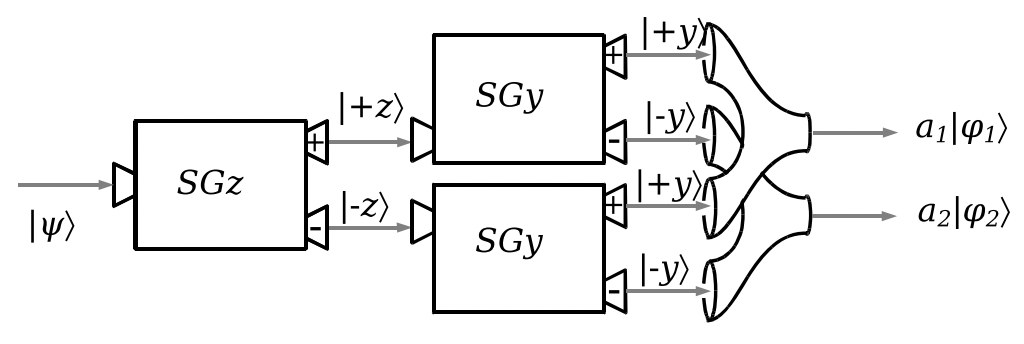
Yowza.3 An electron in some state |ψ⟩ goes into the beginning of this system. There are two possible places it may come out. It may emerge from the upper output in state |ϕ1⟩ (which is currently unknown, but we will figure it out); the amplitude for it to emerge here is a1. It may also emerge from the lower output in state |ϕ2⟩ (which we will also figure out); the amplitude for it to emerge from the lower output is a2.
Ultimately, what we’re interested in is the amplitude for the electron emerging from this whole thing with state |+y⟩, and the amplitude for it emerging with state |−y⟩. To figure those out, we need to trace the electron through all of the possible paths. At the input to the first machine, the electron is in the state |ψ⟩. At the positive output of the first machine, the electron is now either in the state |+z⟩, with amplitude ⟨+z∣ψ⟩, or in the state |−z⟩, with amplitude ⟨−z∣ψ⟩.
Let’s consider the possible paths for the electron if it comes out of the +z output of the first machine. If the electron goes this way, it will go into the upper SGy machine, with state |+z⟩. It will emerge from either the + output, with amplitude ⟨+y∣+z⟩, or from the − output, with amplitude ⟨−y∣+z⟩. The overall amplitude for the electron to make it from the very beginning to the + output of the upper second machine is the product of the amplitudes for each step: ⟨+z∣ψ⟩⟨+y∣+z⟩. Likewise, the overall amplitude for the electron to make it from the very beginning to the − output for the lower second machine is ⟨+z∣ψ⟩⟨+y∣+z⟩.
Next, consider the possible path of the electron emerging from the − output of the first machine. The amplitude for it to get this far is ⟨−z∣ψ⟩. The overall amplitude, then, for it to come out of the + output of the lower machine is ⟨−z∣ψ⟩⟨+y∣−z⟩, and the overall amplitude for it to come out of the − output of the lower machine is ⟨−z∣ψ⟩⟨−y∣−z⟩.
What do you do at a beam combiner? There, you just add the two states together, each multiplied by their respective amplitudes. Let’s first consider the upper beam combiner. The two states coming into this system, with their respective amplitudes, are:
⟨+z∣ψ⟩⟨+y∣+z⟩|+y⟩
and
⟨−z∣ψ⟩⟨+y∣−z⟩|+y⟩.
Therefore, the final output amplitude and state is:
a1|ϕ1⟩=[⟨+z∣ψ⟩⟨+y∣+z⟩+⟨−z∣ψ⟩⟨+y∣−z⟩]|+y⟩
By looking at this, we can see that the state |ϕ1⟩ is in fact just |+y⟩. Hopefully, that does not come as a surprise to you, as the state of the two electron beams going into this beam combiner was just |+y⟩. The amplitude a1 is then just
a1=⟨+z∣ψ⟩⟨+y∣+z⟩+⟨−z∣ψ⟩⟨+y∣−z⟩
The two state going into the lower beam combiner, with their respective amplitudes, are:
⟨+z∣ψ⟩⟨−y∣+z⟩|−y⟩
and
⟨−z∣ψ⟩⟨−y∣−z⟩|−y⟩.
Therefore, the final output amplitude and state for the lower output from this whole system is:
a2|ϕ2⟩=[⟨+z∣ψ⟩⟨−y∣+z⟩+⟨−z∣ψ⟩⟨−y∣−z⟩]|−y⟩
The state |ϕ2⟩, and the amplitude for the lower output is:
a2=⟨+z∣ψ⟩⟨−y∣+z⟩+⟨−z∣ψ⟩⟨−y∣−z⟩
As another example, consider the following collection of SG machines:
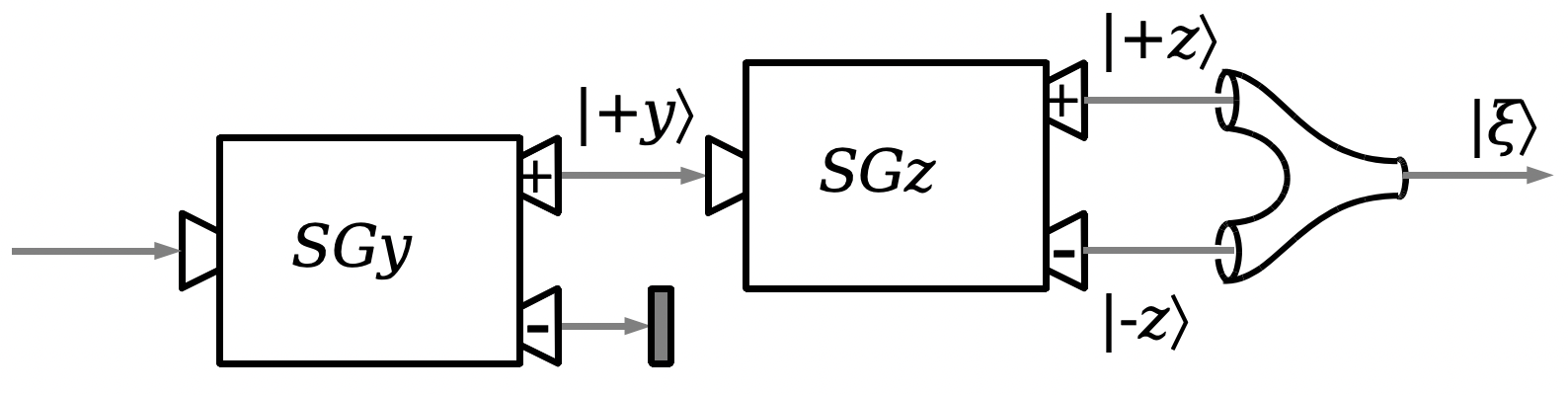
We know from the previous chapter that the final state of this system should be |+y⟩. Is that what we get?
In order to analyze this, you’re going to need to know how to express the states |+y⟩ and |−y⟩ in terms of |+z⟩ and |−z⟩:
|+y⟩=1√2|+z⟩+i√2|−z⟩|−y⟩=i√2|+z⟩+1√2|−z⟩
Consider the electron going into the input of the second machine. It is in state |+y⟩. We won’t worry about the amplitude for the initial electron to get into this state, because we’ll just consider the ones that happen to come out the positive output of the first machine. (The purpose of that first machine is to make sure that we know the electrons are in fact in the |+y⟩ state when they go into the second machine.) The amplitude for an electron to come out of the upper terminal is ⟨+z∣+y⟩, and the amplitude for an electron to come out of the lower terminal is ⟨−z∣+y⟩. Call the final state coming out of the beam combiner |ξ⟩. To figure out what this state is, combine together the two states going into it, each multiplied by their respective amplitudes:
|ξ⟩=⟨+z∣+y⟩|+z⟩+⟨−z∣+y⟩|−z⟩=⟨+z|(1√2|+z⟩+i√2|−z⟩)|+z⟩+⟨−z|(1√2|+z⟩+i√2|−z⟩)|−z⟩=(1√2⟨+z∣+z⟩+i√2⟨+z∣−z⟩)|+z⟩+(1√2⟨−z∣+z⟩+i√2⟨−z∣−z⟩)|−z⟩
Once again, we just have inner products of z states with themselves. We can use normalization (e.g. ⟨+z∣+z⟩=1) and orthogonality (e.g. ⟨−z∣+z⟩=0) to substitute in the numbers from the inner products in the expression above, yielding us:
|ξ⟩=(1√2(1)+i√2(0))|+z⟩+(1√2(0)+i√2(1))|−z⟩=1√2|+z⟩+i√2|−z⟩=|+y⟩
Sure enough, the mathematical rules for propagating amplitudes has given us the answer that we know is supposed to be right for the final state.
2This is different from classical physics, where you’d multiply the probabilities. You might wonder what the difference is, since you are going to square the whole thing at the end anyway. The differences comes from the fact that the quantum amplitudes may be complex, so the products of the individual amplitudes could end up with terms canceling each other.
3The reason why we have this complicated a collection of SG machines and beam combiners is that it’s important that we not be able to figure out which output from the SGz machine the electron went through, for subtle reasons that will be discussed in the next chapter.


