16.4: Solids

Roughly speaking, a solid is when a large collection of molecules are held together and fixed in place. They aren’t completely still, unless a solid is at absolute zero temperature. (And that’s not possible, as a result of Heisenberg’s Uncertainty Principle.) Most solids are at a higher temperature; the solids you interact with every day are approximately at room temperature, about 20^oC or 290 K. At such a temperature, the molecules are vibrating about, each with about 1/40 eV of kinetic energy in that vibration. Solids are held together different ways. Some solids form crystals, where every atom is bonded one way or another to neighboring atoms. Other solids do not strictly have covalent or ionic bonds holding everything together, but are held together by intermolecular forces resulting from the attraction of one electron cloud to a neighboring nucleus and the like.

In some particularly interesting solids, valence electrons don’t end up just being shared between neighboring atoms in molecules, but are rather associated with the solid as a whole. These solids may be conductors, if there are quantum states available for electrons to move about. When the valence electrons are associated with the solid as a whole, you can approximate the potential in which they move as as threedimensional square well the size of the solid. Of course, this isn’t exactly true, as there will be localized potential wells where each atom in the solid is. However, it is reasonable to approximate the solid as a fixed lattice, with valence electrons potentially free to move through it.

If you associate the valence electrons with the solid as a whole, you then need to think about the states available to those electrons. Since we are talking about a chunk of material that may have a huge number of atoms (e.g. about 10²² atoms if we’re talking a mere 1g sample of Copper), we’re also talking about a huge number of valence electrons, and a huge number of available states. Depending on how you model it, you can think of the states as resulting from the lattice, or as resulting from the effective square well potential in which the electrons move. The nature of the underlying lattice does matter. Typically, the states available to the valence electrons come in bands of energy, with gaps between the bands; this is one way in which a simple square well does not reflect the nature of the potential (where the distribution of states would be continuous). Three examples of solids with bands and band gaps are shown below. Each diagram is an energy level diagram. In a shaded band, there are many electron states stacked one on top of the other. Because electrons are fermions, however, each individual state may only have two electrons (two, not one, because of electron spin).

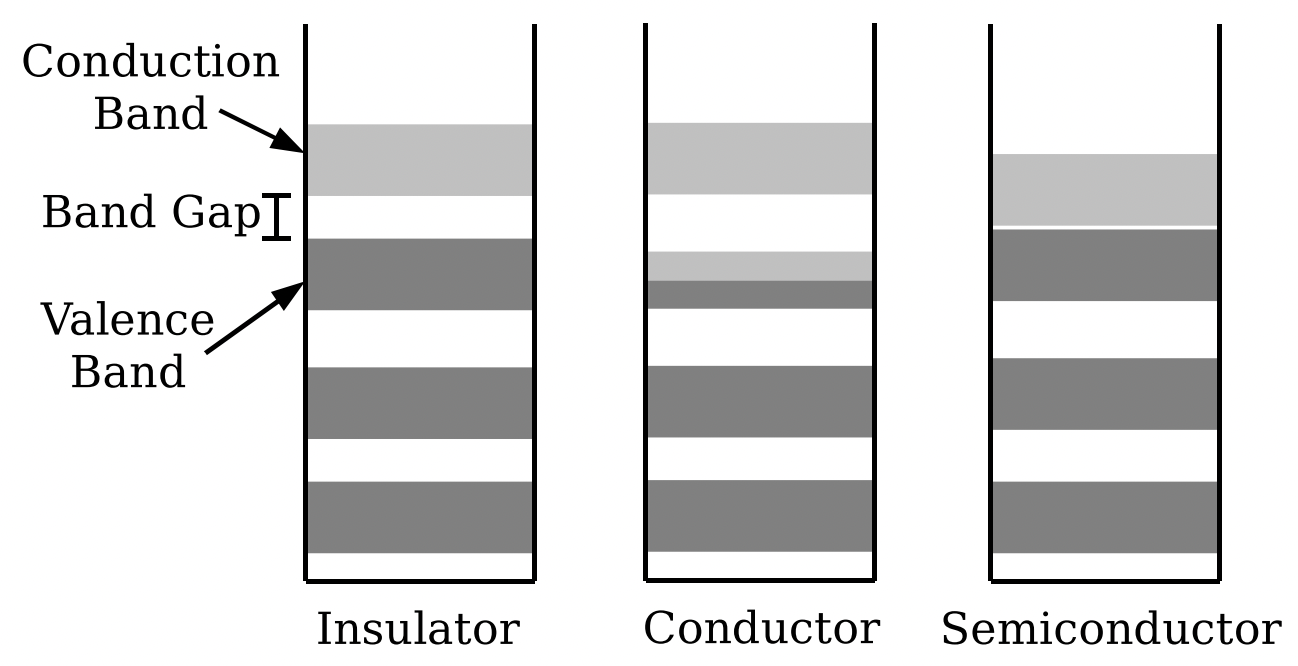Electron energy states in the band gap model of solids. Increasing energy is upwards on all three diagrams. Dark gray bands indicate bands of many energy states that are filled. Light Gray bands indicate bands of many empty energy states.

In the figure on the left, the top filled band is called the valence band. Again, this band, and the band below it, represent a huge number of closely spaced energy states for valence electrons. The energy of the top filled state (assuming the solid as a whole is in its lowest overall energy state) is called the Fermi energy. These states are not places where the electron can be, in the sense of places in space. Electrons in higher states have more energy than electrons in lower states, so they are in fact moving around. However, they’re not moving around in a way that would allow electrons to flow in a coordinated fashion from one side of the solid to another. Rather, they’re moving around in the same way that an electron in a higher orbital of an atom that has some kinetic energy associated with it. The electron is still tied to the solid, and stuck in the energy state it’s in. But, that state is not localized to one nucleus; it’s associated with the insulator as a whole. That there are no empty states nearby is why nothing can change that would allow for electric conduction.

The first empty band above the filled band is the conduction band. If you want to conduct electricity— that is, allow charge to move through the solid— you need to be able to get electrons out of the states where they’re fixed, and into states that have empty states nearby. If there is a band gap between the valence band and the conduction band, this is not very easy; it takes a lot of energy to get an electron out of the state where it normally is and into a state where there are many neighboring states, allowing it to move in a coordinated way through the solid. The conduction band is the band where there are lots of empty states that the electron can make transitions between (or occupy in a superposition of states) so as to allow it to move through the solid and thereby carry electric current. (Electric current ultimately is just the transfer of net electron charge from one side of the conductor to the other.) Every material will ultimately carry electron current, if you apply enough potential to it. However, the wider the band gap, the more energy it takes to liberate an electron from the valence band and into the conduction band, thereby allowing it to move freely. If there is a wide gap, we would consider the material an insulator.

In the middle figure above, the material is a conductor. Here, the Fermi energy is in the middle of a band of available energy states. As such, electrons in the top filled states have many nearby states available to them. They may freely change states, and thus are able to go into states that can correspond to electrons transferring charge through the material.

The rightmost figure above is a semiconductor. Here, there is a band gap between the valence and conduction bands, but that band gap is quite small. Because of thermal excitations— electrons bumped about by the vibrating atoms resulting from the non-zero temperature— a tiny fraction of the electrons will in fact be up in the conduction band. However, the conductivity of this material remains small, because not very many electrons are up there. (The conductivity will go up with temperature, however, as more electrons statistically get bumped up into the conduction band.) The typical band gap in a semiconductor is around 1–2 eV, which is a lot larger than the 1/40 eV that is the average energy available to one particle at room temperature. By doping a semiconductor— that is, adding impurities— you can either add additional valence electrons inside the band gap at an energy just below the conduction band, or additional valence states at an energy inside the band gap just above the valence band. By putting such doped semiconductors together, you can create devices with interesting electrical properties, such as diodes and transistors.

One thing that is interesting about solids is what happens when you try to compress the solid. In a square well, if you decrease the width of the well the energy of all the states increases:

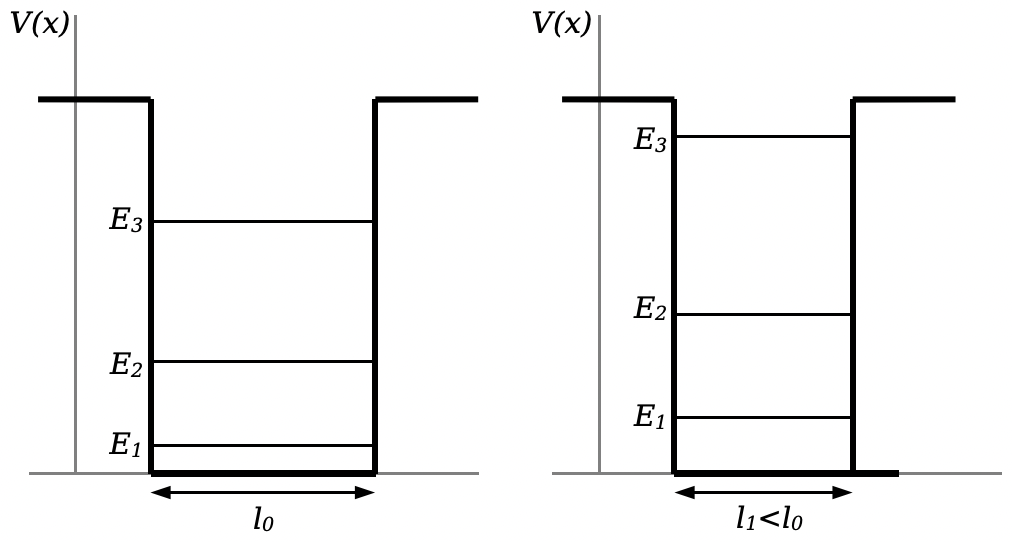
If you think about squeezing a solid, what this means is that you’re pushing the states occupied by the valence electrons to higher energy levels, and therefore you must be putting energy into the solid. The need to exert energy on a solid when squeezing will manifest as a pressure (force per area) that resists the force trying to squeeze the solid. While you might think that it is the atoms and molecules themselves resisting being pushed closer together that makes a solid resist being compressed, this is not the whole case. In fact, this additional energy put into the valence electrons— which, remember, are not associated with individual electrons, but with the solid as a whole— contributes significantly to the restorative pressure of a compressed solid. This pressure is called Fermi degeneracy pressure. In this circumstance, “degeneracy” is a technical term referring to electrons all being packed into states as tightly as they can. The Fermi degeneracy pressure that resists the compression of a solid is a direct result of those states rising to higher energies as a result of the compression.