2.10: Wave-Packets
- Page ID
- 16025
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The previous discussion suggests that the wavefunction of a massive particle of momentum \(p\) and energy \(E\), moving in the positive \(x\)-direction, can be written \[\label{e2.41} \psi(x,t) = \bar{\psi}\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)},\] where \(k= p/\hbar>0\) and \(\omega = E/\hbar>0\). Here, \(\omega\) and \(k\) are linked via the dispersion relation ([e2.38]). Expression ([e2.41]) represents a plane-wave whose maxima and minima propagate in the positive \(x\)-direction with the phase-velocity \(v_p=\omega/k\). As we have seen, this phase-velocity is only half of the classical velocity of a massive particle.
From before, the most reasonable physical interpretation of the wavefunction is that \(|\psi(x,t)|^{\,2}\) is proportional to the probability density of finding the particle at position \(x\) at time \(t\). However, the modulus squared of the wavefunction ([e2.41]) is \(|\bar{\psi}|^{\,2}\), which depends on neither \(x\) nor \(t\). In other words, this wavefunction represents a particle that is equally likely to be found anywhere on the \(x\)-axis at all times. Hence, the fact that the maxima and minima of the wavefunction propagate at a phase-velocity that does not correspond to the classical particle velocity does not have any real physical consequences.
How can we write the wavefunction of a particle that is localized in \(x\): that is, a particle that is more likely to be found at some positions on the \(x\)-axis than at others? It turns out that we can achieve this goal by forming a linear combination of plane-waves of different wavenumbers: in other words, \[\label{e2.42} \psi(x,t) = \int_{-\infty}^{\infty} \bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,(k\,x-\omega\,t)}\,dk.\] Here, \(\bar{\psi}(k)\) represents the complex amplitude of plane-waves of wavenumber \(k\) in this combination. In writing the previous expression, we are relying on the assumption that particle waves are superposable: that is, that it is always possible to add two valid wave solutions to form a third valid wave solution. The ultimate justification for this assumption is that particle waves satisfy a differential wave equation that is linear in \(\psi\). As we shall see, in Section 1.15, this is indeed the case. Incidentally, a plane-wave that varies as \(\exp[\,{\rm i}\,(k\,x-\omega\,t)]\) and has a negative \(k\) (but positive \(\omega\)) propagates in the negative \(x\)-direction at the phase-velocity \(\omega/|k|\). Hence, the superposition ([e2.42]) includes both forward and backward propagating waves.
There is a useful mathematical theorem, known as Fourier’s theorem , which states that if \[\label{e2.43} f(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \bar{f}(k)\,{\rm e}^{\,{\rm i}\,k\,x}\,dk,\] then \[\label{e2.44} \bar{f}(k) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty f(x)\,{\rm e}^{-{\rm i}\,k\,x}\,dx.\] Here, \(\bar{f}(k)\) is known as the Fourier transform of the function \(f(x)\). We can use Fourier’s theorem to find the \(k\)-space function \(\bar{\psi}(k)\) that generates any given \(x\)-space wavefunction \(\psi(x)\) at a given time.
For instance, suppose that at \(t=0\) the wavefunction of our particle takes the form \[\label{e2.45} \psi(x,0) \propto \exp\left[{\rm i}\,k_0\,x - \frac{(x-x_0)^{\,2}}{4\,({\mit\Delta}x)^{\,2}}\right].\] Thus, the initial probability density of the particle is written \[\label{e2.46} |\psi(x,0)|^{\,2} \propto \exp\left[- \frac{(x-x_0)^{\,2}}{2\,({\mit\Delta}x)^{\,2}}\right].\] This particular probability distribution is called a Gaussian distribution, and is plotted in Figure [f4]. It can be seen that a measurement of the particle’s position is most likely to yield the value \(x_0\), and very unlikely to yield a value which differs from \(x_0\) by more than \(3\,{\mit\Delta} x\). Thus, Equation ([e2.45]) is the wavefunction of a particle that is initially localized around \(x=x_0\) in some region whose width is of order \({\mit\Delta} x\). This type of wavefunction is known as a wave-packet.
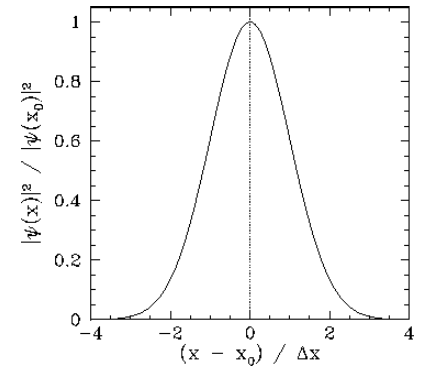
Figure 7: A Gaussian probability distribution in ![]() -space.
-space.
According to Equation ([e2.42]), \[\psi(x,0) = \int_{-\infty}^{\infty} \bar{\psi}(k)\,{\rm e}^{\,{\rm i}\,k\,x}\,dk.\] Hence, we can employ Fourier’s theorem to invert this expression to give \[\label{e2.42a} \bar{\psi}(k)\propto \int_{-\infty}^{\infty} \psi(x,0)\,{\rm e}^{-{\rm i}\,k\,x}\,dx.\] Making use of Equation ([e2.45]), we obtain \[\bar{\psi}(k) \propto {\rm e}^{-{\rm i}\,(k-k_0)\,x_0}\int_{-\infty}^{\infty} \exp\left[ -{\rm i}\,(k-k_0)\,(x-x_0) - \frac{(x-x_0)^{\,2}}{4\,({\mit\Delta}x)^{\,2}}\right]dx.\] Changing the variable of integration to \(y=(x-x_0)/ (2\,{\mit\Delta} x)\), this reduces to \[\bar{\psi}(k) \propto {\rm e}^{-{\rm i}\,k\,x_0} \int_{-\infty}^{\infty}\exp\left(-{\rm i}\,\beta\,y - y^{\,2}\right) dy,\] where \(\beta = 2\,(k-k_0)\,{\mit\Delta}x\). The previous equation can be rearranged to give \[\bar{\psi}(k) \propto {\rm e}^{-{\rm i}\,k\,x_0 - \beta^{\,2}/4}\int_{-\infty}^{\infty} {\rm e}^{-(y-y_0)^{\,2}}\,dy,\] where \(y_0 = - {\rm i}\,\beta/2\). The integral now just reduces to a number, as can easily be seen by making the change of variable \(z=y-y_0\). Hence, we obtain \[\label{e2.51} \bar{\psi}(k) \propto \exp\left[-{\rm i}\,k\,x_0 - \frac{(k-k_0)^{\,2}}{4\,({\mit\Delta}k)^{\,2}}\right],\] where \[{\mit\Delta} k = \frac{1}{2\,{\mit\Delta} x}.\]
If \(|\psi(x)|^{\,2}\) is proportional to the probability density of a measurement of the particle’s position yielding the value \(x\) then it stands to reason that \(|\bar{\psi}(k)|^{\,2}\) is proportional to the probability density of a measurement of the particle’s wavenumber yielding the value \(k\). (Recall that \(p = \hbar\,k\), so a measurement of the particle’s wavenumber, \(k\), is equivalent to a measurement of the particle’s momentum, \(p\)). According to Equation ([e2.51]), \[\label{e2.53} |\bar{\psi}(k)|^{\,2} \propto \exp\left[- \frac{(k-k_0)^{\,2}}{2\,({\mit\Delta}k)^{\,2}}\right].\] Note that this probability distribution is a Gaussian in \(k\)-space. [See Equation ([e2.46]) and Figure [f4].] Hence, a measurement of \(k\) is most likely to yield the value \(k_0\), and very unlikely to yield a value which differs from \(k_0\) by more than \(3\,{\mit\Delta}k\). Incidentally, a Gaussian is the only simple mathematical function in \(x\)-space that has the same form as its Fourier transform in \(k\)-space.
We have just seen that a Gaussian probability distribution of characteristic width \({\mit\Delta} x\) in \(x\)-space [see Equation ([e2.46])] transforms to a Gaussian probability distribution of characteristic width \({\mit\Delta} k\) in \(k\)-space [see Equation ([e2.53])], where \[{\mit\Delta}x\,{\mit\Delta} k = \frac{1}{2}.\] This illustrates an important property of wave-packets. Namely, if we wish to construct a packet that is very localized in \(x\)-space (i.e., if \({\mit\Delta}x\) is small) then we need to combine plane-waves with a very wide range of different \(k\)-values (i.e., \({\mit\Delta}k\) will be large). Conversely, if we only combine plane-waves whose wavenumbers differ by a small amount (i.e., if \({\mit\Delta}k\) is small) then the resulting wave-packet will be very extended in \(x\)-space (i.e., \({\mit\Delta}x\) will be large).
Contributors and Attributions
Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)
\( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)

