According to special relativity, the kinetic energy (i.e., the difference between the total energy and the rest mass energy) of a particle of rest mass m and momentum p is T=√p2c2+m2c4−mc2.
In the non-relativistic limit p≪mc, we can expand the square-root in the previous expression to give T=p22m[1−14(pmc)2+O(pmc)4].
Hence, T≃p22m−p48m3c2.
Of course, we recognize the first term on the right-hand side of this equation as the standard non-relativistic expression for the kinetic energy. The second term is the lowest-order relativistic correction to this energy. Let us consider the effect of this type of correction on the energy levels of a hydrogen atom. So, the unperturbed Hamiltonian is given by Equation ([e12.58]), and the perturbing Hamiltonian takes the form H1=−p48m3ec2.
Now, according to standard first-order perturbation theory (see Section 1.4), the lowest-order relativistic correction to the energy of a hydrogen atom state characterized by the standard quantum numbers n, l, and m is given by ΔEnlm=⟨n,l,m|H1|n,l,m⟩=−18m3ec2⟨n,l,m|p4|n,l,m⟩=−18m3ec2⟨n,l,m|p2p2|n,l,m⟩.
However, Schrödinger’s equation for a unperturbed hydrogen atom can be written p2ψn,l,m=2me(En−V)ψn,l,m,
where V=−e2/(4πϵ0r). Because p2 is an Hermitian operator, it follows that ΔEnlm=−12mec2⟨n,l,m|(En−V)2|n,l,m⟩=−12mec2(E2n−2En⟨n,l,m|V|n,l,m⟩+⟨n,l,m|V2|n,l,m⟩)=−12mec2[E2n+2En(e24πϵ0)⟨1r⟩+(e24πϵ0)2⟨1r2⟩].
It follows from Equations ([e9.74]) and ([e9.75]) that ΔEnlm=−12mec2[E2n+2En(e24πϵ0)1n2a0+(e24πϵ0)21(l+1/2)n3a20].
Finally, making use of Equations ([e9.55]), ([e9.56]), and ([e9.57]), the previous expression reduces to
ΔEnlm=Enα2n2(nl+1/2−34),
where α=e24πϵ0ℏc≃1137
is the dimensionless fine structure constant.
Note that the previous derivation implicitly assumes that p4 is an Hermitian operator. It turns out that this is not the case for l=0 states. However, somewhat fortuitously, our calculation still gives the correct answer when l=0. Note, also, that we are able to employ non-degenerate perturbation theory in the previous calculation, using the ψnlm eigenstates, because the perturbing Hamiltonian commutes with both L2 and Lz. It follows that there is no coupling between states with different l and m quantum numbers. Hence, all coupled states have different n quantum numbers, and therefore have different energies.
Now, an electron in a hydrogen atom experiences an electric field E=er4πϵ0r3
due to the charge on the nucleus. However, according to electromagnetic theory, a non-relativistic particle moving in a electric field E with velocity v also experiences an effective magnetic field
B=−v×Ec2
Recall, that an electron possesses a magnetic moment [see Equations ([e10.58]) and ([e10.59])] μ=−emeS
due to its spin angular momentum, S. We, therefore, expect an additional contribution to the Hamiltonian of a hydrogen atom of the form [see Equation ([e10.60a])] H1=−μ⋅B=−e24πϵ0mec2r3v×r⋅S=e24πϵ0m2ec2r3L⋅S,
where L=mer×v is the electron’s orbital angular momentum. This effect is known as spin-orbit coupling. It turns out that the previous expression is too large, by a factor 2, due to an obscure relativistic effect known as Thomas precession . Hence, the true spin-orbit correction to the Hamiltonian is
H1=e28πϵ0m2ec2r3L⋅S.
Let us now apply perturbation theory to the hydrogen atom, using the previous expression as the perturbing Hamiltonian.
Now, J=L+S
is the total angular momentum of the system. Hence, J2=L2+S2+2L⋅S,
giving L⋅S=12(J2−L2−S2).
Recall, from Section [s11.2], that while J2 commutes with both L2 and S2, it does not commute with either Lz or Sz. It follows that the perturbing Hamiltonian ([e12.127]) also commutes with both L2 and S2, but does not commute with either Lz or Sz. Hence, the simultaneous eigenstates of the unperturbed Hamiltonian ([e12.58]) and the perturbing Hamiltonian ([e12.127]) are the same as the simultaneous eigenstates of L2, S2, and J2 discussed in Section [s11.3]. It is important to know this because, according to Section 1.6, we can only safely apply perturbation theory to the simultaneous eigenstates of the unperturbed and perturbing Hamiltonians.
Adopting the notation introduced in Section [s11.3], let ψ(2)l,s;j,mj be a simultaneous eigenstate of L2, S2, J2, and Jz corresponding to the eigenvalues L2ψ(2)l,s;j,mj=l(l+1)ℏ2ψ(2)l,s;j,mj,S2ψ(2)l,s;j,mj=s(s+1)ℏ2ψ(2)l,s;j,mj,J2ψ(2)l,s;j,mj=j(j+1)ℏ2ψ(2)l,s;j,mj,Jzψ(2)l,s;j,mj=mjℏψ(2)l,s;j,mj.
According to standard first-order perturbation theory, the energy-shift induced in such a state by spin-orbit coupling is given by ΔEl,1/2;j,mj=⟨l,1/2;j,mj|H1|l,1/2;j,mj⟩=e216πϵ0m2ec2⟨1,1/2;j,mj|J2−L2−S2r3|l,1/2;j,mj⟩=e2ℏ216πϵ0m2ec2[j(j+1)−l(l+1)−3/4]⟨1r3⟩.
Here, we have made use of the fact that s=1/2 for an electron. It follows from Equation ([e9.75a]) that ΔEl,1/2;j,mj=e2ℏ216πϵ0m2ec2a30[j(j+1)−l(l+1)−3/4l(l+1/2)(l+1)n3],
where n is the radial quantum number. Finally, making use of Equations ([e9.55]), ([e9.56]), and ([e9.57]), the previous expression reduces to
ΔEl,1/2;j,mj=Enα2n2[n{3/4+l(l+1)−j(j+1)}2l(l+1/2)(l+1)],
where α is the fine structure constant. A comparison of this expression with Equation ([e12.121]) reveals that the energy-shift due to spin-orbit coupling is of the same order of magnitude as that due to the lowest-order relativistic correction to the Hamiltonian. We can add these two corrections together (making use of the fact that j=l±1/2 for a hydrogen atom—see Section [s11.3]) to obtain a net energy-shift of
ΔEl,1/2;j,mj=Enα2n2(nj+1/2−34).
This modification of the energy levels of a hydrogen atom due to a combination of relativity and spin-orbit coupling is known as fine structure.
Now, it is conventional to refer to the energy eigenstates of a hydrogen atom that are also simultaneous eigenstates of J2 as nLj states, where n is the radial quantum number, L=(S,P,D,F,⋯) as l=(0,1,2,3,⋯), and j is the total angular momentum quantum number. Let us examine the effect of the fine structure energy-shift ([e12.138]) on these eigenstates for n=1,2 and 3.
For n=1, in the absence of fine structure, there are two degenerate 1S1/2 states. According to Equation ([e12.138]), the fine structure induced energy-shifts of these two states are the same. Hence, fine structure does not break the degeneracy of the two 1S1/2 states of hydrogen.
For n=2, in the absence of fine structure, there are two 2S1/2 states, two 2P1/2 states, and four 2P3/2 states, all of which are degenerate. According to Equation ([e12.138]), the fine structure induced energy-shifts of the 2S1/2 and 2P1/2 states are the same as one another, but are different from the induced energy-shift of the 2P3/2 states. Hence, fine structure does not break the degeneracy of the 2S1/2 and 2P1/2 states of hydrogen, but does break the degeneracy of these states relative to the 2P3/2 states.
For n=3, in the absence of fine structure, there are two 3S1/2 states, two 3P1/2 states, four 3P3/2 states, four 3D3/2 states, and six 3D5/2 states, all of which are degenerate. According to Equation ([e12.138]), fine structure breaks these states into three groups: the 3S1/2 and 3P1/2 states, the 3P3/2 and 3D3/2 states, and the 3D5/2 states.
The effect of the fine structure energy-shift on the n=1, 2, and 3 energy states of a hydrogen atom is illustrated in Figure below:
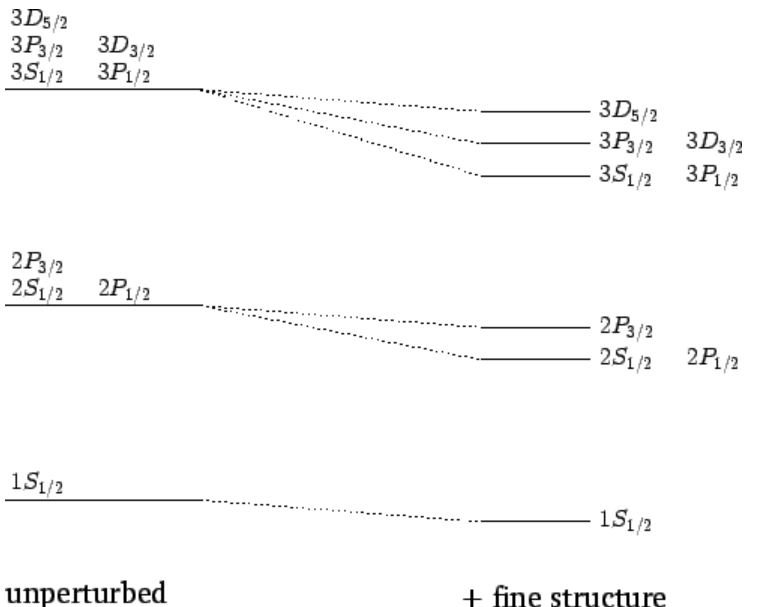
Figure 23: Effect of the fine structure energy-shift on the  and 3 states of a hydrogen atom. Not to scale.
and 3 states of a hydrogen atom. Not to scale.
Note, finally, that although expression ([e12.137]) does not have a well defined value for l=0, when added to expression ([e12.121]) it, somewhat fortuitously, gives rise to an expression ([e12.138]) that is both well-defined and correct when l=0.
Contributors and Attributions

![]() and 3 states of a hydrogen atom. Not to scale.
and 3 states of a hydrogen atom. Not to scale.

