11.9: Zeeman Effect

Consider a hydrogen atom placed in a uniform \(z\)-directed external magnetic field of magnitude \(|{\bf B}|\). The modification to the Hamiltonian of the system is \[H_1 = -\mu\cdot{\bf B},\] where \[\mu = - \frac{e}{2\,m_e}\,({\bf L} + 2\,{\bf S})\] is the total electron magnetic moment, including both orbital and spin contributions. [See Equations ([e10.57])–([e10.59]).] Thus, \[H_1 = \frac{e\,B}{2\,m_e}\,(L_z+ 2\,S_z).\]

Suppose that the applied magnetic field is much weaker than the atom’s internal magnetic field, ([e12.124]). Because the magnitude of the internal field is about 25 tesla, this is a fairly reasonable assumption. In this situation, we can treat \(H_1\) as a small perturbation acting on the simultaneous eigenstates of the unperturbed Hamiltonian and the fine structure Hamiltonian. Of course, these states are the simultaneous eigenstates of \(L^2\), \(S^2\), \(J^{\,2}\), and \(J_z\). (See the previous section.) Hence, from standard perturbation theory, the first-order energy-shift induced by a weak external magnetic field is \[\begin{aligned} {\mit\Delta} E_{l,1/2;j,m_j} &= \langle l,1/2;j,m_j|H_1|l,1/2;j,m_j\rangle\nonumber\\[0.5ex] &= \frac{e\,B}{2\,m_e}\,\left(m_j\,\hbar + \langle l,1/2;j,m_j|S_z|l,1/2;j,m_j\rangle\right),\end{aligned}\] because \(J_z=L_z+S_z\). Now, according to Equations ([e11.47]) and ([e11.48]),

\[\label{e12.143} \psi^{(2)}_{j,m_j} = \left(\frac{j+m_j}{2\,l+1}\right)^{1/2}\psi^{(1)}_{m_j-1/2,1/2} + \left(\frac{j-m_j}{2\,l+1}\right)^{1/2}\,\psi^{(1)}_{m_j+1/2,-1/2}\] when \(j=l+1/2\), and \[\psi^{(2)}_{j,m_j} = \left(\frac{j+1-m_j}{2\,l+1}\right)^{1/2}\psi^{(1)}_{m_j-1/2,1/2} - \left(\frac{j+1+m_j}{2\,l+1}\right)^{1/2}\,\psi^{(1)}_{m_j+1/2,-1/2}\] when \(j=l-1/2\). Here, the \(\psi^{(1)}_{m,m_s}\) are the simultaneous eigenstates of \(L^2\), \(S^2\), \(L_z\), and \(S_z\), whereas the \(\psi^{(2)}_{j,m_j}\) are the simultaneous eigenstates of \(L^2\), \(S^2\), \(J^{\,2}\), and \(J_z\). In particular, \[\label{e12.145} S_z\,\psi^{(1)}_{m,\pm 1/2} = \pm \frac{\hbar}{2}\,\psi^{(1)}_{m,\pm 1/2}.\] It follows from Equations ([e12.143])–([e12.145]), and the orthormality of the \(\psi^{(1)}\), that \[\langle l,1/2;j,m_j|S_z|l,1/2;j,m_j\rangle = \pm \frac{m_j\,\hbar}{2\,l+1}\] when \(j=l\pm 1/2\). Thus, the induced energy-shift when a hydrogen atom is placed in an external magnetic field—which is known as the Zeeman effect —becomes \[\label{e12.147} {\mit\Delta} E_{l,1/2;j,m_j} = \mu_B\,B\,m_j\left(1\pm \frac{1}{2\,l+1}\right)\] where the \(\pm\) signs correspond to \(j=l\pm 1/2\). Here, \[\mu_B = \frac{e\,\hbar}{2\,m_e} = 5.788\times 10^{-5}\,{\rm eV/T}\] is known as the Bohr magnetron. Of course, the quantum number \(m_j\) takes values differing by unity in the range \(-j\) to \(j\). It, thus, follows from Equation ([e12.147]) that the Zeeman effect splits degenerate states characterized by \(j=l+1/2\) into \(2\,j+1\) equally spaced states of interstate spacing \[\label{e12.149} {\mit\Delta} E_{j=l+1/2} = \mu_B\,B\left(\frac{2\,l+2}{2\,l+1}\right).\] Likewise, the Zeeman effect splits degenerate states characterized by \(j=l-1/2\) into \(2\,j+1\) equally spaced states of interstate spacing \[\label{e12.150} {\mit\Delta} E_{j=l-1/2} = \mu_B\,B\left(\frac{2\,l}{2\,l+1}\right).\]

In conclusion, in the presence of a weak external magnetic field, the two degenerate \(1S_{1/2}\) states of the hydrogen atom are split by \(2\,\mu_B\,B\). Likewise, the four degenerate \(2S_{1/2}\) and \(2P_{1/2}\) states are split by \((2/3)\,\mu_B\,B\), whereas the four degenerate \(2P_{3/2}\) states are split by \((4/3)\,\mu_B\,B\). This is illustrated in Figure [fzee]. Note, finally, that because the \(\psi^{(2)}_{l,m_j}\) are not simultaneous eigenstates of the unperturbed and perturbing Hamiltonians, Equations ([e12.149]) and ([e12.150]) can only be regarded as the expectation values of the magnetic-field induced energy-shifts. However, as long as the external magnetic field is much weaker than the internal magnetic field, these expectation values are almost identical to the actual measured values of the energy-shifts.

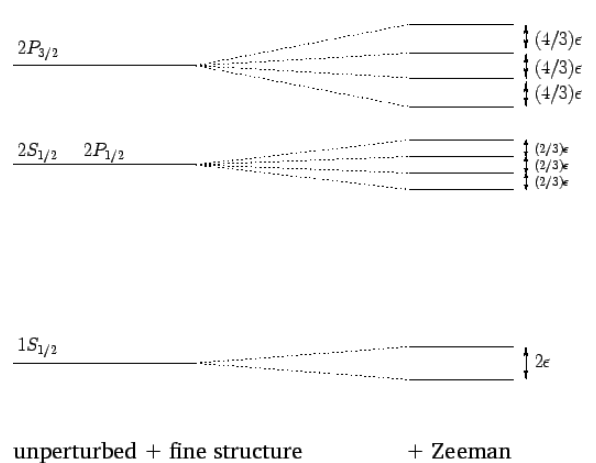
Figure 24: The Zeeman effect for the and states of a hydrogen atom. Here, \(\begin{equation}\epsilon=\mu_{B} B\end{equation}\). Not to scale.

Contributors and Attributions

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  \( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)