8: Bose Einstein Condensation
- Page ID
- 50560
In Chapter 6 we have already discussed the microscopic many body description of a Bose condensate. In this chapter we focus on the experimental realization of this very specific, interesting and fundamental kind of matter. And we give some insight into its genuinely quantum mechanical characteristics.
De Broglie’s hypothesis from Chapter 1. Particles with spin in magnetic fields from Chapter 5. The material on bosons in Chapter 6.
Introduction
The Bose-Einstein condensate (BEC) is a very specific, interesting and fundamental kind of matter, actually a gas, consisting of atomic particles. It shows up two different genuinely quantum mechanical characteristics simultaneously. One of them is the wave like nature of massive atoms, a behaviour becoming more and more explicit at very low temperatures. The other property is that particles with integer intrinsic angular momentum (spin) can in principle all be in the same quantum state. Photons, the quanta of electromagnetic radiation are specific kind of bosons of spin 1, while their rest mass is zero. Satendyra Bose derived Planck’s law by assuming this property, and sent his work to Einstein in 1924, who – recognizing the importance of the idea – recommended the publication of the paper of Bose. Soon after this, in the same year Einstein himself discovered that the derivation can be extended to the case when the gas consists of massive particles (unlike photons) and predicted that an ordinary gas can also be brought in that specific state, that is why it got the name Bose-Einstein condensate. As we said, only particles with integer spin may form a condensate, and such particles are called bosons, in honour of Bose. Electrons and other particles with half integer spin do not show up this behaviour, unless a specific interaction couples them to pairs, so that the pair has integer spin. We come to this point below.
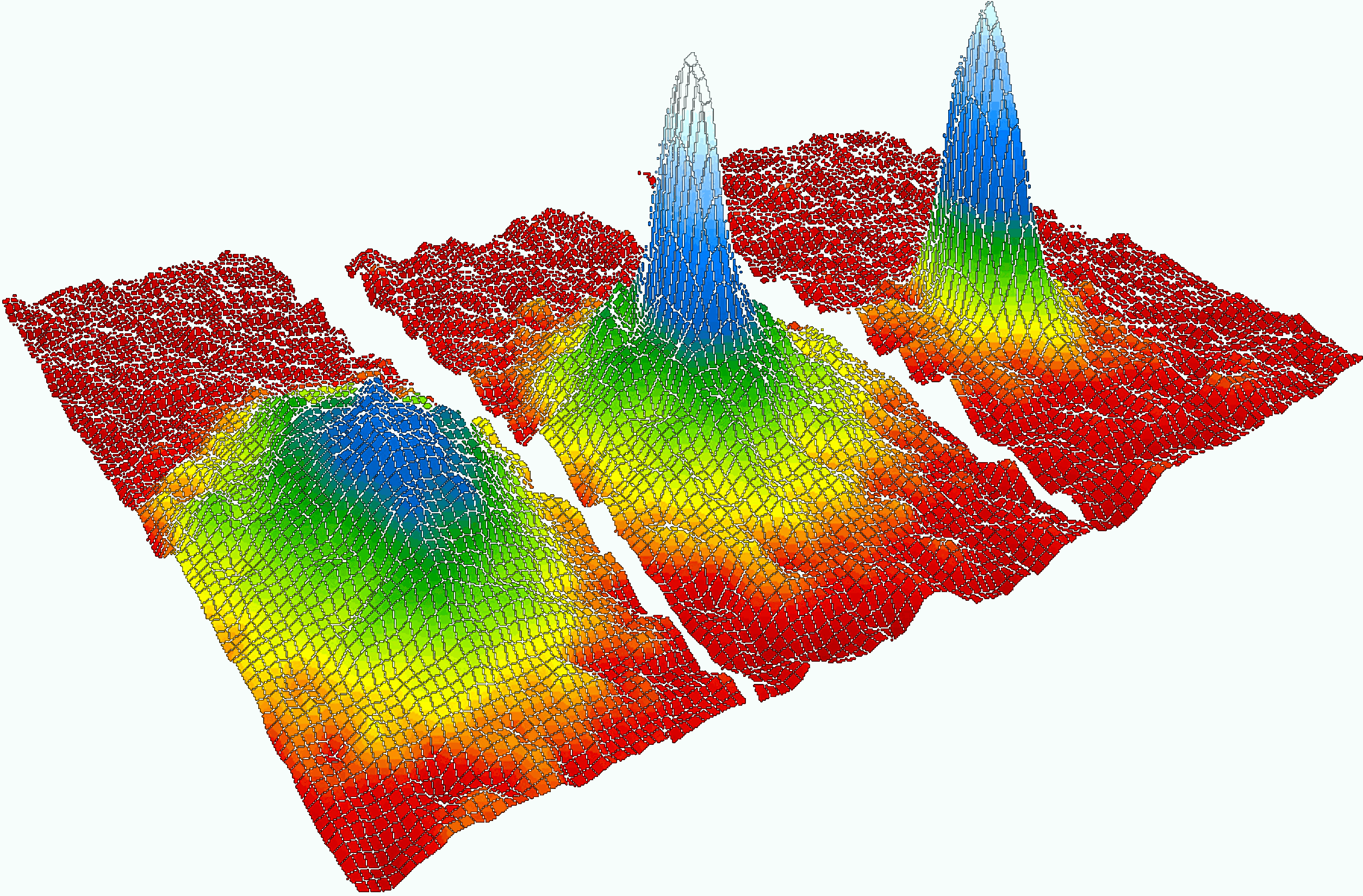
Figure 8.1: Cooling rubidium atoms to less than 170 billionths of a degree above absolute zero caused the individual atoms to condense into a "superatom" behaving as a single entity. The graphic shows three-dimensional successive snap shots in time in which the atoms condensed from less dense red, yellow and green areas into very dense blue to white areas.
http://en.Wikipedia.org/wiki/Bose_Einstein_condensate
Predicted 1924 …Created 1995. Check out the BEC Homepage for introductory level lessons on BEC with animations, explaining the physics behind.
http://www.colorado.edu/physics/2000/bec/
In chapter 6 we have already discussed the microscopic many body description of a Bose condensate. We repeat it here shortly: The independent particles are all in their identical lowest energy one particle state, i.e. in their ground state. The corresponding total wave function is:
\(\Psi_{0}\left(\xi_{1}, \xi_{2}, \ldots, \xi_{N}\right)=\varphi_{0}\left(\xi_{1}\right) \varphi_{0}\left(\xi_{2}\right) \ldots \varphi_{0}\left(\xi_{N}\right)\) (8.1)
In spite of its name a Bose-Einstein condensate is a dilute ideal, or almost ideal gas. While in air e.g. at atmospheric pressures and room temperatures the number of molecules (\(\mathrm{N}_{2}\) and \(\mathrm{O}_{2}\)) in \(1\mathrm{cm}^{3}\) is \(10^{19}\), in a condensate the density is only \(10^{12}-10^{13} \text { atoms } / \mathrm{cm}^{3}\). In fluids and in solids this concentration is \(10^{22} \text { atoms } / \mathrm{cm}^{3}\) whilst in atomic nuclei the nucleon density is \(10^{38} \text { particles } / \mathrm{cm}^{3}\). Nevertheless at very low temperatures the condensate has very different properties from an ordinary ideal gas. The energy spectrum of the gas is practically continuous, so the excitations are of very low energy, which means that an ultralow temperature is necessary to achieve even the vicinity of the required ground state.
In the present chapter we come to the practical side of the problem and discuss the possibilities of the creation of this state of matter. The most important characteristic is that at appropriately low temperatures atoms lose their individuality and show collective behaviour. We can find the condition when this happens by a relatively simple calculation. The momentum p of the atoms is connected with their de-Broglie wavelength by the formula:
\(p=m v=h / \lambda_{d B}, \quad \text { or } \quad \lambda_{d B}=h / m v\) (8.2)
The velocity depends on the temperature, or more precisely, thinking of the classical ideal gas, we have from the equipartition theorem the equation \(m\nu^{2}/2=3k_{B}T/2\), where \(\nu\) is the average velocity of the particles, and \(k_{B}\) is the Boltzmann constant. Then we get the momentum and the thermal de Broglie wavelength according to:
\(v=\sqrt{\frac{3 k_{B} T}{m}}, \quad p=m v=\sqrt{3 k_{B} T m}\) (8.3)
\(\lambda_{d B}=\frac{h}{p}=\frac{h}{\sqrt{3 k_{B} T m}}\) (8.4)
This latter length scale is where the wave-like properties of the particles do manifest. At room temperatures this length is very small, but it increases with lowering the absolute temperature. If we consider a particle in a vessel of volume V containing \(N_{0}\) atoms, the density of the particles is \(n=N_{0}/V\), and its inverse is the volume shared by a single particle on the average: \(V/N_{0}=n^{−1}\). The linear size of a corresponding cube is \(n^{-1 / 3}=\sqrt[3]{V / N_{0}}\). Assume that by cooling the gas we can achieve a \(λ_{T}\) which is of the order of the distance between the particles \(n^{−1/3}\). At this value of the temperature we expect that the individuality of the particles is lost, and collective quantum mechanical phenomena appear. The condition of this, with the above simple reasoning is the fulfillment of the inequality
\(n^{1 / 3} \lambda_{T}=n^{1 / 3} \frac{h}{\sqrt{3 k T m}} \gtrsim 1\) (8.5)
In order to get such a gas there seem to be two possibilities. One of them is to increase n, i.e. the density of the atoms. But a simple calculation shows that at milikelvin temperatures, attainable with traditional cooling technologies this would mean a density \(n=10^{28}\mathrm{m}^{-3}\) which is the density of a fluid or a solid. Therefore the sample would be very far from an ideal gas, like the Bose condensate, which assumes that there is no direct interaction between the particles. So the effect will certainly be masked by the strong interaction between the constituent particles.
Calculate the number density (concentration) of the H gas and a \({ }_{11}^{23} \mathrm{Na}\) gas at \(0^{\circ} \mathrm{C}\) and atmospheric pressure. Use the universal gas law. For an atomic gas of Hydrogen the mass of a single atom is essentially that of the proton, \(1.66×10^{−27}\mathrm{kg}\), the mass of the \({ }_{11}^{23} \mathrm{Na}\) atom is about 23 times larger \(3.8×10^{−27}\mathrm{kg}\).
There is one exception, where there is some remnant trace of the quantum effect following from the Bose statistics, and this is the isotope \({ }_{2}^{4} \mathrm{He}\). This material becomes a fluid at \(4.2\mathrm{K}\) at normal pressures, so by no means can it be considered to be an ideal gas. Still, when cooling it further, below \(2.18\mathrm{K}\) it shows strange properties, the most surprising of which is superfluidity. The effect was discovered in 1937 by Pyotr Kapitsa in Moscow, and by John Allen and his co-worker Don Misener in Cambridge (England). In the case of He the mass mm is relatively small, which according to (8.5) shows that in this material the unusual properties could be connected with Bose-Einstein condensation. This was first suggested by Fritz London in 1938. By the middle of the 20th century it became widely accepted among physicists that the very complicated phase transition of He at \(2.18\mathrm{K}\) is a kind of a Bose-Einstein condensation, which however does not appear in its clean form, because it is veiled by the weak, but still existing interaction between the atoms of He.
Is it possible in principle to observe Bose Einstein condensation in Hydrogen? Why is that liquid He shows a somewhat related effect, while H, which is 4 times lighter is not a superfluid?
As we have noted Bose condensation appears only for bosons which have integer spin. However at even lower temperatures fermions can also form specific kinds of a condensates. A necessary condition for this is the formation of pairs: a pair of fermions is a boson, as the spin of the pair is then an integer. This is the reason of superconductivity, where a pair of electrons, called a Cooper pair is formed, and the effect of superconductivity can be considered to be a kind of superfluidity of these pairs. In the case of superconductivity the weak attractive force between the electrons is created indirectly through their interaction with the motion of the ions of the crystal lattice. J. Bardeen, L. Cooper and R. Schrieffer won the Nobel prize in 1972 for their microscopic explanation of superconductivity in 1957.
Under this link you can fin the details of the 1972 Nobel Prize in Physics won by John Bardeen, Leon N. Cooper and Robert Schrieffer for their microscopic explanation of superconductivity.
http://www.nobelprize.org/nobel_prizes/physics/laureates/1972/
Another example is the isotope \({ }_{2}^{3} \mathrm{He}\), which is a fermion, having only one neutron in its nucleus instead of two as in \({ }_{2}^{4} \mathrm{He}\). It was observed that \({ }_{2}^{3} \mathrm{He}\) also shows superfluidity below at \(2.5\mathrm{mK}\), which is three orders of magnitude lower than that of its bosonic variant. Here again these atoms may form pairs at these very low temperatures which is necessary for the stability of the very weak coupling of the pair. D. Lee, D. Osheroff and R. C. Richardson won the 1996 Nobel Prize in Physics for their discovery this effect, and A. Legget in 2003 for its theoretical explanation.
Under this link you can fin the details of the 1996 Nobel Prize in Physics won by D. Lee, D. Osheroff and R. C. Richardson for their or their discovery of superfluidity in helium-3.
http://www.nobelprize.org/nobel_prizes/physics/laureates/1996/
Under this link you can fin the details of the 2003 Nobel Prize in Physics won by Alexei A. Abrikosov, Vitaly L. Ginzburg and Anthony J. Leggett for their pioneering contributions to the theory of superconductors and superfluids.
http://www.nobelprize.org/nobel_prizes/physics/laureates/2003/
Atoms that can exhibit BE Condensation
A simple rule to decide if an ordinary atom is a fermion or a boson is to count the number of its elementary fermion constituents. The spin of all atomic constituents (electrons, protons, neutrons) is half integer so if the number of the nuclei+electrons is even then the atom is a boson. If this number is odd then the atom is a fermion. (We note here in addition, that at a more elementary level the spin \(1/2\) of the nucleons is a result of adding the spins of the three quarks each possessing a spin value \(1/2\).)
So one of the candidates that seemed appropriate to create a condensate was the gas of \({ }_{11}^{23} \mathrm{Na}\) atoms. It has 11 electrons, 11 protons and 12 neutrons so their spin must add up to an integer. In addition, due to the large transition dipole moment of the Na D line (doublet) of the transition around 589 nm, it can be effectively manipulated by optical methods.
In more detail: 10 of the electrons of this atom form a closed configuration filling the \(n=1\) and \(n=2\) shells, similar to the 10 electrons of Ne, and resulting in zero spin. The 11-th electron of spin \(s=1/2\) causes the half integer spin of the electron cloud of Na, resulting in the \(3^{2}S_{1/2}\) state. This symbol – as usual – corresponds to the notation \(n^{2s+1}L_{j}\) meaning that the highest energy electron is on a shell with principal quantum number \(n=3\), the spin multiplicity is \(2s+1=2\), the orbital angular momentum of the valence electrons is a state with \(L=0\), i.e a centrally symmetric SS state, the total angular momentum is \(J=1/2\) that comes from \(J=L+S\). The 23 nucleons (11 protons + 12 neutrons) in its nucleus, has each a spin of 1/2. As 23 is an odd number the nuclear spin must add up to a half integer, and its value is actually \(I=3/2\). It turns out that the total spin of the atom is either \(F=1\) resulting from \(|I−J|\) or \(F=2\), resulting from \(I+J\). So the total spin is an integer, the \({ }_{11}^{23} \mathrm{Na}\) atoms are bosons.
Which of the two isotopes of \({ }_{3}^{6} \mathrm{Li}\) and \({ }_{3}^{7} \mathrm{Li}\) is a boson and which is a fermion?
Experimental observation of BEC
The main task is to achieve the low temperature necessary for the formation of a condensate. The first step is optical or Doppler cooling of the atoms with light.
Assume that a light of frequency \(\nu=ω/2π=c/λ\) is shone on a gas of atoms that is on resonance with one of the atomic transitions. The photons have energy \(ℏω\) and a momentum \(2πℏ/λ=ℏk\). The atom of mass mm absorbing a photon will have a different velocity it had before the absorption, because of momentum conservation. If the atom has a momentum opposite to the one of the photon, i.e. they move into opposite directions, then after absorption the velocity of the atom will be smaller by the very small value \(ℏk/m=hν/mc\) because
\(m \nu^{\prime}=m \nu-\hbar k\) (8.6)
But atoms moving in the opposite direction as the photon absorb at frequencies \(ω=ω_{0}−kv\).
The atom absorbs the energy \(ℏω\), gets excited, and soon after emits again the photon, which causes a recoil again. But the direction of the emitted photon is randomly distributed in the whole \(4π\) solid angle. If the atom undergoes many cycles of absorption and emission during its interaction with the laser beam, the time average over the momentum obtained during emission will be zero while the one obtained in the absorption process is always negative, at least for the atoms moving opposite to the laser beam. Therefore the net result is a loss of momentum and a loss of kinetic energy of the atoms, which means that the temperature of the gas as a whole will be lower. It can be shown by formal mathematical arguments that the effect of Doppler cooling can be expressed as a velocity dependent friction force
\(\mathbf{F}=-a \mathbf{v}\) (8.7)
where the constant aa is proportional to the absorption rate and to the detuning \(Δ=ω−ω_{0}\), where \(ω\) is the laser frequency and \(ω_{0}\) is the transition frequency of the atom at rest.
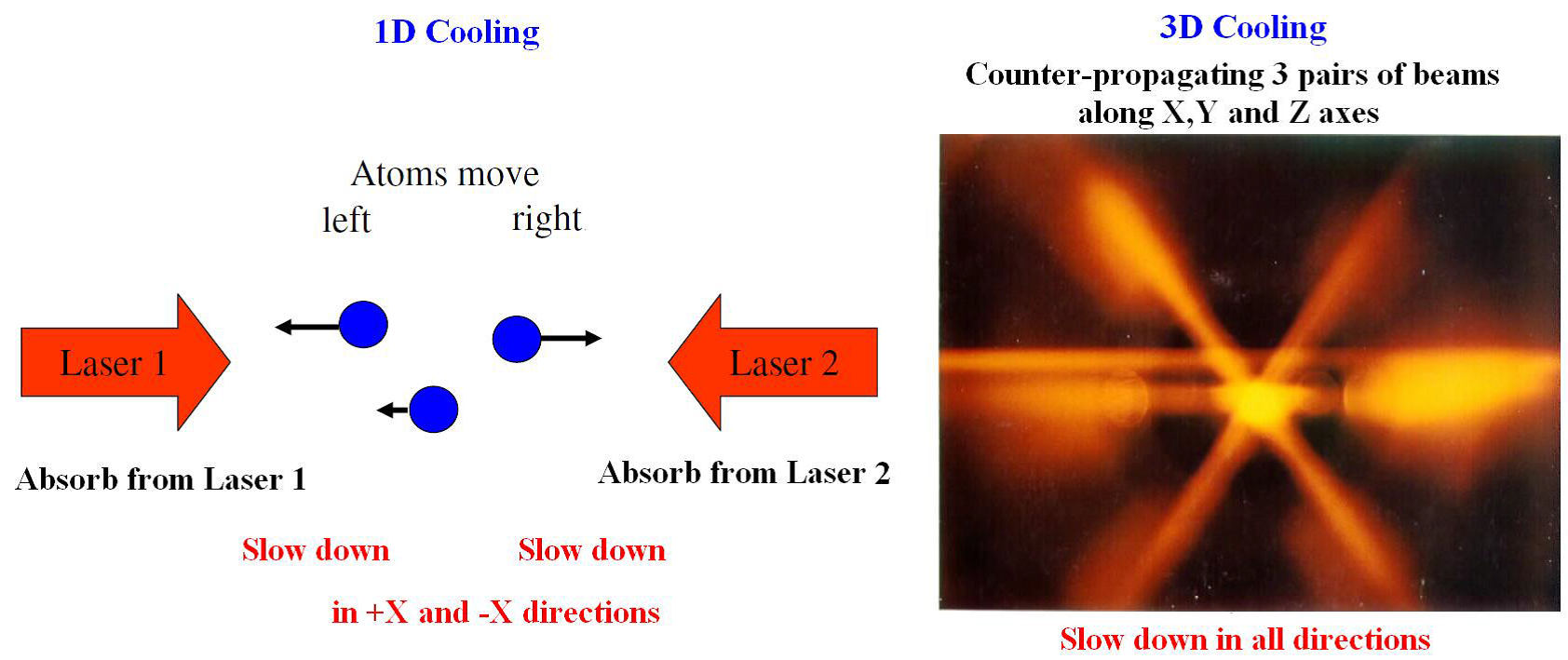
Figure 8.2
Find the average thermal velocity of a Na atom in a gas at room temperature.
The optical cooling uses the \(589.16\mathrm{nm}\) wavelength \(D_{2}\) line corresponding to the \(3 P_{3 / 2}(F=3) \longrightarrow 3 S_{1 / 2}(F=2)\) transition for which the spontaneous lifetime is \(au_{0}=16\mathrm{ns}\).
How many photons are to be absorbed by a sodium atom to bring it to rest?
How long does it take?
How much is the deceleration of the atom, compared with the gravitational acceleration?
What is the deceleration path length of the atom?
During the deceleration process the frequency of the pump laser has to be tuned to \(ω=ω_{0}−k\nu\), because of the Doppler shift. Here \(ω_{0}\) is the circular frequency of the absorption line for an atom at rest. The required value is achieved either by tuning the exciting laser frequency, or by tuning \(ω_{0}\) with a magnetic field via the Zeeman effect.
What we have discussed here corresponds to a one dimensional motion and a one dimensional cooling. In reality the atoms move in all three spatial directions which makes it necessary to apply six laser fields coming from all different orthogonal directions and achieving the deceleration of all three components of the velocity, see Fig 8.3 (b) with additional details.
Magnetooptical Trapping of Atoms
Optical cooling decreases the velocities of atoms in the atomic cloud, but that is only the initial stage of the process. In order to achieve a sufficiently deep temperature additional tricks must be applied. This can be achieved in the device called a magneto-optical trap (MOT), illustrated in Fig.8.3 (a). The MOT consists of a pair of so called anti-Helmholtz coils through which a current is sent into opposite directions. With the zz-axis as the symmetry axis, the magnetic field produced by the coils in the vicinity of the trap centre at \(z=0\) is \(B(z)=bz\) as it follows from the law of Biot and Savart.
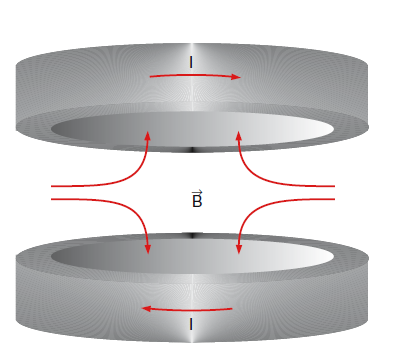
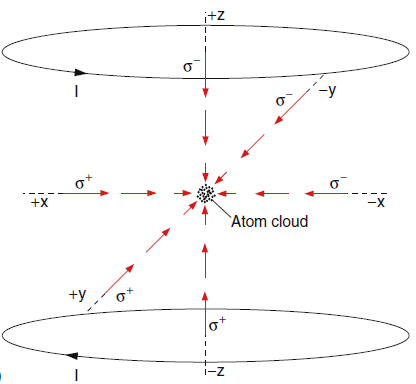
So the magnetic field is zero at the centre \(z=0\), and increases linearly with increasing distance from the centre The field lines are indicated as red curves in Fig. 8.3 (a). In the magnetic field the atomic energy levels experience a splitting into Zeeman components with the energies
\(\varepsilon(B)=-\mathfrak{m} \cdot \mathbf{B}=g_{F} \mu_{B} m_{F}|\mathbf{B}|\) (8.8)
Here \(μ_{B}\) is the Bohr-magneton, \(m_{F}\) is the magnetic quantum number belonging to the total angular momentum \(\mathbf{F}\) (including nuclear spin) of the atom.
The six laser beams passing through the MOT are circularly polarized, carrying an angular momentum ±ℏ±ℏ, and therefore they induce transitions with \(Δm_{F}=±1\). If the laser frequency \(ω_{L}\) is below the resonance frequency \(ω_{0}\), atoms in the region \(z>0\) absorb preferentially \(σ_{−}\) light with negative helicity, and inducing \(Δm_{F}=−1\) transitions, while for \(z<0\) mainly \(σ_{+}\) light is absorbed. For \(z=0\) the absorption rates for both polarization is equal. This pushes all atoms moving outwards back towards the centre The gas of cold molecules is therefore compressed into a dense cloud around the centre of the MOT. It can be shown, that the resulting force is one that pushes the atoms from all directions towards the centre of the MOT, and the potential is like a harmonic potential trapping the atoms around the centre. Taking into account the braking force due to the Doppler effect as discussed in the previous subsection the total force acting on the atoms will be:
\(F_{z}=-D z-a \nu_{z}\) (8.9)
resulting in a damped oscillation of the atoms with mass M around the trap centre with a frequency and damping constant
\(\Omega=D / M, \quad \beta=a / M\) (8.10)
EXAMPLE:
For Rubidium atoms with \(M=1.4×10^{−25}\mathrm{kg}\) the absorption wavelength is \(λ=785\mathrm{nm}\), corresponding to \(k=8×10^{6}\mathrm{m}^{−1}\). With a laser detuning \(δ=γ\) and an absorption rate \(R_{0}=γ/2\) one obtains \(a=4×10^{−21}\mathrm{Ns/m}\). With a magnetic field gradient \(b=0.1T/m\) and the magnetic moment \(\\mathfrak{m} \approx \mu \mathbf{B}\) the constant \(D=2.37×10^{−18}\) can be calculated. This gives the oscillation frequency \(ω=4100\mathrm{s}^{−1}\) and the damping constant \(β=1.2×10^{−2}\mathrm{s}^{−1}\). The atoms relax with a time constant of \(12\mathrm{ms}\) after about 50 oscillation periods against the trap centre. Up to now we have only regarded the movement of the atoms in the z direction. For the x and y directions, similar considerations hold.
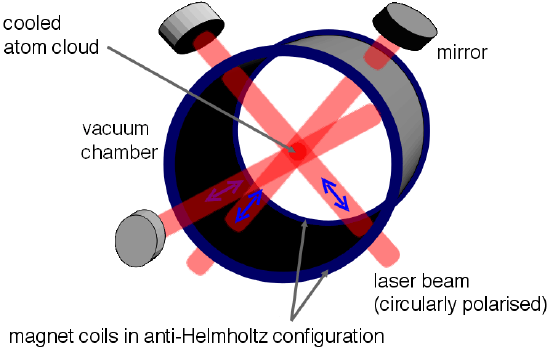
Figure 8.4: An experimental setup of a magneto-optical trap.
http://en.Wikipedia.org/wiki/File:MOT_setup.png

Figure 8.5: A magneto-optical trap in real laboratory situation.
http://phet.colorado.edu/hu/contributions/view/3104
Evaporation cooling
It turns out however that the temperature reached by Doppler plus magnetooptical cooling is still not low enough to reach the critical temperature for BEC. Therefore, an additional cooling technique has to be applied. This method is called evaporation cooling. It is in principle the same technique one uses for cooling a hot cup of coffee by blowing over the liquid surface. This removes the fastest molecules in the vaporous phase above the surface and decreases the average kinetic energy, i.e., the temperature of the remaining molecules.
In order to apply this technique the cold atoms are transferred from a MOT to a pure magnetic trap that has no cooling lasers, by pushing them with a laser beam into the wanted direction. In this trap that is formed by an inhomogeneous magnetic field, they are kept not by the recoil forces of lasers like in the MOT, but by the magnetic force \(F=-(\mathfrak{m} \nabla) \mathbf{B}\) due to their magnetic moment \(\mathfrak{m}\). Although this force is much smaller than the recoil force, the atoms, which are now already very cold, can be trapped since their kinetic energy is small. Here they have the potential energy \(E_{p o t}=-\mathfrak{m} \mathbf{B}\). Due to the distribution of their kinetic (thermal) energy they fill the trap potential up to a certain maximal energy \(E_{max}\). Now the trap is irradiated by a radio-frequency wave that induces flips of the atomic spin, when its frequency \(\nu_{rf}=ΔE/h\) matches the energy difference
\(\Delta E=E_{\uparrow}-E_{\downarrow}\) (8.11)
The atoms that have suffered a spin flip are automatically pushed out of the trap because their potential is now repulsive Choosing the frequency in such a way that only the hottest atoms can make a spin flip, results in a decrease of the mean energy of the trapped atoms.
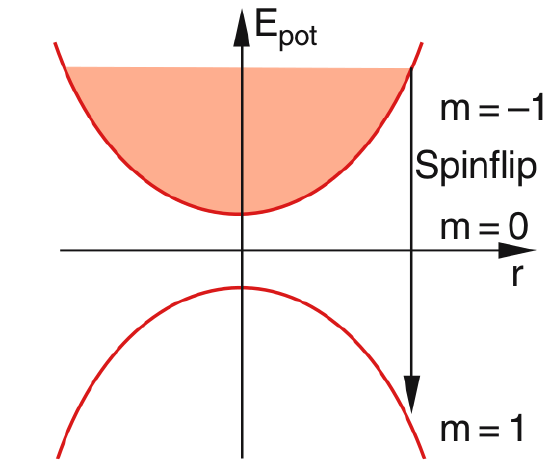
During the evaporation of atoms, the temperature drops below the critical temperature. The radial density profile of the atoms becomes very narrow because all atoms condense into the lowest potential energy state of the magnetic trap. This can be monitored by sending a widened weak laser beam through the condensate, which is partly absorbed. With a CCD-array, the transmitted intensity is detected, which is a measure of the spatial dependence of the absorption and thus of the density of atoms.
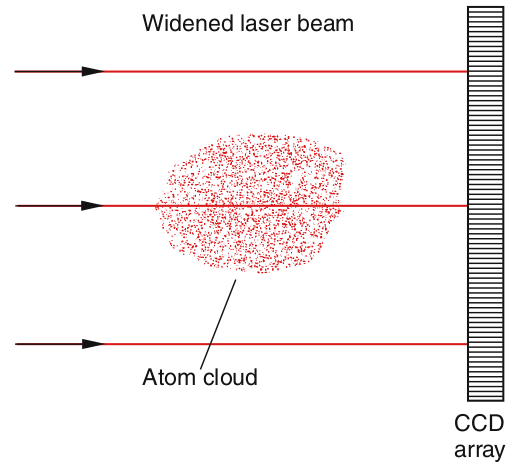
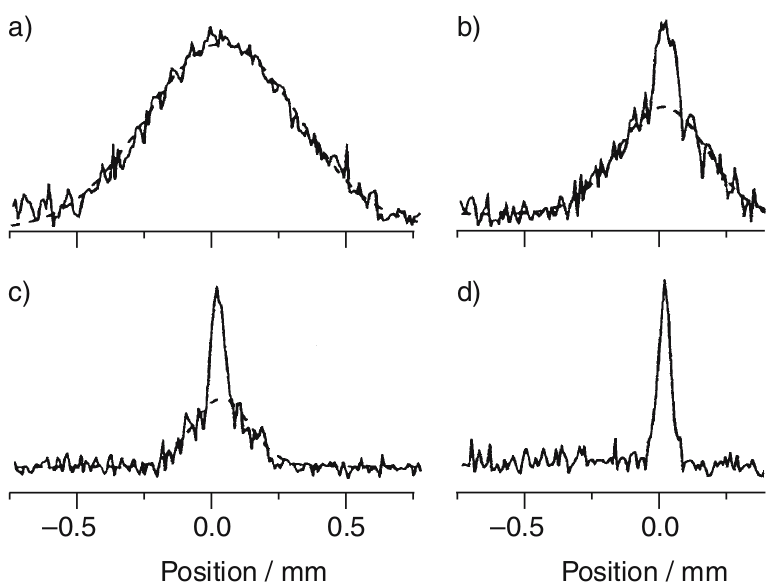
Figure 8.7: Monitoring BEC by the spatial absorption profile of the transmitted probe laser. Density profiles of atomic cloud with \(T=1.2μ\mathrm{K}\) (a), \(310\mathrm{nK}\) (b), \(170\mathrm{nK}\) (c), and below the critical temperature of BEC (d)
By this technique the first experimental proof of Bose–Einstein condensation was reported in 1996 by E. Cornell and C. Wieman in Boulder, Colorado and independently by W. Ketterle and his group at the MIT in Cambridge near Boston. The group leaders received the Nobel Prize in 2001.
Under this link you can find a lot of additional information on Eric A. Cornell, Wolfgang Ketterle and Carl E. Wieman the Physics Nobel Prize winners of 2001, including interviews and their Nobel Lectures.
http://www.nobelprize.org/nobel_prizes/physics/laureates/2001/
The BEC behaves in many aspects like a supraliquid with zero viscosity. Spectroscopy of atoms in a Bose–Einstein condensate gives a lot of information on collective effects of many atoms, which are all in the same state. One of the fascinating effects is the release of a coherent beam of atoms out of the BEC. Such a coherent beam represents a large flux of atoms that all have nearly the same energy. Because of its resemblance to a coherent beam of photons, which is a laser beam, it is called an atom laser. Two beams from the same BEC can interfere with each other if they are spatially overlapping.
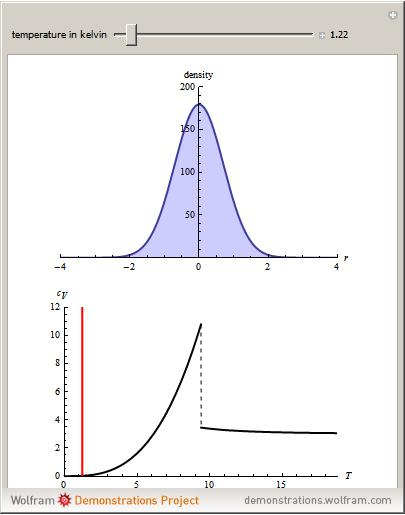
At ultra-cold temperatures, a gas of bosons undergoes a phase transition where there is a macroscopic occupation of the ground state. The top plot shows how the density profile of bosons in a 3D harmonic trap changes with temperature TT.
http://demonstrations.wolfram.com/BoseEinsteinCondensationInAHarmonicTrap/
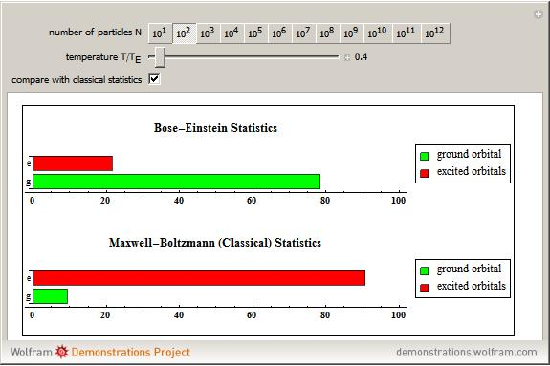
This Demonstration shows the thermal population of the ground orbital and all the excited orbitals for a gas of N free bosons as a function of temperature. The populations according to the classical Maxwell-Boltzmann statistics can also be shown. The temperature is measured in units of Einstein’s condensation temperature.
http://demonstrations.wolfram.com/BoseEinsteinCondensationFreeBosonGas/