7.6: Spherical Harmonics

The simultaneous eigenstates, \(Y_{l,m}(\theta,\phi)\), of \(L^2\) and \(L_z\) are known as the spherical harmonics . Let us investigate their functional form.

We know that \[L_+\,Y_{l,l}(\theta,\phi) = 0,\] because there is no state for which \(m\) has a larger value than \(+l\). Writing \[Y_{l,l}(\theta,\phi) = {\mit\Theta}_{l,l}(\theta)\,{\rm e}^{\,{\rm i}\,l\,\phi}\] [see Equations ([e8.34]) and ([e8.38])], and making use of Equation ([e8.28]), we obtain

\[\hbar\,{\rm e}^{\,{\rm i}\,\phi}\left(\frac{\partial}{\partial\theta} + {\rm i}\,\cot\theta\,\frac{\partial}{\partial\phi}\right){\mit\Theta}_{l,l}(\theta)\,{\rm e}^{\,i\,l\,\phi}=0.\]

This equation yields \[\frac{d{\mit\Theta}_{l,l}}{d\theta} - l\,\cot\theta\,{\mit\Theta}_{l,l} = 0.\] which can easily be solved to give \[{\mit\Theta}_{l,l}\sim (\sin\theta)^{\,l}.\] Hence, we conclude that

\[\label{e8.59} Y_{l,l}(\theta,\phi) \sim (\sin\theta)^{\,l}\,{\rm e}^{\,{\rm i}\,l\,\phi}.\]

Likewise, it is easy to demonstrate that

\[\label{e8.60} Y_{l,-l}(\theta,\phi) \sim (\sin\theta)^{\,l}\,{\rm e}^{-{\rm i}\,l\,\phi}.\]

Once we know \(Y_{l,l}\), we can obtain \(Y_{l,l-1}\) by operating on \(Y_{l,l}\) with the lowering operator \(L_-\). Thus,

\[Y_{l,l-1} \sim L_-\,Y_{l,l} \sim {\rm e}^{-{\rm i}\,\phi}\left(-\frac{\partial}{\partial\theta} + {\rm i}\,\cot\theta\,\frac{\partial}{\partial\phi}\right) (\sin\theta)^{\,l}\,{\rm e}^{\,{\rm i}\,l\,\phi},\]

where use has been made of Equation ([e8.28]). The previous equation yields \[Y_{l,l-1}\sim {\rm e}^{\,{\rm i}\,(l-1)\,\phi}\left(\frac{d}{d\theta} +l\,\cot\theta\right)(\sin\theta)^{\,l}.\]

Now, \[\label{e8.64} \left(\frac{d}{d\theta}+l\,\cot\theta\right)f(\theta)\equiv \frac{1}{(\sin\theta)^{\,l}}\frac{d}{d\theta}\left[ (\sin\theta)^{\,l}\,f(\theta)\right],\] where \(f(\theta)\) is a general function. Hence, we can write

\[\label{e8.64a} Y_{l,l-1}(\theta,\phi)\sim \frac{ {\rm e}^{\,{\rm i}\,(l-1)\,\phi}}{(\sin\theta)^{\,l-1}}\left(\frac{1}{\sin\theta}\frac{d}{d\theta}\right) (\sin\theta)^{2\,l}.\]

ikewise, we can show that

\[\label{e8.65} Y_{l,-l+1}(\theta,\phi)\sim L_+\,Y_{l,-l}\sim \frac{ {\rm e}^{-{\rm i}\,(l-1)\,\phi}}{(\sin\theta)^{\,l-1}}\left(\frac{1}{\sin\theta}\frac{d}{d\theta}\right) (\sin\theta)^{2\,l}.\]

We can now obtain \(Y_{l,l-2}\) by operating on \(Y_{l,l-1}\) with the lowering operator. We get

\[Y_{l,l-2}\sim L_-\,Y_{l,l-1}\sim {\rm e}^{-{\rm i}\,\phi}\left(-\frac{\partial}{\partial\theta} + {\rm i}\,\cot\theta\,\frac{\partial}{\partial\phi}\right) \frac{ {\rm e}^{\,{\rm i}\,(l-1)\,\phi}}{(\sin\theta)^{\,l-1}}\left(\frac{1}{\sin\theta}\frac{d}{d\theta}\right) (\sin\theta)^{2\,l},\]

which reduces to \[Y_{l,l-2}\sim {\rm e}^{-{\rm i}\,(l-2)\,\phi}\left[\frac{d}{d\theta} +(l-1)\,\cot\theta\right] \frac{1}{(\sin\theta)^{\,l-1}}\left(\frac{1}{\sin\theta}\frac{d}{d\theta}\right) (\sin\theta)^{2\,l}.\] Finally, making use of Equation ([e8.64]), we obtain

\[\label{e8.68} Y_{l,l-2}(\theta,\phi) \sim \frac{ {\rm e}^{\,{\rm i}\,(l-2)\,\phi}}{(\sin\theta)^{\,l-2}}\left(\frac{1}{\sin\theta}\frac{d}{d\theta}\right)^2 (\sin\theta)^{2\,l}.\] Likewise, we can show that

\[\label{e8.69} Y_{l,-l+2}(\theta,\phi) \sim L_+\,Y_{l,-l+1}\sim \frac{ {\rm e}^{-{\rm i}\,(l-2)\,\phi}}{(\sin\theta)^{\,l-2}}\left(\frac{1}{\sin\theta}\frac{d}{d\theta}\right)^2 (\sin\theta)^{2\,l}.\]

A comparison of Equations ([e8.59]), ([e8.64a]), and ([e8.68]) reveals the general functional form of the spherical harmonics:

\[Y_{l,m}(\theta,\phi)\sim \frac{ {\rm e}^{\,{\rm i}\,m\,\phi}}{(\sin\theta)^{\,m}}\left(\frac{1}{\sin\theta}\frac{d}{d\theta}\right)^{l-m} (\sin\theta)^{2\,l}.\]

Here, \(m\) is assumed to be non-negative. Making the substitution \(u=\cos\theta\), we can also write

\[Y_{l,m}(u,\phi)\sim {\rm e}^{\,{\rm i}\,m\,\phi}\,(1-u^{\,2})^{-m/2}\left(\frac{d}{d u}\right)^{l-m} (1-u^{\,2})^{\,l}.\]

Finally, it is clear from Equations ([e8.60]), ([e8.65]), and ([e8.69]) that

\[Y_{l,-m} \sim Y^{\,\ast}_{l,m}.\]

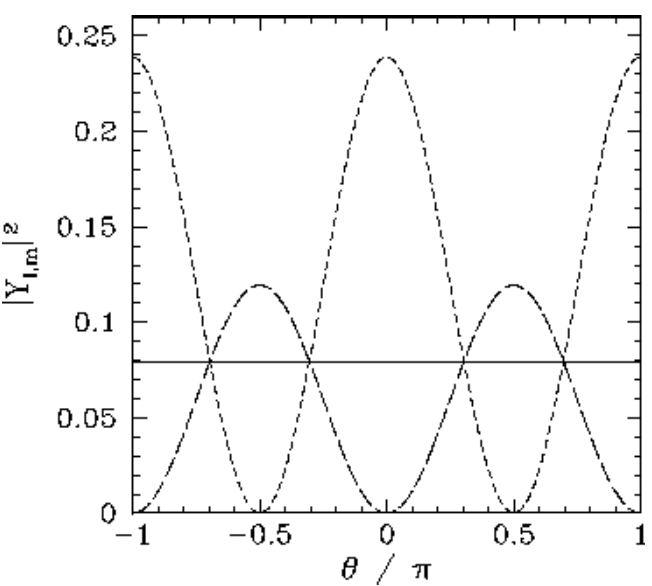
Figure 18: The \(\begin{equation}\left|Y_{l, m}(\theta, \phi)\right|^{2}\end{equation}\) plotted as a functions of \(\theta\). The solid, short-dashed, and long-dashed curves correspond to \(\begin{equation}l, m=0,0, \text { and } 1,0, \text { and } 1,\pm 1\end{equation}\), respectively.

We now need to normalize our spherical harmonic functions so as to ensure that \[\oint |Y_{l,m}(\theta,\phi)|^{\,2}\,d{\mit\Omega} = 1.\] After a great deal of tedious analysis, the normalized spherical harmonic functions are found to take the form \[Y_{l,m}(\theta,\phi) =(-1)^m\, \left[\frac{2\,l+1}{4\pi}\,\frac{(l-m)!}{(l+m)!}\right]^{1/2} P_{l,m}(\cos\theta)\,{\rm e}^{\,{\rm i}\,m\,\phi}\] for \(m\geq 0\), where the \(P_{l,m}\) are known as associated Legendre polynomials , and are written \[P_{l,m}(u) = (-1)^{l+m}\,\frac{(l+m)!}{(l-m)!}\,\frac{(1-u^{\,2})^{-m/2}}{2^l\,l!}\left(\frac{d}{du}\right)^{l-m} (1-u^{\,2})^{\,l}\] for \(m\geq 0\). Alternatively, \[P_{l,m}(u) = (-1)^{l}\,\frac{(1-u^{\,2})^{m/2}}{2^l\,l!}\left(\frac{d}{du}\right)^{l+m} (1-u^{\,2})^{\,l},\] for \(m\geq 0\). The spherical harmonics characterized by \(m<0\) can be calculated from those characterized by \(m>0\) via the identity \[Y_{l,-m} = (-1)^m\,Y^{\,\ast}_{l,m}.\] The spherical harmonics are orthonormal: that is, \[\label{spho} \oint Y_{l',m'}^{\,\ast}\,Y_{l,m}\,d{\mit\Omega} = \delta_{ll'}\,\delta_{mm'},\] and also form a complete set. In other words, any well-behaved function of \(\theta\) and \(\phi\) can be represented as a superposition of spherical harmonics. Finally, and most importantly, the spherical harmonics are the simultaneous eigenstates of \(L_z\) and \(L^2\) corresponding to the eigenvalues \(m\,\hbar\) and \(l\,(l+1)\,\hbar^{\,2}\), respectively.

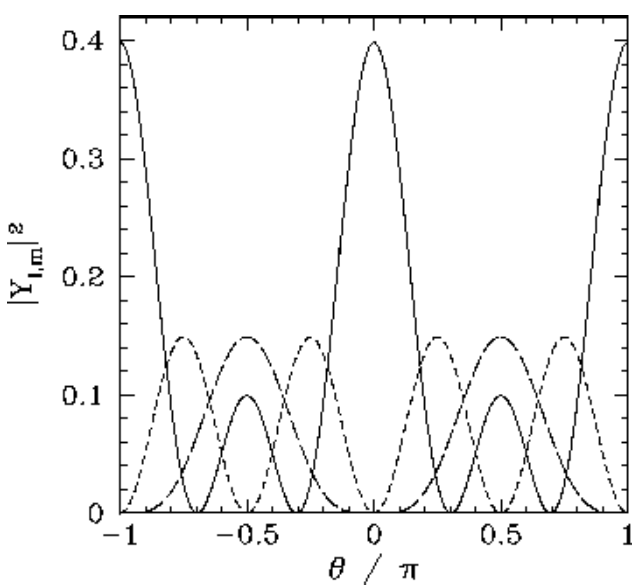
Figure 19: The \(\begin{equation}\left|Y_{l, m}(\theta, \phi)\right|^{2}\end{equation}\) plotted as a functions of  \(\theta\). The solid, short-dashed, and long-dashed curves correspond to  \(\begin{equation}l, m=2,0, \text { and } 2,\pm 1, \text { and } 2,\pm 2\end{equation}\) respectively.

All of the \(l=0\), \(l=1\), and \(l=2\) spherical harmonics are listed below: \[\begin{aligned} Y_{0,0} &=\frac{1}{\sqrt{4\pi}},\\[0.5ex] Y_{1,0} &= \sqrt{\frac{3}{4\pi}}\,\cos\theta,\\[0.5ex] Y_{1,\pm1} &= \mp \sqrt{\frac{3}{8\pi}}\,\sin\theta\,{\rm e}^{\pm{\rm i}\,\phi},\\[0.5ex] Y_{2,0} &= \sqrt{\frac{5}{16\pi}}\,(3\,\cos^2\theta - 1),\\[0.5ex] Y_{2,\pm 1}&=\mp\sqrt{\frac{15}{8\pi}}\,\sin\theta\,\cos\theta\,{\rm e}^{\pm{\rm i}\,\phi},\\[0.5ex] Y_{2,\pm 2}&= \sqrt{\frac{15}{32\pi}}\,\sin^2\theta\,{\rm e}^{\pm 2\,{\rm i}\,\phi}.\end{aligned}\] The \(\theta\) variation of these functions is illustrated in Figures [ylm1] and [ylm2].

Contributors and Attributions

• Richard Fitzpatrick (Professor of Physics, The University of Texas at Austin)

  \( \newcommand {\ltapp} {\stackrel {_{\normalsize<}}{_{\normalsize \sim}}}\) \(\newcommand {\gtapp} {\stackrel {_{\normalsize>}}{_{\normalsize \sim}}}\) \(\newcommand {\btau}{\mbox{\boldmath$\tau$}}\) \(\newcommand {\bmu}{\mbox{\boldmath$\mu$}}\) \(\newcommand {\bsigma}{\mbox{\boldmath$\sigma$}}\) \(\newcommand {\bOmega}{\mbox{\boldmath$\Omega$}}\) \(\newcommand {\bomega}{\mbox{\boldmath$\omega$}}\) \(\newcommand {\bepsilon}{\mbox{\boldmath$\epsilon$}}\)