2.3: Function Spaces

Linear Algebra in Infinite Dimensions

The motivation for our review of linear algebra was the observation that the set of solutions to Schrödinger’s equation satisfies some of the basic requirements of a vector space, in that linear combinations of solutions give another solution to the equation. Furthermore, Schrödinger’s equation itself, as a differential operator acting on a function, suggests that the concept of a matrix operator acting on vectors in an n-dimensional vector space can be extended to more general operators, such as differential operators, acting on functions in an infinite-dimensional space.

Our analysis of linear vector spaces began by defining an inner product, which was used to establish an orthonormal basis for the space. Constructing a well-defined basis for the space of all functions on the real axis sounds impossible, and probably is. Fortunately, we don’t need to be so all-encompassing. For one thing, we are not interested in functions with discontinuities, because in quantum mechanics that would be a wavefunction corresponding to infinite energy. (We can allow discontinuities in slope, although, as discussed in the Electron in a Box lecture, that occurs only where the potential is infinite. Infinite potentials are of course unphysical, but are convenient approximations in some cases, so we’ll keep that option open.) Another important restriction arises from the requirement that the wavefunction describe a single particle—it must be normalizable, that is to say the norm

\[ \int_{-\infty}^{\infty} \psi^*(x)\psi(x)dx <\infty \label{2.3.1}\]

and in fact \(\psi\) must be scaled so that this integral is equal to unity for actual computation of probabilities. Note that \(\psi(x)\) means \(\psi(x,t=0)\), but the norm turns out to be time-independent, as it must be, for the case of a single particle.

Building on the analogy with n-dimensional vector spaces, the requirement of finite norm suggests a definition for the inner product in function space: \[ \langle f|g\rangle=\int_{-\infty}^{\infty} f^*(x)g(x)dx \label{2.3.2}\]

This definition satisfies Dirac’s requirement that \(\langle f|g\rangle^*=\langle g|f\rangle\), gives a positive norm, and is linear in \(f,\; g\). The space of functions with this inner product, and with finite norm \(\sqrt{\langle f|f\rangle}\), is written \(L_2(-\infty,\infty)\) or just \(L_2\). The functions are said to be “square integrable”.

Notice that this inner product resembles the linear algebraic bra-ket product if we imagine every point on the line as an independent basis vector—mathematically meaningless, of course, but a hint of where we’re going.

Electron in a Box Again

As a preliminary to discussing functions on the infinite line, it is worth considering those restricted to the finite interval \((0, L)\) and vanishing at the two ends. These are precisely the conditions satisfied by the electron-in-a-box wavefunctions (see the earlier lecture):

\[ |n\rangle=\psi_n(x,t=0)=\sqrt{\frac{2}{L}}\sin \frac{n\pi x}{L} \label{2.3.3}\]

Recall from the Fourier Series lecture that any function without discontinuities can be represented as a sum over Fourier components. For the present case of functions equal to zero at the two ends (as any physical wavefunction in a box must be) the sine kets \(|n\rangle\) above form a complete set, that is to say, at \(t = 0\), any \(\psi(x)\) satisfying the boundary condition can be written:

\[ |\psi(x)\rangle=\sum_{n=1}^{\infty} a_n|n\rangle \label{2.3.4}\]

where, from the orthonormality of the basis set \(|n\rangle\), the Fourier coefficients \(a_n=\langle n|\psi\rangle\),so (making explicit that \(\psi(x)\)is in fact a ket in this vector space)

\[ |\psi\rangle=\sum_{n=1}^{\infty} |n\rangle \langle n|\psi\rangle \label{2.3.5}\]

giving an identity operator in the space of continuous functions vanishing at 0 and \(L\):

\[ I=\sum_{n=1}^{\infty} |n\rangle \langle n| \label{2.3.6}\]

exactly analogous to that in finite-dimensional vector spaces. The inner product of two functions

\[ \psi(x)=\sum_{n=1}^{\infty} a_n|n\rangle,\; \phi(x)=\sum_{n=1}^{\infty} b_n|n\rangle \label{2.3.7}\]

defined as in the preceding section by

\[ \langle \phi|\psi\rangle=\int_{-\infty}^{\infty} \phi^*(x)\psi(x)dx \label{2.3.8}\]

is equivalently, in terms of Fourier coefficients, \[ \langle \phi|\psi\rangle=\sum_{n=1}^{\infty} b_n^*a_n \label{2.3.9}\]

and the normalization \[ \langle \psi|\psi\rangle=\int_{-\infty}^{\infty} \psi^*(x)\psi(x)dx=\sum_{n=1}^{\infty} |a_n|^2=1 \label{2.3.10}\]

So for the electron-in-a-box wavefunctions, the orthonormal basis of sine functions gives a well-defined infinite-dimensional vector space.

We have previously stated that the standard interpretation of the wavefunction \(\psi(x)\) is that \(|\psi(x)|^2 dx\) is the probability of finding the particle in a small interval \(dx\) near \(x\), and on integrating over all \(x\) the total probability of finding the particle is one. But we could also look for the particle in a particular state, rather than in a particular small interval \(dx\). In this case, \(|a_n|^2\) is the probability of finding the particle in the \(n^{th}\) state. This is consistent with the previous interpretation, and is parallel to our earlier analysis of the probability of a particle having a particular momentum. The state coefficient \(a_n\) is called the amplitude, or sometimes the probability amplitude.

You might be wondering how we would measure that a particle is in a particular state. The answer is to wait for it to jump out. If an atom is excited (for example by a short burst of radiation) it will be excited to a state which is a linear superposition of different energy eigenstates, \(\sum a_n|E_n\rangle\), rather than to a single eigenstate. It will usually return to the ground state by emitting one or a series of photons, and the frequency of an emitted photon reveals the energy difference between the atomic states involved. For a collection of atoms excited in the same way, the relative intensities of different spectral lines give the relative probabilities of different states. Of course, a long almost monochromatic wave packet of incoming radiation will tend to put all the excited atoms into the same state.

Exercise \(\PageIndex{1}\)

Write out the identity operator for the electron in a box \(I=\sum_{n=1}^{\infty} |n\rangle \langle n|\) using the explicit form \(|n\rangle=\sqrt{\frac{2}{L}}\sin \frac{n\pi x}{L}\). Prove this is equivalent to the delta function when operating on other functions within the box. What is the behavior of this function outside the box?

Functions on the Infinite Line

What happens if we take the analysis of the previous section and let \(L\) go to infinity? This is parallel to the analysis (two lectures back) of going from Fourier series to the Fourier transform, the sum over a series of plane waves satisfying a boundary condition becoming an integral over the continuum of all plane waves. In that lecture, we saw that as \(L\) went to infinity, the amplitude of the normalized eigenstates \(|n\rangle\) went to zero as \(1/\sqrt{L}\), and therefore so did the individual coefficients \(a_n=\langle n|\psi\rangle\). However, the density of these eigenstates in momentum space increased as \(L\), so overall the factors of \(L\) cancelled and the sum tended to a finite integral, specifically

\[ \psi(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty} a(k)e^{ikx}dk\]

with

\[a(k)=\int_{-\infty}^{\infty} \psi(x)e^{-ikx}dx \label{2.3.11}\]

For the electron in a box (Fourier series) above we wrote the corresponding equation in Dirac notation as

\[ |\psi(x)\rangle=\sum_{n=1}^{\infty} a_n|n\rangle\]

with

\[a_n=\langle n|\psi\rangle, \; so \; I=\sum_{n=1}^{\infty} |n\rangle \langle n| \label{2.3.12}\]

It’s tempting to write down the analogous equations for the infinite line case, by translating the Fourier transform equations into Dirac notation, and blindly writing \(e^{ikx}=|k\rangle\):

\[ |\psi(x)\rangle=\int_{-\infty}^{\infty} \frac{dk}{2\pi}a(k)|k\rangle, \; a(k)=\int_{-\infty}^{\infty} \psi(x)e^{-ikx}dx=\langle k|\psi(x)\rangle,\; I=\int_{-\infty}^{\infty} \frac{dk}{2\pi} |k\rangle \langle k| \label{2.3.13}\]

This looks good, but has a problem—in contrast to the Fourier series basis functions \(|n\rangle\), these Fourier transform “basis states” \(|k\rangle\) are infinitely long plane wave states \(e^{ikx}\) and therefore not normalizable in the sense we’ve used that term so far. They’re not even in the space we’re supposed to be working in!

Furthermore, \(|\langle k|\psi(x)\rangle|^2\) is not the probability that a measurement of the momentum of the electron will yield precisely the value \(p=\hbar k\). The correct probabilistic interpretation for a continuum of k-values is exactly parallel to the continuum of x-values in ordinary space: \(|\langle k|\psi(x)\rangle|^2dk\) is the probability that a measurement of momentum would find the k-value to be in a small interval of width \(dk\) near \(k\). The probability goes to zero with the width of the interval, and so is vanishingly small if we demand an exact value of \(k\).

But we never measure \(k\) with infinite precision anyway—that would take an infinitely large apparatus. The physically significant quantity is the probability of finding \(k\) in a small interval \(dk\)—in practice, with real detectors, we are always integrating over some (small) range in \(k\).

This means we might be ok with this continuum basis of states: we don’t want them to be normalized in the traditional fashion \(\langle k|k\rangle=1\), because that would correspond to a finite probability of the particle having a mathematically precise value of \(k\), which makes no physical sense—in fact it’s nonsense. The normalization we need is one that makes sense in the context of an integral over a small interval in \(k\)—but still of course over a continuous infinity of basis states!

From our earlier definition of the delta function, we can express orthogonality of these \(|k\rangle\) states: \[ \langle k'|k\rangle=\int_{-\infty}^{\infty} e^{i(k-k')x}dx=2\pi\delta(k-k') \label{2.3.14}\]

and, since the \(\delta\)-function is normalized in the sense that it has total weight one in an integral, we take this equation as the definition of the normalization of the functions \(|k\rangle\). That is to say, we take the state \(|k\rangle\) to have wave function \(Ae^{ikx}\) with \(A=1\).

Now the delta function is only meaningful inside an integral, therefore so is our normalization, and the formalism, a continuum basis of plane wave states with delta function orthogonality, although perhaps leaving something to be desired from a strict mathematical perspective, turns out to be a consistent and reliable way of formulating quantum mechanics.

Exercise \(\PageIndex{1}\)

From the expression for the identity operator above:

\(|\psi\rangle=\int_{-\infty}^{\infty} \frac{dk}{2\pi}|k\rangle\langle k|\psi\rangle\)

substitute \(|k\rangle=e^{ikx}\) and check that this makes sense.

Note: some authors prefer to define the normalized plane wave states by \(|k\rangle=\sqrt{1/2\pi}e^{ikx}\), in which case \(\langle k'|k\rangle=\delta(k'-k)\), and the \(dk/2\pi\) appearing in the above integral for the identity operator becomes simply \(dk\). With our convention, \(dk\) always appears with a \(2\pi\) in the denominator.

Further Note: some prefer to go to a huge, but not infinite box, so the basis momentum eigenstates wave functions are the discrete set \(|k\rangle=\sqrt{\frac{1}{L}}e^{ikx}\), or in three dimensions \(|k\rangle=\sqrt{\frac{1}{V}}e^{i\vec k \cdot \vec x}\), \(V\) being the volume. For this huge box, it is safe to replace the sum over discrete momentum states by an integral, bearing in mind that the density of states in phase space being proportional to \(L\) gives \(\sum_n \equiv\int L\frac{dk}{2\pi}\) or \(\int V\frac{d^3k}{(2\pi)^3}\) in three dimensions. The \(L\) or \(V\) factors finally cancel in computations, as we shall discover later.

Schrödinger’s Equation as an Operator on a Vector Space

As we recounted at the beginning of this course, when Schrödinger was challenged to find a wave equation for the electron wave, he constructed one parallel to the electromagnetic “photon wave equation”, that is to say, he took the energy-momentum equation and wrote

\[E=i\hbar\frac{\partial}{\partial t}, \; p_x=-i\hbar\frac{\partial}{\partial x} \label{2.3.15}\]

He discovered that the three-dimensional version of the differential equation constructed in this way could be solved by standard analytic methods for an electron in an inverse-square force field—the hydrogen atom. The standing wave solutions yielded the right set of energy levels—those Bohr had found earlier with his simplistic model. This confirmed that indeed the wave equation describing the propagation of the electron waves had been discovered, and it was

\[ \left( E-\frac{p^2}{2m}-V(x) \right)\psi(x,t)=0 \label{2.3.16}\]

with \(E,\; p\) the differential operators given above. Since the operator in brackets is linear, the solutions \(\psi(x,t)\) form a linear vector space.

Differential Operators: the Momentum Operator on \(L_2\)

Our task now is to recast this old approach of differential operators acting on wave functions in the equivalent Dirac language. Let’s begin with the simplest, the momentum operator. First, we need to show that it is Hermitian. The trick is to integrate by parts:

\[ \langle \phi|p_x|\psi\rangle=-i\hbar\int_{-\infty}^{\infty}dx \phi^*(x)\frac{d\psi(x)}{dx}=i\hbar\int_{-\infty}^{\infty}dx \psi(x)\frac{d\phi^*(x)}{dx}-[\phi^*(x)\psi(x)]_{-\infty}^{\infty} \label{2.3.17}\]

The last term, the contribution from the infinite endpoints of the integration, must be zero because square-integrable functions must go to zero at infinity, so

\[ \langle \phi|p_x|\psi\rangle=i\hbar\int_{-\infty}^{\infty}dx \psi(x)\frac{d\phi^*(x)}{dx} \label{2.3.18}\]

Now \(p_x|\phi\rangle=-i\hbar d\phi/dx=|p_x\phi\rangle\), so \(\langle p_x\phi|=i\hbar d\phi^*/dx=\langle \phi|p_x^{\dagger}\), and

\[ \langle \phi|p_x|\psi\rangle=i\hbar\int_{-\infty}^{\infty}dx \psi(x)\frac{d\phi^*(x)}{dx}=\langle \phi|p_x^{\dagger}|\psi\rangle \label{2.3.19}\]

we have established that \(p_x=p_x^{\dagger}\) between any two states in the space: so this is an operator identity, and \(p_x=-i\hbar d/dx\) is Hermitian. (The \(i\) is important: the differential operator \(d/dx\) alone is not Hermitian, it’s anti Hermitian in \(L_2\)!

So \(p_x\) is a Hermitian operator, and therefore has real eigenvalues, which it must have since momentum is a physical quantity. But what are its eigenvectors? We already know, of course, that they are the plane wave states—this is the whole reason this particular operator was chosen in building the wave equation in the first place. Strictly speaking, though, as we’ve already discussed, these plane wave states are not in \(L_2\). Nevertheless, any smooth function in \(L_2\) can be expressed as an integral over these states, so they do form a complete basis for the functions relevant to physics.

(It is true that later, in scattering theory and some other places, we may talk about plane waves without always doing an integral: such loose talk should be understood as referring to a very long but finite wave packet, well approximated by a plane wave during the scattering event.)

The Position Operator and Its Eigenstates

The “position” is just the co-ordinate \(x\), manifestly always real, and a Hermitian operator.

Proof:

\[ \langle \varphi|x|\psi\rangle=\int \varphi^*(x)x\psi(x)dx=(\int \psi^*(x)x\varphi(x)dx)^*=\langle \psi|x|\varphi\rangle^*\]

We shall make clear that in this context we regard \(x\) as an operator by writing it with a little hat, \(\hat{x}\). It is equally clear that the eigenstates of \(\hat{x}\), states in which the particle has probability equal to one of being at a particular position, must be delta functions corresponding to that position: that’s the only function with zero probability of finding the particle anywhere else. So if \(|a\rangle\) is an eigenstate of \(x\) with eigenvalue \(a\), \[ |a\rangle=C\delta(x-a) \label{2.3.20}\]

where \(C\) is a constant. But, whatever value we choose for \(C\), this wave function, like the momentum eigenstate, isn’t normalizable—so, in fact, \(|a\rangle\) itself could never be the wave function of a particle!

Example \(\PageIndex{1}\)

Take your favorite definition of the delta function, and prove that it isn’t normalizable, as defined in \(L_2\).

Solution

(It wouldn’t be physically reasonable anyway—to localize a particle to a point would take infinite energy.) But the set of all \(|a\rangle\)’s is certainly complete, and therein lies its value: it is a basis for the space. The convention is to “normalize” these kets, or rather to construct an “orthonormal set”, by analogy with the orthonormalization convention for the plane-wave momentum states, that is, to take

\[ \langle a|b\rangle=\delta(a-b)\]

From the earlier result

\[ \int \delta(a-x)\delta(x-b)dx=\delta(a-b) \]

it follows immediately that \(C=1\).

Therefore,

\[ \langle x|\psi\rangle=\int_{-\infty}^{\infty} dx'\delta(x-x')\psi(x')=\psi(x) \label{2.3.22}\]

Taking the inner product of \(|\psi\rangle\) with the bra \(\langle x|\) just gives the value of \(\psi\)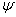 at the point \(x\). Consequently any function \(\psi(x)\) in \(L_2\) can be written:

\[ |\psi\rangle=\int_{-\infty}^{\infty} dx|x\rangle\langle x|\psi\rangle \label{2.3.23}\]

Exercise \(\PageIndex{1}\)

Check that Equation \ref{2.3.23} is true by finding \(\langle x'|\psi\rangle\).

It follows from the Equation \ref{2.3.23} that the identity operator in \(L_2\) can be written in terms of the eigenstates of \(\hat{x}\): \[I=\int_{-\infty}^{\infty} dx|x\rangle \langle x| \label{2.3.24}\]

From this, \(|k\rangle\) can be written \[ |k\rangle=\int_{-\infty}^{\infty} dx|x\rangle\langle x|k\rangle=\int_{-\infty}^{\infty} dxe^{ikx}|x\rangle \label{2.3.25}\]

and \[ |x\rangle=\int_{-\infty}^{\infty} \frac{dk}{2\pi}|k\rangle\langle k|x\rangle=\int_{-\infty}^{\infty} \frac{dk}{2\pi}e^{-ikx}|k\rangle \label{2.3.26}\]

These are possibly the least rigorous equations in this section—we’re expressing one set of states outside of \(L_2\) in terms of another such set, using both sets as bases in \(L_2\)! Obviously, this is only meaningful with an \(|x\rangle\) state defined as a zero-width limit of narrowing Gaussians (say) and a \(|k\rangle\) state as a limit of longer and longer wavepackets, tending to a single k-value. Yet despite the lack of rigor in the above presentation, these states, used with care, are in fact reliable and efficient tools for analyzing quantum mechanical problems. We shall use them often.

Exercise: show these equations are consistent by substituting \(|k\rangle\) from the first into the right-hand side of the second, to give \(|x\rangle=|x\rangle\).

The Hamiltonian Operator

The Hamiltonian operator gives the time development of the wavefunction. It corresponds to the total energy. If the wavefunction corresponds to a definite energy, the time dependence can be factored out, and the spatial wave function is a solution of Schrödinger’s time independent equation: \[ H\psi(x)=\left( \frac{p^2}{2m}+V(x) \right)\psi(x)=-\frac{\hbar^2}{2m}\frac{\partial^2 \psi(x)}{\partial x^2}+V(x)\psi(x)=E\psi(x) \label{2.3.27}\]

_{Since we only consider the space \(L_2\) of wave functions on which both \(p\) and \(x\) are Hermitian, \(H\) must be Hermitian, and therefore has real eigenvalues.}

The Basic Rules of Quantum Mechanics

Any quantum mechanical wave function must be normalizable, because the norm represents the total probability of finding the particle (or, more generally, the system) somewhere in its phase space, so

First Basic Rule: any state of the particle is a ket \(|\psi\rangle\), symbolizing a function \(\psi(x)\) in \(L_2\).

Mathematicians use the term Hilbert space to refer to inner-product spaces of normalizable functions such that any convergent sequence in the space has a limit in the space (a property that, for example, the rational numbers don’t have, but the real numbers do) . Our functions above for the electron in the box do form such a space, with the sine waves an orthonormal basis. However, on going to the infinite line, although we still have normalizable wave functions, the two bases we have discussed above, the plane waves (momentum basis) and the delta functions (position basis)are not themselves in the space—by which we mean they are not normalized as defined in \(L_2\).

But these bases are both complete, meaning any wave function can be expressed in terms of a (continuous) sum over the elements of either of them.

Constructing these complete but not conventionally normalized bases was Dirac’s doing, and is extremely convenient in describing quantum mechanics. But it upset the mathematicians. Fortunately, they later justified it by inventing the theory of distributions, which are generalized functions, and include delta functions.

Bottom Line: we shall follow the other physicists in using the term “Hilbert space” more loosely than mathematicians do, to refer to \(L_2\), extended to include these non-normalizable bases.

Next Basic Rule: A physical variable, or observable, corresponds to a Hermitian operator \(A\) acting on \(L_2\).

We shall assume that the eigenkets of any such variable span the space: this is always true for a finite dimensional space, as previously discussed, but not for a general Hermitian operator in a Hilbert space, so this is a nontrivial assumption.

For an operator with a discrete set of eigenvalues, \(A|n\rangle=\lambda_n|n\rangle\), any wave function can be written \[ |\psi\rangle=\sum c_n|n\rangle,\; with \; c_n=\langle n|\psi\rangle \label{2.3.28}\]

Rule for Relating Operators to Experiments: any measurement of the value of the physical variable \(A\) will yield one of the eigenvalues \(\lambda_n\) of the operator \(A\), and the probability of finding the particular value \(\lambda_n\) is equal to \(|c_n|^2=|\langle n|\psi\rangle|^2\).

The expectation value of an observable \(A\) is the average value of a series of measurements on identical quantum systems, \[ \langle A\rangle=\langle \psi|A|\psi\rangle=\sum |c_n|^2\lambda_n \label{2.3.29}\]

It is important to note that two measurements of the same observable \(A\) on the same system, one measurement being made immediately after the other, must yield the same result. That is to say, if the first measurement reads \(\lambda_n\), the second must be \(\lambda_n\) with 100% probability. But this can only happen if the wave function after the first measurement is \(|n\rangle\), which in general it wasn’t before the first measurement. The jargon description of this is that the act of measurement “collapses the wave function” into one of the eigenstates of the variable being measured.

Measuring a Continuum Variable: For variables like position and momentum having continuum sets of eigenvectors, the statistical interpretation is in terms of finding the particle within some small range—the probability of finding it between \(x\) and \(x+dx\)— is \[ \langle\psi|\int_{x}^{x+dx} dx|x\rangle\langle x|\psi\rangle=\int_{x}^{x+dx} |\psi(x)|^2dx \label{2.3.30}\]

and the expectation value of \(x\) is \[ \langle \psi|x|\psi\rangle=\langle\psi|\hat{x}\int_{-\infty}^{\infty} dx|x\rangle\langle x|\psi\rangle=\int_{-\infty}^{\infty} x|\psi(x)|^2dx \label{2.3.31}\]

where we’ve put a little hat on the \(x\) to remind us that it is an operator, with eigenkets \(|x\rangle\).