9.3: Van Der Waals Forces between Atoms
- Page ID
- 5674
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
The perfect gas equation of state \(PV=NkT\) is manifestly incapable of describing actual gases at low temperatures, since they undergo a discontinuous change of volume and become liquids. In the 1870’s, the Dutch physicist Van der Waals came up with an improvement: a gas law that recognized the molecules interacted with each other. He put in two parameters to mimic this interaction. The first, an attractive intermolecular force at long distances, helps draw the gas together and therefore reduces the necessary outside pressure to contain the gas in a given volume—the gas is a little thinner near the walls. The attractive long range force can be represented by a negative potential \(-aN/V\) on going away from the walls—the molecules near the walls are attracted inwards, those in the bulk are attracted equally in all directions, so effectively the long range attraction is equivalent to a potential well extending throughout the volume, ending close to the walls. Consequently, the gas density \(N/V\) near the walls is decreased by a factor \(e^{-E/kT}=e^{-aN/VkT}\cong 1-aN/VkT\). Therefore, the pressure measured at the containing wall is from slightly diluted gas, so \(P=(N/V)kT\) becomes \(P=(N/V)(1-aN/VkT)kT\), or \((P+a(N/V)^2)V=NkT\). The second parameter van der Waals added was to take account of the finite molecular volume. A real gas cannot be compressed indefinitely—it becomes a liquid, for all practical purposes incompressible. He represented this by replacing the volume \(V\) with \(V-Nb\), \(Nb\) is referred to as the “excluded volume”, roughly speaking the volume of the molecules. Putting in these two terms gives his famous equation \[ \left[ P+a\left(\frac{N}{V}\right)^2\right] (V-Nb)=NkT. \label{9.3.1}\]
This rather crude approximation does in fact give sets of isotherms representing the basic physics of a phase transition quite well. (For further details, and an enlightening discussion, see for example Appendix D of Thermal Physics, by R. Baierlein.)
Ground State Hydrogen Atoms
Our interest here is in understanding the van der Waals long-range attractive force between electrically neutral atoms and molecules in quantum mechanical terms. We begin with the simplest possible example, two hydrogen atoms, both in the ground state:
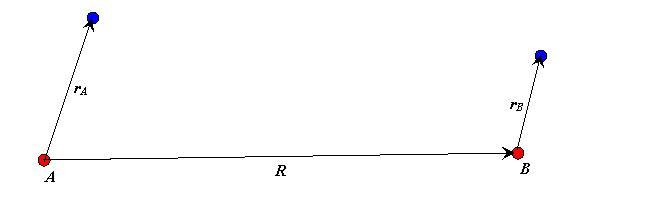
We label the atoms \(A\) and \(B\), the vectors from the protons to the electron position are denoted by \(\vec{r_A}\) and \(\vec{r_B}\) respectively, and \(\vec{R}\) is the vector from proton \(A\) to proton \(B\).
Then the Hamiltonian \(H=H^0+V\), where \[ H^0=-\frac{\hbar^2}{2m}(\nabla^2_A+\nabla^2_B)-\frac{e^2}{r_A}-\frac{e^2}{r_B} \label{9.3.2}\]
and the electrostatic interaction between the two atoms \[ V=\frac{e^2}{R}+\frac{e^2}{|\vec{R}+\vec{r_B}-\vec{r_A}|}-\frac{e^2}{|\vec{R}+\vec{r_B}|}-\frac{e^2}{|\vec{R}-\vec{r_A}|} \label{9.3.3}\]
The ground state of \(H^0\) is just the product of the ground states of the atoms \(A,B\), that is, \[ |0\rangle =|100\rangle_A\otimes |100\rangle_B. \label{9.3.4}\]
Assuming now that the distance between the two atoms is much greater than their size, we can expand the interaction \(V\) in the small parameters \(r_A/R,\; r_B/R\). As one might suspect from the diagram above, the leading order terms in the electrostatic energy are just those of a dipole-dipole interaction: \[ V=-e^2(\vec{r_A}\cdot \vec{\nabla})(\vec{r_B}\cdot \vec{\nabla})\frac{1}{R}=e^2\left[ \frac{\vec{r_A}\cdot \vec{r_B}}{R^3}-\frac{3(\vec{r_A}\cdot \vec{R})(\vec{r_B}\cdot \vec{R})}{R^5}\right] \label{9.3.5}\]
Taking now the z- axis in the direction \(\vec{R}\), this interaction energy is \[ V=\frac{e^2}{R^3}(x_Ax_B+y_Ay_B-2z_AZ_B) \label{9.3.6}\]
Now the first-order correction to the ground state energy of the two-atom system from this interaction is \(E^1_n=\langle n^0|H^1|n^0\rangle\), where here \(H^1=V\) and \(|n^0\rangle =|100\rangle_A\otimes |100\rangle_B\). Beginning with the first term \(x_Ax_B\) in \(V\) \[ (_A\langle 100|\otimes_B\langle 100|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle 100|x_A|100\rangle_A)(_B\langle 100|x_B|100\rangle_B) \label{9.3.7}\]
is clearly zero since the ground states are spherically symmetric. Similarly, the other terms in \(V\) are zero to first order.
Recall that the second-order energy correction is \(E^2_n=\sum_{m\neq n} \frac{|\langle m0|H^1|n^0\rangle |^2}{E^0_n-E^0_m} \).
That is, \[ E^{(2)}=\sum_{\begin{matrix}n,l,m\\ n′,l′,m′ \end{matrix}} \frac{|(_A\langle nlm|\otimes_B\langle n′l′m′|)V(|100\rangle_A\otimes |100\rangle_B)|^2}{2E_1-E_n-E_{n′}}. \label{9.3.8}\]
A typical term here is \[ (_A\langle nlm|\otimes_B\langle n′l′m′|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle nlm|x_A|100\rangle_A)(_B\langle n′l′m′|x_B|100\rangle_B), \label{9.3.9}\]
so the single-atom matrix elements are exactly those we discussed for the Stark effect (as we would expect—this is an electrostatic interaction!). As before, only \(l=1,\;\; l′=1\) contribute. To make a rough estimate of the size of \(E^{(2)}\), we can use the same trick used for the quadratic Stark effect: replace the denominators by the constant \(2E_1\) (the other terms are a lot smaller for the bound states, and continuum states have small overlap terms in the numerator). The sum over intermediate states \(n,l,m,n′,l′,m′\) can then be taken to be completely unrestricted, including even the ground state, giving \[ \sum_{\begin{matrix}n,l,m\\ n′,l′,m′ \end{matrix}} (|nlm\rangle_A\otimes |n′l′m′\rangle_B)(_A\langle nlm|\otimes_B\langle n′l′m′|)=I, \label{9.3.10}\]
the identity operator. In this approximation, then, just as for the Stark effect, \[ E^{(2)}\simeq \frac{e^4}{R^6}\frac{1}{2E_1}(_A\langle 100|\otimes_B\langle 100|)(x_Ax_B+y_Ay_B-2z_AZ_B)^2(|100\rangle_A\otimes |100\rangle_B) \label{9.3.11}\]
where \(E_1=-1\) Ryd., so this is a lowering of energy.
In multiplying out \((x_Ax_B+y_Ay_B-2z_AZ_B)^2\), the cross terms will have expectation values of zero. The ground state wave function is symmetrical, so all we need is \(\langle 100|x^2|100\rangle =a^2_0\), where \(a_0\) is the Bohr radius.
This gives
\[ E^{(2)}\simeq \frac{e^4}{R^6}\frac{1}{2E_1}6a^4_0\simeq -6\frac{e^2}{R}\left( \frac{a_0}{R}\right)^5 \label{9.3.12}\]
using \(E_1=-e^2/2a_0\). Bear in mind that this is an approximation, but a pretty good one—a more accurate calculation replaces the 6 by 6.5.
Forces between a 1s Hydrogen Atom and a 2p Hydrogen Atom
With one atom in the \(|100\rangle\) and the other in \(|210\rangle\), say, a typical leading order term would be
\[ (_A\langle 100|\otimes_B\langle 210|)(x_Ax_B)(|100\rangle_A\otimes |100\rangle_B)=(_A\langle 100|x_A|100\rangle_A)(_B\langle 210|x_B|100\rangle_B), \label{9.3.13}\]
and this is certainly zero, as are all the other leading terms. Baym (Lectures on Quantum Mechanics) concluded from this that there is no leading order energy correction between two hydrogen atoms if one of them is in the ground state. This is incorrect: the first excited state of the two-atom system (without interaction) is degenerate, so, exactly as for the 2-D simple harmonic oscillator treated in the previous lecture, we must diagonalize the perturbation in the subspace of these degenerate first excited states. (For this section, we follow fairly closely the excellent treatment in Quantum Mechanics, by C. Cohen-Tannoudji et al.)
The space of the degenerate first excited states of the two noninteracting atoms is spanned by the product-space kets: \[ \begin{matrix} (|100\rangle_A\otimes |200\rangle_B), &(|200\rangle_A\otimes |100\rangle_B),&(|100\rangle_A\otimes |211\rangle_B),&(|211\rangle_A\otimes |100\rangle_B),\\ (|100\rangle_A\otimes |210\rangle_B),&(|210\rangle_A\otimes |100\rangle_B),&(|100\rangle_A\otimes |21-1\rangle_B),&(|21-1\rangle_A\otimes |100\rangle_B). \end{matrix} \label{9.3.14}\]
The task, then, is to diagonalize \(V=\frac{e^2}{R^3}(x_Ax_B+y_Ay_B-2z_AZ_B)\) in this eight-dimensional subspace.
We begin by representing \(V\) as an \(8\times 8\) matrix using these states as the basis. First, note that all the diagonal elements of the matrix are zero—in all of them, we’re finding the average of x,y or z for one of the atoms in the ground state. Second, writing \(V=\frac{e^2}{R^3}(\vec{r_A}\cdot \vec{r_B}-3z_AZ_B)\), it is evident that \(V\) is unchanged if the system is rotated around the z- axis (the line joining the two protons). This means that the commutator \([V,L_z]=0\), where \(L_z\) is the total angular momentum component in the z- direction, so \(V\) will only have nonzero matrix elements between states having the same total \(L_z\). Third, from parity (or Wigner-Eckart) all matrix elements in the subspace spanned by \((|100\rangle_A\otimes |200\rangle_B),\; (|200\rangle_A\otimes |100\rangle_B)\) must be zero.
This reduces the nonzero part of the \(8\times 8\) matrix to a direct product of three \(2\times 2\) matrices, corresponding to the three values of \(L_z=m\). For example, the \(m=0\) subspace is spanned by \((|100\rangle_A\otimes |210\rangle_B),\; (|210\rangle_A\otimes |100\rangle_B)\). The diagonal elements of the \(2\times 2\) matrix are zero, the off-diagonal elements are equal to \(-2\frac{e^2}{R^3}(_A\langle 100|z_A|210\rangle_A)(_B\langle 210|Z_B|100\rangle_B)\), where we have kept the unnecessary labels \(A,B\) to make clear where this term comes from. (The \(x_A\) and \(y_A\) terms will not contribute for \(m=0\). )
This is now a straightforward integral over hydrogen wave functions. The three \(2\times 2\) matrices have the form \[ \begin{pmatrix} 0&k_m/R^3\\ k_m/R^3 &0 \end{pmatrix} \label{9.3.15}\]
(following the notation of Cohen-Tannoudji) where \(k_m\sim e^2a^2_0\), and the energy eigenvalues are \(\pm k_m/R^3\), with corresponding eigenkets \( (1/\sqrt{2})[(|100\rangle_A\otimes |210\rangle_B)\pm (|210\rangle_A\otimes |100\rangle_B)]\).
So for two hydrogen atoms, one in the ground state and one in the first excited state, the van der Waal interaction energy goes as \(1/R^3\), much more important than the \(1/R^6\) energy for two hydrogen atoms in the ground state. Notice also that the \(1/R^3\) can be positive or negative, depending on whether the atoms are in an even or an odd state—so the atoms sometimes repel each other.
Finally, if two atoms are initially in a state \((|100\rangle_A\otimes |210\rangle_B)\), note that this is not an eigenstate of the Hamiltonian when the interaction is included. Writing the state as a sum of the even and odd states, which have slightly different phase frequencies from the energy difference, we find the excitation moves back and forth between the two atoms with a period \(hR^3/2k_{m=0}\).


