11.9: Problems
- Page ID
- 89963
11.9.1 a super-speed super?
Take two more steps in the parable of the Great Betrayal (Box 11.1).
a. Find the speed of a new rocket frame moving relative to the Klingon frame such that the Super travels at 6 times the speed of light in this new frame. Hint: Examine the coordinates \(x^{\prime}\) and \(t^{\prime}\) of event 3 in the new frame. The ratio of these two, \(x^{\prime} / t^{\prime}\), is the speed of the Super in this frame. We know the coordinates of event 3 in the Klingon frame. Therefore
b. Find the speed of yet another rocket frame, relative to the Klingon frame, such that the Super travels with infinite speed in this frame. Hint: What does infinite speed imply about the time \(t^{\prime}\) between events 0 and 3 in this new frame?
11.9.2 a bad clock
Note: This exercise uses spacetime diagrams, introduced in Chapter 5 .
A pulse of light is reflected back and forth between mirrors \(A\) and \(B\) separated by 2 meters of distance in the \(x\)-direction in the Earth frame, as shown in the figure (left). A swindler tells us that this device constitutes a clock that "ticks" every time the pulse arrives at either mirror.
The swindler claims that events 1 through 6 are sequential "ticks" of this clock (center). However, we notice that the ticking of the clock is uneven in a rocket frame moving with speed \(v_{\text {rel }}\) in the Earth frame (right). For example, there is less time between events 0 and 1 than between events 1 and 2 as measured in the rocket frame.
a. What is the physical basis for the "bad" behavior of this clock? Use the Lorentz transformation



b Use some of the same events 0 through 4 to define a "good" clock that ticks evenly in both the laboratory frame and the rocket frame. From the spacetime diagrams, show qualitatively that your good clock "runs slow" as observed from the rocket frame - as it must, since the clock is in motion with respect to the rocket frame.
c Explain why the clock of Figure 1-3 in the text is a "good" clock.
11.9.3 the Galilean transformation
a Use everyday, nonrelativistic Newtonian arguments to derive transformation equations between reference frames moving at low relative velocities. Show that the result is
\[\begin{aligned} x^{\prime}=x-v_{\text {conv }} t_{\text {sec }} & \text { (Newtonian: } v_{\text {conv }}<<c \text { ) } \\ t_{\text {sec }}^{\prime}=t_{\text {sec }} \quad \text { (Newtonian: } v_{\text {conv }}<<c \text { ) } \end{aligned}\]
where \(t_{\text {sec }}\) is time measured in seconds and \(v_{\text {conv }}\) is speed in conventional units (meters/second for example). List the assumptions you make in your derivation.
b Convert equations (1) and (2) to measure time \(t\) in meters and unitless measure of relative velocity, \(v_{\mathrm{rel}}=v_{\mathrm{con}} / c\). Show the results are:
\[\begin{aligned} x^{\prime}=x-v_{\text {rel }} t &(\text { Newtonian: } v<<1) \\ t^{\prime}=t &(\text { Newtonian: } v<<1) \end{aligned}\]
Do the new units make these equations correct at high relative velocity between frames?
c Use the first two terms in the binomial expansion to find a low-velocity approximation for \(\gamma\) in the Lorentz transformation.
\[\gamma=\frac{1}{\left(1-v_{\mathrm{rel}}^{2}\right)^{1 / 2}}=\left(1-v_{\mathrm{rel}}^{2}\right)^{-1 / 2} \approx 1+\frac{v_{\mathrm{rel}}^{2}}{2} \nonumber \]
Show that this expression differs from unity by less than one percent provided \(v\) is less than \(1 / 7\). A sports car can accelerate uniformly from rest to 60 miles / hour (about 27 meters/second) in 7 seconds. Roughly how many days would it take for the sports car to reach \(v=1 / 7\) at the same constant acceleration?
d \(\operatorname{Set} \gamma=1\) in the Lorentz transformation equations. Show that the resulting "low-velocity Lorentz transformation" is
\[\begin{array}{cc} x^{\prime}=x-v_{\text {rel }} t \quad & \text { (Lorentz: } v<<1 \text { ) } \\ t^{\prime}=-v_{\text {rel }} x+t \quad \text { (Lorentz: } v<<1 \text { ) } \end{array}\]
What is the difference between the time transformations for the "Newtonian low-velocity limit" of equation (4) and the "Lorentz low-velocity limit" of equation (6)? How can they both be correct? The term - \(v_{\text {rel }} x\) does not depend on any time lapse, but only on the separation \(x\) of the event from the laboratory origin. This term is due to the difference of synchronization of clocks in the two frames.
e In each of the following cases a laboratory clock (measuring \(t\) ) at a distance \(x\) from the origin as measured in the laboratory frame is compared with a passing rocket clock (measuring \(t^{\prime}\) ). Say whether or not the time difference \(t-t^{\prime}=v_{\text {rel }} x\) can be detected using wristwatches (accuracy of \(10^{-1}\) second \(=3 \times\) \(10^{7}\) meters of light-travel time) and using modern electronic clocks (accuracy of \(10^{-9}\) second \(=0.3\) meter of time).
(1) Sports car traveling at 100 kilometers/hour (roughly 30 meters/second) located 1000 kilometers down the road from the origin as measured in the Earth frame.
(2) Moon probe traveling at 30,000 kilometers hour passing Moon, \(3.8 \times 10^{5}\) kilometers from the origin on Earth as measured in the Earth frame.
(3) Distance from origin on Earth at which space probe traveling at 30,000 kilometers/hour leads to detectable time difference between rocket wristwatch and adjacent Earth-linked latticework clock. Compare with Earth - Sun distance of \(1.5 \times 10^{11}\) meters
\(\mathbf{f}\) Summarize in a sentence or two the conditions under which the regular Galilean transformation equations (3) and (4) will lead to correct predictions.
11.9.4 limits of Newtonian
Use the particle speed \(v_{\text {crit }}=1 / 7\) (Exercise 11.7.3 as an approximate maximum limit for the validity of Newtonian mechanics. Determine whether or not Newtonian mechanics is adequate to analyze motion in each of the following cases, following the example.
Example: Satellite circling Earth at 30,000 kilometers/hour \(=18,000\) miles/hour. Answer: Light moves at a speed \(v_{\text {conv }}=\left(3 \times 10^{5}\right.\) kilometers \(/\) second) \(\times(3600 \quad\) seconds \(/\) hour \()=1.08 \times 10^{9}\) kilometers/hour. Therefore the speed of the satellite in meters/meter is \(v=v_{\text {conv }} / c=2.8 \times 10^{-5}\). This is much less than \(v_{\text {cit }}=1 / 7\), so the Newtonian description of satellite motion is adequate.
a Earth circling Sun at an orbital speed of 30 kilometers/second.
b Electron circling a proton in the orbit of smallest radius in a hydrogen atom. Discussion: The classical speed of the electron in the inner orbit of an atom of atomic number \(Z\), where \(Z\) is the number of protons in the nucleus, is given, for low velocities, by the expression \(v=Z / 137\). For hydrogen, \(Z=1\).
c Electron in the inner orbit of the gold atom, for which \(Z=79\).
d Electron after acceleration from rest through a voltage of 5000 volts in a black-and-white television picture tube. Discussion: We say that this electron has a kinetic energy of 5000 electron-volts. One electron-volt is equal to \(1.6 \times 10^{-19}\) joule. Try using the Newtonian expression for kinetic energy.
- Electron after acceleration from rest through a voltage of 25,000 volts in a color television picture tube.
f A proton or neutron moving with a kinetic energy of \(10 \mathrm{MeV}\) (million electron-volts) in a nucleus.
11.9.5 Doppler shift
A sparkplug at rest in the rocket emits light with a frequency \(f^{\prime}\) pulses or waves per second. What is the frequency \(f\) of this light as observed in the laboratory? Let this train of waves (or pulses) of light travel in the positive \(x\)-direction with speed \(c\), so that in the course of one meter of light-travel time, \(f / c\) of these pulses pass the origin of the laboratory frame. It is understood that the zeroth or "fiducial"’ crest or pulse passes the origin at the zero of time-and that the origin of the rocket frame passes the origin of the laboratory frame at this same time.
a Show that the \(x\)-coordinate of the \(n\)th pulse or wave crest is related to the time of observation \(t\) (in meters) by the equation
\[n=(f / c)(t-x)\]
\(\mathbf{b}\) The same argument, applied in the rocket frame, leads to the relation
\[n=\left(f^{\prime} / c\right)\left(t^{\prime}-x^{\prime}\right)\]
Express this rocket formula in laboratory coordinates \(x\) and \(t\) using the Lorentz transformation. Equate the resulting expression for \(f^{\prime}\) to the laboratory formula for \(f\) in terms of \(x\) and \(t\) to derive the simple formula for \(f\) in terms of \(f^{\prime}\) and \(v_{\text {rel }}\), the relative speed of laboratory and rocket frames.
\[f=\left(\frac{1+v_{\mathrm{rel}}}{1-v_{\mathrm{rel}}}\right)^{1 / 2} f^{\prime}\] [wave moves in positive \(\mathrm{x}\)-direction]
c Now observe a wave moving along the negative \(x\)-direction from the same source at rest in the rocket frame. Show that the frequency of the wave observed in the laboratory frame is
\[f=\left(\frac{1-v_{\text {rel }}}{1+v_{\text {rel }}}\right)^{1 / 2} f^{\prime} \quad \begin{array}{r} \text { [wave moves in } \\ \text { negative } \mathbf{x} \text {-direction] } \end{array}\]
d Astronomers define the redshift \(z\) of light from a receding astronomical object by the formula
\[z=\frac{f_{\mathrm{emit}}-f_{\mathrm{obs}}}{f_{\mathrm{obs}}}\]
Here \(f_{\text {emit }}\) is the frequency of the light measured in the frame in which the emitter is at rest and \(f_{\text {obs }}\) the frequency observed in another frame in which the emitter moves directly away from the observer.
The most distant quasar reported as of 1991 has a redshift \(z=4.897\). With what fraction of the speed of light is this quasar receding from us?
Reference: D. P. Schneider, M. Schmidt, and J. E. Gunn, Astronomical Journal, Volume 102, pages \(837-840\) (1991).
11.9.6 transformation of angles
a A meter stick lies at rest in the rocket frame and makes an angle \(\phi^{\prime}\) with the \(x^{\prime}\)-axis. Laboratory observers measure the \(x\)-and \(y\)-projections of the stick as it streaks past. What values do they measure for these projections, compared with the \(x^{\prime}\) - and \(y^{\prime}\)-projections measured by rocket observers? Therefore what angle \(\phi\) does the same meter stick make with the \(x\)-axis of the laboratory frame? What is the length of the "meter stick" as observed in the laboratory frame?
b Make the courageous assumption that the directions of electric-field lines around a point charge transform in the same way as the directions of meter sticks that lie along these lines. (Electric field lines around a point charge are assumed to be infinite in length, so the length transformation of part a does not apply.) Draw qualitatively the electric-field lines due to an isolated positive point charge at rest in the rocket frame as observed in (1) the rocket frame and (2) the laboratory frame. What conclusions follow concerning the time variation of electric forces on nearby charges at rest in the laboratory frame?
11.9.7 transformation of \(y\)-velocity
A particle moves with uniform speed \(v_{y}^{\prime}=\Delta y^{\prime} / \Delta t^{\prime}\) along the \(y^{\prime}\)-axis of the rocket frame. Transform \(\Delta y^{\prime}\) and \(\Delta t^{\prime}\) to laboratory displacements \(\Delta x, \Delta y\), and \(\Delta t\) using the Lorentz transformation equations. Show that the \(x\)-component and the \(y\)-component of the velocity of this particle in the laboratory frame are given by the expressions \[\begin{aligned} &v_{x}=v_{\mathrm{rel}} \\ &v_{y}=v_{y}^{\prime}\left(1-v_{\mathrm{rel}}^{2}\right)^{1 / 2} \end{aligned}\]
11.9.8 transformation of velocity direction
A particle moves with velocity \(v^{\prime}\) in the \(x^{\prime} y^{\prime}\) plane of the rocket frame in a direction that makes an angle \(\phi^{\prime}\) with the \(x^{\prime}\)-axis. Find the angle \(\phi\) that the velocity vector of this particle makes with the \(x\)-axis of the laboratory frame. (Hint: Transform space and time displacements rather than velocities.) Why does this angle differ from that found in Exercise L-6 on transformation of angles? Contrast the two results when the relative velocity between the rocket and laboratory frames is very great.
11.9.9 the headlight effect
A flash of light is emitted at an angle \(\phi^{\prime}\) with respect to the \(x^{\prime}\)-axis of the rocket frame.a Show that the angle \(\phi\) the direction of motion of this flash makes with respect to the \(x\)-axis of the laboratory frame is given by the equation
\[\cos \phi=\frac{\cos \phi^{\prime}+v_{\mathrm{rel}}}{1+v_{\mathrm{rel}} \cos \phi^{\prime}} \nonumber \]
b Show that your answer to Exercise L-8 gives the same result when the velocity \(v^{\prime}\) is given the value unity.
c A particle at rest in the rocket frame emits light uniformly in all directions. Consider the 50 percent of this light that goes into the forward hemisphere in the rocket frame. Show that in the laboratory frame this light is concentrated in a narrow forward cone of half-angle \(\phi_{0}\) whose axis lies along the direction of motion of the particle. The half-angle \(\phi_{0}\) is the solution to the following equation:
\[\cos \phi_{\mathrm{o}}=v_{\mathrm{rel}} \nonumber \]
This result is called the headlight effect.
11.9.10 the tilted meter stick

Note: This exercise uses the results of Exercise L-7.
A meter stick lying parallel to the \(x\)-axis moves in the \(y\)-direction in the laboratory frame with speed \(v_{y}\) as shown in the figure (left).
a In the rocket frame the stick is tilted upward in the positive \(x^{\prime}\)-direction as shown in the figure (right). Explain why this is, first without using equations. \(\mathbf{b}\) Let the center of the meter stick pass the point \(x=y=x^{\prime}=y^{\prime}=0\) at time \(t=t^{\prime}=0\). Calculate the angle \(\phi^{\prime}\) at which the meter stick is inclined to the \(x^{\prime}\)-axis as observed in the rocket frame. Discussion: Where and when does the right end of the meter stick cross the \(x\)-axis as observed in the laboratory frame? Where and when does this event of right-end crossing occur as measured in the rocket frame? What is the direction and magnitude of the velocity of the meter stick in the rocket frame (Exercise L-7)? Therefore where is the right end of the meter stick at \(t^{\prime}=0\), when the center is at the origin? Therefore ..
11.9.11 the rising manhole
Note: This exercise uses the results of Exercise L-10.

A meter stick lies along the \(x\)-axis of the laboratory frame and approaches the origin with velocity \(v_{\text {rel }}\). A very thin plate parallel to the \(x z\) laboratory plane moves upward in the \(y\)-direction with speed \(v_{y}\) as shown in the figure. The plate has a circular hole with a diameter of one meter centered on the \(y\)-axis. The center of the meter stick arrives at the laboratory origin at the same time in the laboratory frame as the rising plate arrives at the plane \(y=0\). Since the meter stick is Lorentz-contracted in the laboratory frame it will easily pass through the hole in the rising plate. Therefore there will be no collision between meter stick and plate as each continues its motion. However, someone who objects to this conclusion can make the following argument: "In the rocket frame in which the meter stick is at rest the meter stick is not contracted, while in this frame the hole in the plate is Lorentz-contracted. Hence the full-length meter stick cannot possibly pass through the contracted hole in the plate. Therefore there must be a collision between the meter stick and the plate." Resolve this paradox using your answer to Exercise \(\mathrm{L}-10\). Answer unequivocally the question, Will there be a collision between the meter stick and the plate?
Reference: \(R\). Shaw, American Journal of Pbysics, Volume 30, page 72 (1962).
11.9.12 paradox of the skateboard and the grid
A girl on a skateboard moves very fast, so fast that the relativistic length contraction makes the skateboard very short. On the sidewalk she has to pass over a grid. A man standing at the grid fully expects the fast short skateboard to fall through the holes in the grid. Yet to the fast girl her skateboard has its usual length and it is the grid that has the relativistic contraction. To her the holes in the grid are much narrower than to the stationary man, and she certainly does not expect her skateboard to fall through them. Which person is correct? The answer hinges on the relativity of rigidity.
Idealize the problem as a one-meter rod sliding lengthwise over a flat table. In its path is a hole one meter wide. If the Lorentz contraction factor is ten, then in the table (laboratory) frame the rod is 10 centimeters long and will easily drop into the onemeter-wide hole. Assume that in the laboratory frame the meter stick moves fast enough so that it remains essentially horizontal as it descends into the hole (no "tipping" in the laboratory frame). Write an equation in the laboratory frame for the motion of the bottom edge of the meter stick assuming that \(t=\) \(t^{\prime}=0\) at the instant that the back end of the meter stick leaves the edge of the hole. For small vertical velocities the rod will fall with the usual acceleration \(g\). Note that in the laboratory frame we have assumed that every point along the length of the meter stick begins to fall simultaneously.
In the meter stick (rocket) frame the rod is one meter long whereas the hole is Lorentz-contracted to a 10 -centimeter width so that the rod cannot possibly fit into the hole. Moreover, in the rocket frame different parts along the length of the meter stick begin to drop at different times, due to the relativity of simultaneity. Transform the laboratory equations into the rocket frame. Show that the front and back of the rod will begin to descend at different times in this frame. The rod will "droop" over the edge of the hole in the rocket frame - that is, it will not be rigid. Will the rod ultimately descend into the hole in both frames? Is the rod really rigid or nonrigid during the experiment? Is it possible to derive any physical characteristics of the rod (for example its flexibility or compressibility) from the description of its motion provided by relativity?
11.9.13 paradox of the identically accelerated twins
Note: This exercise uses spacetime diagrams, introduced in Chapter \(5 .\)
Two fraternal twins, Dick and Jane, own identical spaceships each containing the same amount of fuel. Jane’s ship is initially positioned a distance to the right of Dick’s in the Earth frame. On their twentieth birchday they blast off at the same instant in the Earth frame and undergo identical accelerations to the right as measured by Mom and Dad, who remain at home on Earth. Mom and Dad further observe that the twins run out of fuel at the same time and move thereafter at the same speed \(v\). Mom and Dad also measure the distance between Dick and Jane to be the same at the end of the trip as at the beginning.
Dick and Jane compare the ships’ logs of their accelerations and find the entries to be identical. However when both have ceased accelerating, Dick and Jane, in their new rest frame, discover that Jane is older than Dick! How can this be, since they have an identical history of accelerations?
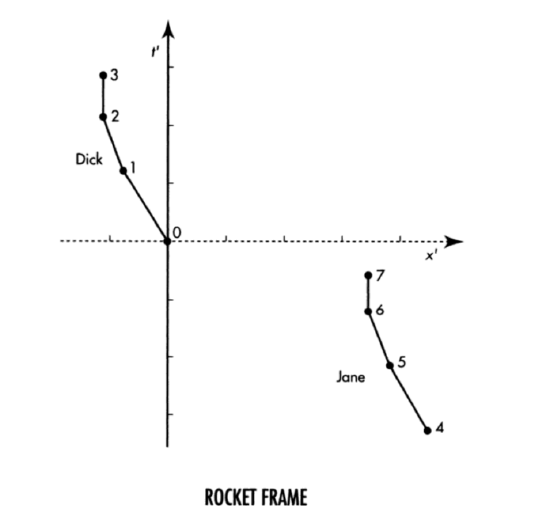
a Analyze a simpler trip, in which each spaceship increases speed not continuously but by impulses, as shown in the first spacetime diagram and the event table. How far apart are Dick and Jane at the beginning of their trip, as observed in the Earth frame? How far apart are they at the end of their accelerations? What is the final speed \(v\) (not the average speed) of the two spaceships? How much does each astronaut age along the worldline shown in the diagram? (The answer is not the Earth time of 12 years.)
b The second spacetime diagram shows the two worldlines as recorded in a rocket frame moving with the final velocity of the two astronauts. Copy the figure. On your copy extend the worldlines of Dick and Jane after each has ceased accelerating. Label your figure to show that Jane ceased accelerating before Dick as observed in this frame. Will Dick age the same between events 0 and 3 in this frame as he aged in the Earth frame? Will Jane age the same between events 4 and 7 in this frame as she aged in the Earth frame?
c Now use the Lorentz transformation to find the space and time coordinates of one or two critical events in this final rest frame of the twins in order to answer the following questions
(1) How many years earlier than Dick did Jane cease accelerating?
(2) What is Dick’s age at event 3? (not the rocket time \(t^{\prime}\) of this event!) (3) What is Jane’s age at event 7 ?
(4) What is Jane’s age at the same time (in this frame) as event 3?
(5) What are the ages of Dick and Jane 20 years after event 3 , assuming that neither moves again with respect to this frame?
(6) How far apart in space are Dick and Jane when both have ceased accelerating?
(7) Compare this separation with their initial (and final!) separation measured by Mom and Dad in the Earth frame
d Extend your results to the general case in which Mom and Dad on Earth observe a period of identical continuous accelerations of the two twins.
(1) At the two start-acceleration events (the two events at which the twins start their rockets), the twins are the same age as observed in the Earth frame. Are they the same age at these events as observed in every rocket frame?
(2) At the two cease-acceleration events (the two events at which the rockets run out of fuel), are the twins the same age as observed in the Earth frame? Are they the same age at these events as observed in every rocket frame?
(3) The two cease-acceleration events are simultaneous in the Earth frame. Are they simultaneous as observed in every rocket frame? (No!) Whose cease-acceleration event occurs first as observed in the final frame in which both twins come to rest? (Recall the Train Paradox, Section 3.4.)
(4) "When Dick ceases accelerating, Jane is older than Dick." Is this statement true according to the astronauts in their final rest frame? Is the statement true according to Mom and Dad in the Earth frame?
(5) Criticize the lack of clarity (swindle?) of the word \(w h e n\) in the statement of the problem: "However when both have ceased accelerating, Dick and Jane, in their new rest frame, discover that Jane is older than Dick!"
e Suppose that Dick and Jane both accelerate to the left, so that Dick is in front of Jane, but their history is otherwise the same. Describe the outcome of this trip and compare it with the outcome of the original trip.
f Suppose that Dick and Jane both accelerate in a direction perpendicular to the direction of their separation. Describe the outcome of this trip and compare it with the outcome of the original trip.

Discussion: Einstein postulated that physics in a uniform gravitational field is, locally and for small particle speeds, the same as physics in an accelerated frame of reference. In this exercise we have found that two accelerated clocks separated along the direction of acceleration do not remain in synchronism as observed simultaneously in their common frame. Rather, the forward clock reads a later time ("runs faster") than the rearward clock as so observed. Conclusion from Einstein’s postulate: Two clocks one above the other in a uniform gravitational field do not remain in synchronism; rather the higher clock reads a later time ("runs faster") than the lower clock. General relativity also predicts this result, and experiment verifies it. (Read about the patrol plane experiment in Section 4.10.)
Reference: S. P. Boughn, American Journal of Pbysics, Volume 57 , pages \(791-793\) (September 1989), Reference to general relativity result: Wolfgang Rindler, Essential Relativity (Springer, New York, 1977 ), pages 17 and 117 .
11.9.14 how do rods Lorentz- contract?
Note: Calculus is used in the solution to this exercise; so is the formula for Lorentz contraction from Section \(5.8\).
Laboratory observers measure the length of a moving rod lying along its direction of motion in the laboratory frame. Then the rod speeds up a little. Again laboratory observers measure its length, which they find to be a little shorter than before. They call this shortening of length Lorentz contraction. How did this shortening of length come about? As happens so often in relativity, the answer lies in the relativity of simultaneity.
First, how much shortening takes place when the rod changes from speed \(v\) to speed \(v+d v\) ? Let \(L_{\mathrm{o}}\) be the proper length of the rod when measured at rest. At speed \(v\) its laboratory-measured length \(L\) will be shorter than this by the Lorentz contraction factor (Section 5.8):
\[L=\left(1-v^{2}\right)^{1 / 2} L_{o} \nonumber \]
a Using calculus, show that when the rod speeds up from \(v\) to a slightly greater speed \(v+d v\), the change in length \(d L\) is given by the expression
\[d L=-\frac{L_{\mathrm{o}} v d v}{\left(1-v^{2}\right)^{1 / 2}} \nonumber \]
The negative sign means that the change is a shortening of the rod. We want to explain this change in length.
How is the rod to be accelerated from \(v\) to \(v+d v\) ? Fire a rocket attached to the rear of the rod? No. Why not? Because the rocket pushes only against the rear of the rod; this push is transmitted along the rod to the front at the speed of a compression wave - very slow! We want the front and back to change speed "at the same time" (exact meaning of this phrase to be determined later). How can this be done? Only by prearrangement! Saw the rod into a thousand equal pieces and tap each piece in the forward direction with a mallet "at exactly 12 noon" as read off a set of synchronized clocks. To simplify things for now, set aside all but the front and back pieces of the rod. Now tap the front and back pieces "at the same time." The change in length of the rod \(d L\) is then the change in distance between these two pieces as a result of the tapping. So much for how to accelerate the "rod."
Now the central question: What does it mean to tap the front and back pieces of the rod "at the same time"? To answer this question, ask another: What is our final goal? Answer: To account for the Lorentz contraction of a fast-moving rod of proper length \(L_{0}\). More: We want a careful inspector riding on the fast-moving rod to certify that it has the same proper length \(L_{0}\) as it did when it was at rest in the laboratory frame. To achieve this goal, the inspector insists that the pair of accelerating taps be applied to the front and back rod pieces at the same time in the current rest frame of the rod. Otherwise the distance between these pieces would not remain the same in the frame of the rod; the rod would change proper length. [Notice that in Exercise L-13 the taps occur at the same time in the laboratory (Earth) frame. This leads to results different from those of the present exercise.]
b You are the inspector riding along with the front and back pieces of the rod. Consider the two events of tapping the front and back pieces. How far apart \(\Delta x^{\prime}\) are these events along the \(x\)-axis in your (rocket) frame? How far apart \(\Delta t^{\prime}\) in time are these events in your frame? Predict how far apart in time \(\Delta t\) these events are as measured in the laboratory frame. Use the Lorentz transformation equation (L-10):
\[\Delta t=v \gamma \Delta x^{\prime}+\gamma \Delta t^{\prime} \nonumber \]
The relative velocity \(v_{\text {rel }}\) in equation \((\mathrm{L}-10)\) is just \(v\), the current speed of the rod. In the laboratory frame is the tap on the rear piece earlier or later than the tap on the front piece?
Your answer to part b predicts how much earlier the laboratory observer measures the tap to occur on the back piece than on the front piece of the rod. Let the tap increase the speed of the back end by \(d v\) as measured in the laboratory frame. Then during laboratory time \(\Delta t\) the back end is moving at a speed \(d v\) faster than the front end. This relative motion will shorten the distance between the back and front ends. After time interval \(\Delta t\) the front end receives the identical tap, also speeds up by \(d v\), and once again moves at the same speed as the back end.
c Show that the shortening \(d L\) predicted by this analysis is
\[\begin{aligned} d L &=-d v \Delta t=-\gamma \Delta x^{\prime} v d v=-v \gamma L_{\mathrm{o}} d v \\ &=-\frac{L_{\mathrm{o}} v d v}{\left(1-v^{2}\right)^{1 / 2}} \end{aligned} \nonumber \]
which is identical to the result of part \(\mathbf{a}\), which we wanted to explain. QED.
d Now start with the front and back pieces of the rod at rest in the laboratory frame and a distance \(L_{\text {o }}\) apart. Tap them repeatedly and identically. As they speed up, be sure these taps take place simultaneously in the rocket frame in which the two ends are currently at rest. (This requires you, the ride-along inspector, to resynchronize your rod-rest-frame clocks after each set of front-and-back taps.) Make a logically rigorous argument that after many taps, when the rod is moving at high speed relative to the laboratory, the length of the rod measured in the laboratory can be reckoned using the first equation given in this exercise.
- Now, by stages, put the rod back together. The full thousand pieces of the rod, lined up but not touching, are all tapped identically and at the same time in the current rest frame of the rod. One set of taps increases the rod’s speed from \(v\) to \(v+d v\) in the laboratory frame. Describe the time sequence of these thousand taps as observed in the laboratory frame. If you have studied Chapter 6 or the equivalent, answer the following questions: What kind of intervaltimelike, lightlike, or spacelike-separates any pair of the thousand taps in this set? Can this pair of taps be connected by a light flash? by a compression wave moving along the rod when the pieces are glued back together? Regarding the "logic of acceleration," is there any reason why we should not glue these pieces back together? Done!
f During the acceleration process is the reglued rod rigid - unchanging in dimensions - as observed in the rod frame? As observed in the laboratory frame? Is the rigidity property of an object an invariant, the same for all observers in uniform relative motion? Show how an ideal rigid rod could be used to transmit signals instantaneously from one place to another. What do you conclude about the idea of a "rigid body" when applied to high-speed phenomena?
Reference: Edwin F. Taylor and A. P. French, American Journal of Physics, Volume 51 , pages \(889-893\), especially the Appendix (1983).
11.9.15 the place where both agree
At any instant there is just one plane in which both the laboratory and the rocket clocks agree.
a By a symmetry argument, show that this plane lies perpendicular to the direction of relative motion. Using the Lorentz transformation equations, show that the velocity of this plane in the laboratory frame is equal to
\[v_{t=t^{\prime}}=\frac{1}{v_{\mathrm{rel}}}\left[1-\left(1-v_{\mathrm{rel}}^{2}\right)^{1 / 2}\right] \nonumber \]
b Does the expression for \(v_{t=t^{\prime}}\) seem strange? From our everyday experience we might expect that by symmetry the "plane of equal time" would move in the laboratory at half the speed of the rocket. Verify that indeed this is correct for the low relative velocities of our everyday experience. Use the first two terms of the binomial expansion
\[(1+z)^{n} \approx 1+n z \text { for }|z|<<1 \nonumber \]
to show that for low relative velocity, \(v_{t=t^{\prime}} \rightarrow v_{\text {rel }} / 2\).
c What is \(v_{t=t^{\prime}}\) for the extreme relativistic case in which \(v_{\text {rel }} \rightarrow 1\) ? Show that in this case \(v_{t=t^{\prime}}\) is completely different from \(v_{\text {rel }} / 2\).
d Suppose we want to go from the laboratory frame to the rocket frame in two equal velocity jumps. Try a first jump to the plane of equal laboratory and rocket times. Now symmetry does work: Viewed from this plane the laboratory and rocket frames move apart with equal and opposite velocities, whose magnitude is given by the equation in part a. A second and equal velocity jump should then carry us to the rocket frame at speed \(v_{\text {rel }}\) with respect to the laboratory. Verify this directly by using the Law of Addition of Velocities (Section 11.7) to show that
\[v_{\text {rel }}=\frac{v_{t=t^{\prime}}+v_{t=t^{\prime}}}{1+v_{t=t^{\prime}} v_{t=t^{\prime}}} \nonumber \]
11.9.16 Fizeau experiment
Light moves more slowly through a transparent material medium than through a vacuum. Let \(v_{\text {medium }}\) represent the reduced speed of light measured in the frame of the medium. Idealize to a case in which this reduced velocity is independent of the wavelength of the light. Place the medium at rest in a rocket moving at velocity \(v_{\text {rel }}\), to the right relative to the laboratory frame, and let light travel through the medium, also to the right. Use the Law of Addition of Velocities (Section L. 7) to find an expression for the velocity \(v\) of the light in the laboratory frame. Use the first two terms of the binomial expansion
\[(1+z)^{n} \approx 1+n z \text { for }|z|<<1 \nonumber \]
to show that for small relative velocity \(v_{\text {rel }}\) between the rocket and laboratory frames, the velocity \(v\) of the light with respect to the laboratory frame is given approximately by the expression
\[v \approx v_{\text {medium }}+v_{\text {rel }}\left(1-v_{\text {medium }}{ }^{2}\right) \nonumber \]
This expression has been tested by Fizeau using water flowing in opposite directions in the two arms of an interferometer similar (but not identical) to the interferometer used later by Michelson and Morley (Exercise 3-12).
Reference: H. Fizeau, Comptes rendus, Volume 33, pages 349-355 (1851). A fascinating discussion (in French) of some central themes in relativity theory - delivered more than fifty years before Einstein’s first relativity paper.

