4.2: E=mc²
- Page ID
- 3439
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Relativistic theory of gravity and \(E = mc^2\) explained
We now know the relativistic expression for kinetic energy in the limiting case of an ultrarelativistic particle: its energy is proportional to the “stretch factor” \(D\) of the Lorentz transformation. What about intermediate cases, like \(v = c/2\)?
When we are forced to tinker with a time-honored theory, our first instinct should always be to tinker as conservatively as possible. Although we’ve been forced to admit that kinetic energy doesn’t vary as \(v^2/2\) at relativistic speeds, the next most conservative thing we could do would be to assume that the only change necessary is to replace the factor of \(v^2/2\) in the nonrelativistic expression for kinetic energy with some other function, which would have to act like \(D\) or \(1/D\) for \(v \rightarrow \pm c\). I suspect that this is what Einstein thought when he completed his original paper on relativity in 1905, because it wasn’t until later that year that he published a second paper showing that this still wasn’t enough of a change to produce a working theory. We now know that there is something more that needs to be changed about prerelativistic physics, and this is the assumption that mass is only a property of material particles such as atoms (figure \(\PageIndex{1}\)). Call this the “atoms-only hypothesis.”
Now that we know the correct relativistic way of finding the energy of a ray of light, it turns out that we can use that to find what we were originally seeking, which was the energy of a material object. The following discussion closely follows Einstein’s.
Suppose that a material object \(O\) of mass \(m_o\), initially at rest in a certain frame \(A\), emits two rays of light (or any other kind of ultrarelativistic particles), each with energy \(E/2\). By conservation of energy, the object must have lost an amount of energy equal to \(E\). By symmetry, \(O\) remains at rest.
We now switch to a different frame of reference \(B\) moving at some arbitrary speed corresponding to a stretch factor \(D\). The change of frames means that we’re chasing one ray, so that its energy is scaled down to \(\left ( \frac{E}{2} \right )D^{-1}\), while running away from the other, whose energy gets boosted to \(\left ( \frac{E}{2} \right )D\). In frame \(B\), as in \(A\), \(O\) retains the same speed after emission of the light. But observers in frames \(A\) and \(B\) disagree on how much energy \(O\) has lost, the discrepancy being
\[E\left [ \frac{1}{2} (D + D^{-1})-1\right ]\]
This can be rewritten using identity [2] from section 3.6 as
\[E(\gamma -1)\]
Let’s consider the case where B’s velocity relative to A is small. Using the approximation \(\gamma \approx 1 + \frac{v^2}{2}\), our result is approximately
\[\frac{1}{2}Ev^2\]
neglecting terms of order \(v^4\) and higher. The interpretation is that when \(O\) reduced its energy by \(E\) in order to make the light rays, it reduced its mass from \(m_o\) to \(m_o - m\), where \(m = E\). Inserting the necessary factor of \(c^2\) to make this valid in units where \(c \neq 1\), we have Einstein’s famous
\[E = mc^2\]
This derivation entailed both an approximation and some hidden assumptions. These issues are explored more thoroughly in section 4.4. The result turns out to be valid for any isolated body.
We find that mass is not simply a built-in property of the particles that make up an object, with the object’s mass being the sum of the masses of its particles. Rather, mass and energy are equivalent, so that if the experiment of figure a is carried out with a sufficiently precise balance, the reading will drop because of the mass equivalent of the energy emitted as light.
The equation \(E = mc^2\) tells us how much energy is equivalent to how much mass: the conversion factor is the square of the speed of light, \(c\). Since \(c\) a big number, you get a really really big number when you multiply it by itself to get \(c^2\). This means that even a small amount of mass is equivalent to a very large amount of energy. Conversely, an ordinary amount of energy corresponds to an extremely small mass, and this is why nobody detected the non-null result of experiments like the one in figure \(\PageIndex{1}\) hundreds of years ago.
The big event here is mass-energy equivalence, but we can also harvest a result for the energy of a material particle moving at a certain speed. We have \(m(γ - 1)\) for the difference between \(O\)’s energy in frame \(B\) and its energy when it is at rest, i.e., its kinetic energy. But since mass and energy are equivalent, we assign \(O\) an energy m when it is at rest. The result is that the energy is
\[E = m\gamma\]
(or \(mγc^2\) in units with \(c \neq 1\)).
Example \(\PageIndex{1}\): Electron-positron annihilation
Natural radioactivity in the earth produces positrons, which are like electrons but have the opposite charge. A form of antimatter, positrons annihilate with electrons to produce gamma rays, a form of high-frequency light. Such a process would have been considered impossible before Einstein, because conservation of mass and energy were believed to be separate principles, and this process eliminates \(100\%\) of the original mass. The amount of energy produced by annihilating \(1\: kg\) of matter with \(1\: kg\) of antimatter is
\[\begin{align*} E&= mc^2\\ &= (2\: kg)\left ( 3.0 \times 10^8 m/s^2\right )^2 \\ &= 2 \times 10^{17}\: J \end{align*}\]
which is on the same order of magnitude as a day’s energy consumption for the entire world’s population!
Positron annihilation forms the basis for the medical imaging technique called a PET(positron emission tomography) scan, in which a positron-emitting chemical is injected into the patient and mapped by the emission of gamma rays from the parts of the body where it accumulates.

Example \(\PageIndex{2}\): A rusting nail
An iron nail is left in a cup of water until it turns entirely to rust. The energy released is about \(0.5\: MJ\). In theory, would a sufficiently precise scale register a change in mass? If so,how much?
Solution
The energy will appear as heat, which will be lost to the environment. The total mass-energy of the cup, water, and iron will indeed be lessened by \(0.5\: MJ\). (If it had been perfectly insulated, there would have been no change, since the heat energy would have been trapped in the cup.) The speed of light is \(c = 3×10^8\: m/s\), so converting to mass units, we have
\[\begin{align*} m&= \frac{E}{c^2}\\ &= \frac{0.5 \times 10^6\: J}{(3 \times 10^8\: m/s)^2}\\ &= 6 \times 10^{-12}\: kg \end{align*}\]
The change in mass is too small to measure with any practical technique. This is because the square of the speed of light is such a large number.
Example \(\PageIndex{3}\): Relativistic kinetic energy
By about 1930, particle accelerators had progressed to the point at which relativistic effects were routinely taken into account. In 1964, W. Bertozzi did a special-purpose experiment to test the predictions of relativity using an electron accelerator. The results were discussed in less detail in Example 3.3.1, at which point we had not yet seen the relativistic equation for kinetic energy. Electrons were accelerated through a static electric potential difference \(V\) to a variety of kinetic energies \(K = eV\), and their velocities inferred by measuring their time of flight through a beamline of length \(l = 8.4\: m\). Electrical pulses were recorded on an oscilloscope at the beginning and end of the time of flight \(t\). The energies were confirmed by calorimetry. Figure \(\PageIndex{3}\) shows a sample photograph of an oscilloscope trace at \(V = 1.5\: MeV\).
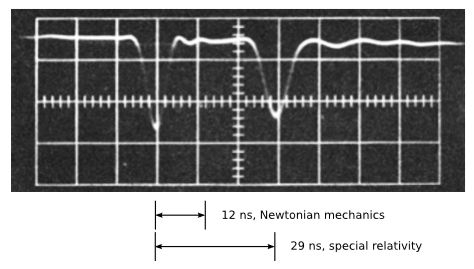
The prediction of Newtonian physics is as follows.
\[eV = \frac{1}{2}mv^2\]
\[\frac{v}{c} = 2.4\]
\[t = 12\: ns\]
According to special relativity, we have:
\[eV = m(\gamma -1)c^2\]
\[\frac{v}{c} = \sqrt{1 - \left ( 1 + \frac{eV}{mc^2} \right )^{-2}} = 0.97\]
\[t = 29\: ns\]
The results contradict the Newtonian prediction and are consistent with special relativity. According to Newton, this amount of energy should have accelerated the electrons to several times the speed of light. In reality, we see a clear demonstration of the nature of \(c\) as a limiting velocity.
Example \(\PageIndex{4}\): Gravity bending light

Gravity is a universal attraction between things that have mass, and since the energy in a beam of light is equivalent to some very small amount of mass, light should be affected by gravity, although the effect should be very small. The first experimental confirmation of relativity came in 1919 when stars next to the sun during a solar eclipse were observed to have shifted a little from their ordinary position. (If there was no eclipse, the glare of the sun would prevent the stars from being observed.) Starlight had been deflected by the sun’s gravity. The figure \(\PageIndex{4}\) is a photographic negative, so the circle that appears bright is actually the dark face of the moon, and the dark area is really the bright corona of the sun. The stars, marked by lines above and below then, appeared at positions slightly different than their normal ones.
Keep in mind that these arguments are very rough and qualitative,and it is not possible to produce a relativistic theory of gravity simply by taking \(E = mc^2\) and combining it with Newton’s law of gravity. After all, this law doesn’t refer to time at all: it predicts that gravitational forces propagate instantaneously. We know this can’t be consistent with relativity, which forbids cause and effect from propagating at any speed greater than \(c\). To produce a relativistic theory of gravity, we need general relativity.
Similar reasoning suggests that there may be stars—blackholes — so dense that their gravity can prevent light from leaving. Such stars have been detected, and their properties seem so far to be described correctly by general relativity.


