11.5: The Diesel Cycle
( \newcommand{\kernel}{\mathrm{null}\,}\)
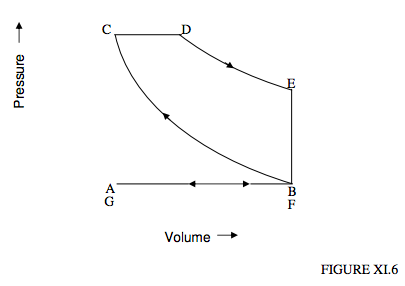
This difficulty is avoided in the Diesel cycle in that, during the adiabatic compression stage to a high temperature, it is just air (not an air-fuel mixture) that is compressed. Only then, when the temperature is high, is fuel injected, which then immediately ignites. The cycle is shown in figure XI.6.
We start at A. A valve opens and the piston moves back, and pure air (no fuel) is sucked into the cylinder. This is followed by an adiabatic compression from B to C, which can reach a high temperature of 2000 K or so. At C a jet of liquid fuel is forced at high pressure into the cylinder by a pump that is operated by the engine itself. The fuel immediately ignites. The rate of injection is held so that the mixture expands at constant pressure until we reach D, at which point the injection of fuel is cut off and the gas expands adiabatically to E. A valve is then opened so that the pressure drops to atmospheric at F. The piston then pushes the remainder of the mixture out, and the cycle stars anew.
It is left as an exercise to show:
Net work done by the engine per cycle = CP[TD−TB(PCPB)1−1/γ]−CV[TD(PBPCTpTB)γ−1−TB].
Volume of stroke = VB−VC=VB[1−(PBPC)1/γ].
Efficiency = 1−CV[TD(PBPCTDTB)γ−1−TB]CP[TD−TB(PCPB)1−1/γ].
Have a look at http://www.univ-lemans.fr/enseignements/physique/02/thermo/diesel.html
Exercise: Assuming γ = 1.4, what are the efficiencies of the Carnot, Otto and Diesel cycles running between 350 K and 2000 K? Assume for the Diesel cycle that the maximum pressure is 30 atmospheres. Assume for the Otto cycle that TC =650 K.


