16.2: The Third Law of Thermodynamics
- Page ID
- 7313
Nernst’s heat theorem and Planck’s extension of it, while originally derived from observing the behaviour of chemical reactions in solids and liquids, is now believed to apply quite generally to any processes, and, in view of that, it is time to reconsider our description of adiabatic demagnetization. We see immediately that figure XV.1 needs to be redrawn to reflect the fact that the entropy of the substance approaches zero whether or not it is situated in a magnetic field. The revised drawing is shown as figure XVI.1, in which I have drawn three consecutive magnetization-demagnetization operations, and it will be readily seen that we shall never reach a temperature of exactly zero in a finite number of operations.
The same applies to any operation in which we attempt to lower the temperature by a series of isothermal constraints that decrease the entropy followed by adiabatic relaxations – whether we are compressing a gas isothermally and then decompressing it adiabatically, or stretching a rubber band isothermally and loosening it adiabatically. In all cases, owing to the convergence of the two entropy curves at zero temperature, we are led to conclude:
It is impossible to reduce the temperature of a material body to the absolute zero of temperature in a finite number of operations.
This is the Third Law of Thermodynamics, and it is an inevitable consequence of Planck’s extension of Nernst’s Heat Theorem.
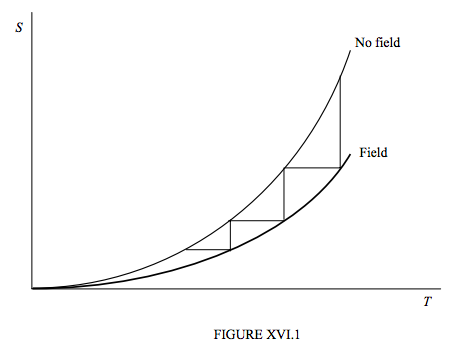
This is usually taken to mean that it is impossible ever to reduce the temperature of anything to absolute zero. From a practical point of view, that may be true, though that is not strictly what the third law says. It says that it is impossible to do it in a finite number of operations. I cannot help but think of a bouncing ball (see Classical Mechanics Chapter V), in which the ball bounces an infinite number of times before finally coming to rest after a finite time. After every bounce, there are still an infinite number of bounces yet to come, yet it is all over in a finite time. Now, perhaps some reader of these notes one day will devise a method of performing an infinite number of isothermal stress/adiabatic relaxation operations in a finite time, and so attain absolute zero.
The third law also talks about a finite number of operations – by which I take it is meant operations such as an entropy-reducing constraint followed by an adiabatic relaxation. I am not sure to what extent this applies to processes such as laser cooling. In such experiments a laser beam is directed opposite to an atomic beam. The laser frequency is exactly equal to the frequency need to excite the atoms to their lowest excited level, and so it stops the atoms in their tracks. As the atoms slow down, the required frequency can be changed to allow for the Doppler effect. Such experiments have reduced the temperature to a fraction of a nanokelvin. These experiments do not seem to be of the sort of experiment we had in mind when developing the third law of thermodynamics. We might well ask ourselves if it is conceptually possible or impossible to reduce the speeds of a collection of atoms to zero for a finite period of time. We might argue that it is conceptually possible – but then we may remember that atoms attract each other (van der Waals forces), so, if all the atoms are instantaneously at rest, they will not remain so. Of course if we had an ideal gas (such as a real gas extrapolated to zero pressure!) such that there are no forces between the molecules, the concept of zero temperature implies that all the atoms are stationary – i.e. each has a definite position and zero momentum. This is, according the Heisenberg’s uncertainty principle, inconceivable. So I leave it open as a subject for lunchtime conversations exactly how strictly the third law prevents us from ever attaining the absolute zero of temperature.
Exercise. If the kinetic temperature of a set of hydrogen atoms is reduced to a tenth of a nanokelvin, what is the root-mean-square speed of the atoms?


