1.3: Equation of State

The Ideal Gas Equation of State

In specifying the equation of state, we will use the absolute temperature, denoted by \(t\). We will introduce this concept later, but for now, we will take it as given. The absolute temperature is always positive, varying from zero (or absolute zero) to infinity. The ideal gas is then characterized by the equation of state

\[p\,V=n\,k\,T\]

where \(N\) denotes the number of molecules of the gas and \(k\) is a constant, known as Boltzmann’s constant. Another way of writing this is as follows. We define the Avogadro number as \(6.02214 \times 10^{23}\). This number comes about as follows. The mass of an atom is primarily due to the protons and neutrons in its nucleus. Each proton has a mass of \(1.6726×10^{−24} gm\), each neutron has a mass of \(1.6749×10^{−24} gm\). If we neglect the mass difference between the proton and the neutron, the mass of an atom of atomic weight \(A\) (= number of protons + number of neutrons in the nucleus) is given by \(A \times 1.6726 \times 10^{−24} gm\). Thus if we take \(A\) grams of the material, the number of atoms is given by \((1.67 \times 10^{−24})^{−1} ≈ 6 × 10^{23}\). This is essentially the Avogadro number. The mass difference between the proton and neutron is not completely negligible and also there are slight variations from one type of nucleus to another due to the varying binding energies of the protons and neutrons. So we standardize the Avogadro number by defining it as \(6.02214 \times 10^{23}\), which is very close to the number of atoms in \(12\, gm\) of the isotope \(C^{12}\) of carbon (which was used to standardize the atomic masses).

If we have \(N\) molecules of a material, we say that it has\(n\) moles of the material, where \(n = \frac{N}{\text{Avogadro Number}}\). Thus we can rewrite the ideal gas equation of state as

\[p\,V=n\,R\,T, \quad R=k\,(\text{Avogadro Number})\]

Numerically, we have, in joules per kelvin unit of temperature,

\[k≈1.38065 \times 10^{-23}\,\frac{J}{K} , \quad R≈8.3145\,\frac{J}{\text{mole}\;K}\]

The van der Waals Equation of State

The ideal gas law is never obtained for real gases. There are intermolecular forces which change the equation of state, not to mention the quantum nature of the dynamics of the molecules which becomes more important at low temperatures. The equation of state can in principle be calculated or determined from the intermolecular forces in statistical mechanics. The corrections to the ideal gas law can be expressed as series of terms known as the virial expansion, the second virial coefficient being the first such correction. While the method is general, the specifics depend on the nature of the molecules and a simple formula is not easy to write down.

Figure \(\PageIndex{1}\): The general form of the intermolecular potential as a function of distance

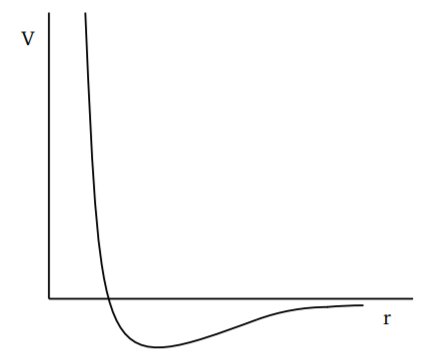
An equation of state which captures some very general features of the intermolecular forces was written down by van der Waals, in the 1870s, long before the virial expansion was developed. It is important in that it gives a good working approximation for many gases. The van der Waals equation of state is

\[(p + \frac{aN^2}{V^2})(V − bN) = NkT \label{1.3.4}\]

The reasoning behind this equation is as follows. In general, intermolecular forces have a short range repulsion, see Fig. 1.3.1. This prevents the molecules from forming bound states. The formation of bound states would be a chemical reaction, so we are really considering gases where there is no further chemical reaction beyond the initial formation of the molecules. For example, if we consider oxygen, two oxygen atoms bind together to form the oxygen molecule \(O_2\), but there is no binding for two oxygen molecules (two \(O_2\)’s) to form something more complicated. At the potential level, this is due to a short range repulsion keeping them from binding together. In van der Waals’ reasoning, such an effect could be incorporated by arguing that the full volume \(V\) is not available to the molecules, a certain volume \(b\) around each molecule is excluded from being accessible to other molecules. So we must replace \(V\) by \((V − bN)\) in the ideal gas law.

Intermolecular forces also have an attractive part at slightly larger separations. This attraction would lead to the molecules coming together, thus reducing the pressure. So the pressure calculated assuming the molecules are noninteracting, which is the kinetic pressure \(p_{kin}\), must be related to the actual pressure \(p\) by

\[p=p_{kin}−\frac{aN^2}{V^2} \label{1.3.5}\]

The interaction is pairwise primarily, so we expect a factor of \(\frac{N(N − 1)}{2}\) (which is number of pairings one can do) for \(N\) molecules. This goes like ∼\(N^2\), which explains the second term in Equation \ref{1.3.5}. Using the ideal gas law for \(p_{\text{kin}}\) with the volume \((V − bN)\), we get Equation \ref{1.3.4}. In this equation, \(a\) and \(b\) are parameters specific to the gas under consideration.