9.2: Carathéodory Statement of the Second Law
- Page ID
- 32049
The statement of the second law due to Carathéodory is:
Definition: Carathéodory Principle
In the neighborhood of any equilibrium state of a physical system with any number of thermodynamic coordinates, there exist states which are inaccessible by adiabatic processes.
The adiabatic processes can be quite general, not necessarily quasi-static. It is easy to see that this leads immediately to the notion of absolute temperature and entropy. This has been discussed in a concise and elegant manner in Chandrasekhar’s book on stellar structure. We briefly repeat his argument for completeness. For simplicity, consider a gas characterized by pressure \(p\) and volume \(V\), and (empirical) temperature \(t\), only two of which are adequate to specify the thermodynamic state, the third being given by an equation of state. Since these are the only variables, \(dQ\) has an integrating factor and we may write
\[ dQ = τ dσ \label{9.2.1}\]
where \(σ\) and \(τ\) will be functions of the variables \(p, V, t\). The power of Carathéodory’s formulation becomes clear when we consider two such systems brought into thermal contact and come to equilibrium. We then have a common temperature t and the thermodynamic variables can now be taken as \(V_1, V_2, t\) (or \(t\) and one variable from each of \((p_1, V_1), (p_2, V_2))\). We also have \(dQ = dQ_1 + dQ_2\). The number of variables is now three; nevertheless, the Carathéodory principle tells us that we can write
\[ τ d_σ = τ_1 dσ_1 + τ_2 dσ_2 \label{9.2.2}\]
We now choose \(t, σ_1, σ_2\) as the independent variables. Equation \ref{9.2.2} then leads to
\[\frac{∂σ}{∂σ_1} = \frac{τ_1}{τ},\;\;\;\;\;\; \frac{∂σ}{∂σ_2} = \frac{τ_2}{τ},\;\;\;\;\;\; frac{∂σ}{∂t} = 0 \label{9.2.3} \]
The last of these equations tells us that \(σ\) is only a function of \(σ_1\) and \(σ_2\), \(σ = σ(σ_1, σ_2)\). Further, since σ is a well-defined function of the various variables, derivatives on \(σ\) commute and so
\[ \frac{∂}{∂t} \frac{∂σ}{∂σ_1} - \frac{∂σ}{∂σ_1} \frac{∂σ}{∂t} = 0 \label{9.2.4}\]
with a similar relation for derivatives with respect to \(σ_2\) as well. Thus we have the result
\[ \frac{∂}{∂t} \left( \frac{τ_1}{τ} \right) = 0,\;\;\;\;\;\; \frac{∂}{∂t} \left( \frac{τ_2}{τ} \right) = 0 \label{9.2.5}\]
Equivalently, we can write
\[ \frac{1}{τ_1} \frac{∂τ_1}{∂t} = \frac{1}{τ_2} \frac{∂τ_2}{∂t} = \frac{1}{τ} \frac{∂τ}{∂t} \label{9.2.6} \]
This shows that the combination \( \left( \frac{1}{τ} \right) \left( \frac{∂τ}{∂t} \right) \) is independent of the system and is a universal function of the common variable \(t\). Taking this function as \(g(t)\) and integrating, we get
\[ \begin{equation}
\begin{split}
τ & = Σ (σ_1, σ_2) C \text{ exp} \left( \int_{t_0}^t dt\;g(t) \right) \\[0.125in] τ_1 & = Σ_1 (σ_1) C \text{ exp} \left( \int_{t_0}^t dt\;g(t) \right) \\[0.125in]
τ_2 & =Σ_2 (σ_2) C \text{ exp} \left( \int_{t_0}^t dt\;g(t) \right)
\end{split}
\end{equation} \label{9.2.7} \]
The \(τ\)’s are determined up to a function of the \(σ\)’s; we take this arbitrariness as \(C Σ \), where \(C\) is a constant and \( Σ \) is a function of the \(σ\)’s involved. We can now define the absolute temperature as
\[ T ≡ C \text{ exp} \left( \int_{t_0}^t dt\;g(t) \right) \label{9.2.8} \]
Notice that, in the case under consideration, \(T_1 = T_2 = T\) as expected for equilibrium. This gives \(dQ_1 = T Σ_1dσ_1\), etc. The relation \(dQ = dQ_1 + dQ_2\) now reduces to
\[ Σ dσ = Σ_1 dσ_1 + Σ_2 dσ_2 \label{9.2.9} \]
In the two-dimensional space with coordinates \(σ_1\), \(σ_2\), the vector \((Σ_1, Σ_2)\) has vanishing curl, i.e., \(∂_1Σ_2 − ∂_2Σ_1 = 0\), since \(Σ_1\) only depends on \(σ_1\) and similarly for \(Σ_2\). Thus Equation \ref{9.2.9} shows that \(Σd_σ\) is a perfect differential. This means that there exists a function \(S\) such that \(Σd_σ = dS\); this also means that \(Σ\) can depend on \(σ_1\) and \(σ_2\) only through the combination \(σ(σ_1, σ_2)\). Thus finally we have
\[dQ = T\;dS \]
In this way, the Carathéodory principle leads to the definition of entropy \(S\).
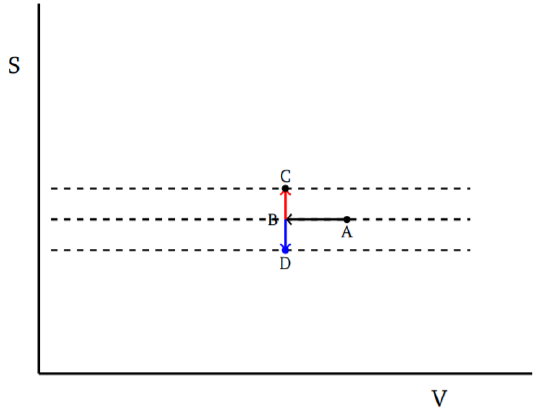
One can also see how this leads to the principle of increase of entropy. For this, consider a system with \(n\) thermodynamic variables. The entropy will be a function of these. We can alternatively choose \(n − 1\) of the given variables and the entropy \(S\) to characterize states of the system. Now we ask the question: Given a state \(A\), can we find a path which takes us via adiabatic processes to another state \(C\)? It is useful to visualize this in a diagram, with \(S\) as one of the axes, as in Fig. 9.2.1. We show one of the other axes, but there could be many. To get to \(C\), we can start from \(A\) and go along a quasi-static reversible adiabatic to \(B\) and then, via some nonquasi-static process such as stirring, mixing, etc., get to \(C\), keeping the system in adiabatic isolation. This second process can be irreversible. The idea is that the first part does not change the entropy, but brings the other variables to their desired final value. Then we move to the required value of \(S\) by some irreversible process. As shown \(SC > SB = SA\). Suppose the second process can also decrease the entropy in some cases so that we can go from \(B\) to \(D\) by some similar process. Then we see that all states close to \(B\) are accessible. Starting from any point, we can move along the surface of constant \(S\) to get to the desired value of the variables, except for \(S\) and then jump to the required value of \(S\) by the second process. This contradicts the Carathéodory principle. Thus, if we postulate this principle, then we have to conclude that in all irreversible processes in adiabatic isolation the entropy has to either decrease or increase; we cannot have it increase in some processes and decrease in some other processes. So \(S\) should be either a nondecreasing quantity or a nonincreasing quantity. The choice of the sign of the absolute temperature, via the choice of the sign of the constant \(C\) in Equation \ref{9.2.8}, is related to which case we choose for entropy. The conventional choice, of course, is to take \(T ≥ 0\) and entropy to be nondecreasing. In other words
\[ ∆S ≥ 0 \]
Thus effectively, we have obtained the version of the second law as given in Proposition 4 in Chapter 3.