4.3: Thermal Conductivity
( \newcommand{\kernel}{\mathrm{null}\,}\)
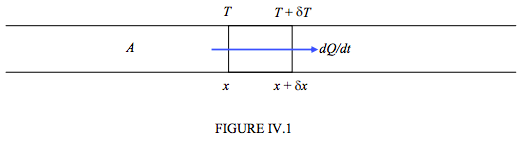
Figure IV.1 shows heat flowing at a rate dQ/dt along a bar of cross-sectional area A of material. There is a temperature gradient along the length of the bar (which is why heat is flowing down it). At a distance x from the end of the bar the temperature is T; at a distance x + δx it is T + δT. Note that, if heat is flowing in the positive direction as shown, δT must be negative. That is, it is cooler towards the right hand end of the bar. The temperature gradient dT/dx is negative. Heat flows in the opposite direction to the temperature gradient.
The ratio of the rate of heat flow per unit area to the negative of the temperature gradient is called the thermal conductivity of the material:
dQdt=−KAdTdx.
I am using the symbol K for thermal conductivity. Other symbols often seen are k or λ. Its SI unit is W m−1K−1.
I have defined it in a one-dimensional situation and for an isotropic medium, in which case the heat flow is opposite to the temperature gradient. One can imagine that, in an anisotropic medium, the rate of heat flow and the temperature gradient may be different parallel to the different crystallographic axes. In that case the heat flow and the temperature gradient may not be strictly antiparallel, and the thermal conductivity is a tensor quantity. Such a situation will not concern us in this chapter.
If, in our one-dimensional example, there is no escape of heat from the sides of the bar, then the rate of flow of heat along the bar must be the same all along the bar, which means that the temperature gradient is uniform along the length of the wire. It may be easier to imagine no heat loss from the sides than to achieve it in practice. If the bar were situated in a vacuum, there would be no loss by conduction or convection, and if the bar were very shiny, there would be little loss by radiation.
Order-of-magnitude values of the thermal conductivities of common substances are
Air 0.03 W m−1K−1
Water 0.6
Glass 0.8
Fe 80
Al 240
Cu 400
It is easy to imagine how heat may be conducted along a solid, with the vibrations of the atoms at one end of the solid being transmitted to the next atoms by one atom nudging the next, and so on. However, it is evident from the table, and in any case is common knowledge, that some substances (metals) conduct heat much better than others. Indeed, among the metals, there is a close correlation between the thermal and electrical conductivities (at a given temperature). This suggests that the mechanism for thermal conductivity in metals is the same as for electrical conductivity. Heat is conducted in a metal primarily by electrons.
It would be an interesting exercise to find, from the Web or from other references, the thermal and electrical conductivities of a number of metals. It may be found that thermal conductivities, K, are sometimes quoted in unfamiliar “practical” units, such as BTU per hour per square foot for a temperature gradient of 1 F° per inch, and converting these to SI units of W m−1K−1 might be a bit of a challenge. Electrical conductivities, σ, decrease somewhat with rising temperature (so do thermal conductivities, but rather less so), so it would be important to find them all at the same temperature. Then you could see whether the ratio K/σ is indeed the same for all metals at a given temperature. This is known as the Wiedemann-Franz Law. First-order theory (which we do not give here) predicts that
KσT=13(πke)2=2.44×10−8WΩK−1.
Here k is Boltzmann’s constant and e is the electronic charge. This prediction is found to be obeyed well at room temperatures and higher, but at low temperatures the electrical conductivity increases rapidly with lowering temperature, and the ratio starts to fall well below the value predicted by equation 4.2.2, approaching zero at 0 K.
The reader may be familiar with the following terms in electricity
Conductivity σ
Conductance G
Resistivity ρ
Resistance R
They are related by G = 1/R, σ = 1/ρ, R = ρl/A, G = σA/l,
where l and A are the length and cross-sectional area of the conductor. The reader probably also knows that resistances add in series and conductances add in parallel. We may define some analagous quantities related to heat flow. Thus resistivity is the reciprocal of conductivity, resistance is l/A times resistivity, conductance is A/l times conductivity, and so on. These concepts may come in useful in the following genre of problems beloved of examiners.
A room has walls of area A1, thickness d1, thermal conductivity K1, a door of area A2, thickness d2, thermal conductivity K2, and a window of area A3, thickness d3, thermal conductivity K3, The temperature inside is T1 and the temperature outside is T2. What is the rate of heat loss from the room?
We have three conductances in parallel: K1A1d1, K2A2d2,, and K3A3d3, and so we have
dQdt=(K1A1d1+K2A2d2+K3A3d3)(T2−T1).
Of course, the problem need not be exactly like that. Perhaps you are given the rate of heat loss and asked to find the area of the window. But you get the general idea, and you can probably concoct a few examples yourself. The rate of heat flow is analogous to the current, and the temperature difference is like the EMF of a battery.


