6.6: Collisions
- Page ID
- 7247
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section, we are going to ask: What is the mean time between intermolecular collisions? What is the mean free path between collisions? How many intermolecular collisions are there per unit volume per unit time? How many collisions with the walls of a containing vessel are there per unit area per unit time? Since I know little chemistry, I shall assume that molecules are hard spheres of diameter d. This may not be too bad for monatomic gases such as the rare gases. For others, the assumption is tantamount to assuming that molecules repel each other when their centres of mass approach within a distance d. In any case, we shall assume that the collision cross-section is of area πd2.
Notice, from the sketch below, that two equal spheres collide when their centres are separated by their diameter d, and consequently the collision cross section (shown as a dashed circle) is of area πd2.
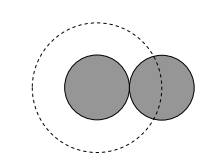
In fact in what follows, I’m just going to call the area of the collision cross section σ; in doing that, I don’t even have to assume that its shape is circular.
In time t, a molecule moving with speed c sweeps out a cylinder of volume σct. If there are n molecules per unit volume, the number of collisions that that particular molecule will experience in time t would appear to be σctn, which is to say that the number of collisions it experiences in unit time is σcn. Thus the mean time τ between collisions would appear to be ), τ = 1/(σcn) and the mean free path λ between collisions is ). λ = 1/(σn).
But this isn't quite right, because we have not taken into account the fact that all the molecules in the above-mentioned cylinder are moving. It is not as though our hero molecule were colliding with a set of stationary molecules. The relevant speed to use in this analysis is the mean relative speed between molecules, and this is a little greater than the speed c of each. Let’s see if we can do a little better.
Let’s start by supposing that all of the molecules are moving with speed c. There are two extreme sorts of collision:
The “head on” collision:
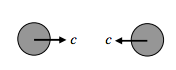
For such a collision, the relative speed between the molecules is 2c.
Then there is the sort of collision in which one molecule barely catches up with another one:
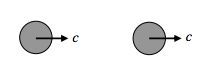
In that case the relative speed is zero.
The average relative speed is evidently somewhere between 0 and 2c.
These are extreme cases. The “average” situation is somewhat in between. We may argue that the “average” situation is for the two molecules to be travelling in perpendicular paths:
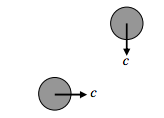
If we think of this as the “average” situation, then we may argue that the “average” relative speed between two molecules is \( \sqrt{2} c\). In that case, we may conclude that the mean time between collisions is \( \tau=1 /(\sqrt{2} \sigma c n)\), and the mean free path is \( \lambda=1 /(\sqrt{2} \sigma n)\).
This argument may or may not be completely convincing, but it is probably closer to the mark than our previous effort.
Let’s see if we can make a further improvement. As before, we’ll suppose that each molecule is moving with speed c.
Suppose our hero molecule to be moving upward with speed c, and another molecule approaches at an angle θ, as in the sketch below.
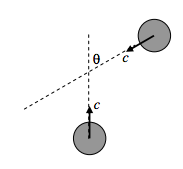
By vector addition of velocities, it will be seen (a little thought will be needed) that the relative speed of approach between the two molecules is \( \sqrt{2} c(1+\cos \theta)^{1 / 2}\).
Now the fraction of molecules approaching from angles between θ and θ + dθ is \( \frac{1}{2} \sin \theta d \theta\). This is because the area of an elemental zone of a sphere of unit radius between θ and θ + dθ is 2πsinθdθ, and the total area of the sphere is 4π - see the sketch below:
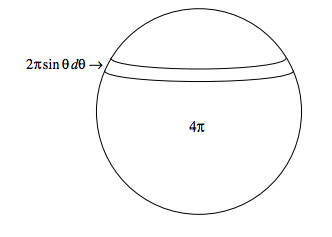
Thus the mean relative speed of all the molecules is \( \int_{0}^{\pi} \sqrt{2} c(1+\cos \theta)^{1 / 2} \times \frac{1}{2} \sin \theta d \theta \), which works out to be \( \frac{4}{3} c\).
In this model, then, the mean time between collisions would be \( \tau=\frac{1}{\frac{4}{3} \sigma c n}\), and the mean free path would be \( \lambda=\frac{1}{\frac{4}{3} \sigma n}\).
However, we have still assumed that all the molecules are moving at the same speed. I am told (but I have not verified it myself) that, if you take account of the Maxwell-Boltzmann distribution of speeds (see Section 6.7), the mean relative speed of collision is \( \sqrt{2} \overline{c}\), where \( \overline{c}\) is the mean speed of the Maxwell-Boltzmann distribution (equal to \( \sqrt{\frac{8 k T}{\pi m}}\).) If that is so, then we obtain \( \tau=\frac{1}{\sqrt{2} \sigma \overline{c} n} \quad\) and \( \quad \lambda=\frac{1}{\sqrt{2} \sigma n}\).
In any case, since molecules are not hard spheres (they are neither spheres nor hard) and the details of a “collision” depend on the shape of the molecules and the force law between them, it may not be meaningful to try to obtain an extremely precise formula for the mean free path, but instead settle for \( \tau=\frac{1}{b \sigma \overline{c} n}\) and \( \lambda=\frac{1}{b \sigma n}\), and if you wish to take \( b \approx \sqrt{2}\), you won’t be far out.
Of more interest would be to calculate the mean time between collisions for various pressures and temperatures, and ask how does this compare, for example, with the mean lifetime of an atom in an excited atomic level, or a metastable level. Or to compare the mean free path between collisions with the mean nearest-neighbour distance between molecules in a gas. I think under typical familiar conditions, you’ll find that the mean free path is rather longer than the mean nearest-neighbour distance.
Also of interest is the number of collisions per unit volume per unit time. If we suppose that a single molecule experiences \(b \sigma \overline{c} n\) collisions per unit time, and there are n molecules per unit volume, then the number of collisions per unit volume per unit time is
\(Z=\frac{1}{2} b \sigma \overline{c} n^{2}\).
The factor of \( \frac{1}{2}\) is necessary so that we don’t count collisions of A with B and of B with A as two different collisions.
Another useful result is that the number of molecules striking the walls of a containing vessel per unit area per unit time is
\( \frac{1}{4} n \overline{c}\)
To avoid repetition, I don't derive this here, but you will find a derivation in Chapter 1 Section 1.17 of Stellar Atmospheres, where I do the derivation with photons rather than with molecules. The only difference is that, in the case of the photons, all are moving at the same speed c (the speed of light), whereas here we have a distribution of speeds, and we use \(\overline{c}\), the mean speed of the molecules.


