17.8: Entropy of Mixing, and Gibbs' Paradox
( \newcommand{\kernel}{\mathrm{null}\,}\)
In Chapter 7, we defined the increase of entropy of a system by supposing that an infinitesimal quantity dQ of heat is added to it at temperature T, and that no irreversible work is done on the system. We then asserted that the increase of entropy of the system is dS = dQ/T. If some irreversible work is done, this has to be added to the dQ.
We also pointed out that, in an isolated system any spontaneous transfer of heat from one part to another part was likely (very likely!) to be from a hot region to a cooler region, and that this was likely (very likely!) to result in an increase of entropy of the closed system − indeed of the Universe. We considered a box divided into two parts, with a hot gas in one and a cooler gas in the other, and we discussed what was likely (very likely!) to happen if the wall between the parts were to be removed. We considered also the situation in which the wall were to separate two gases consisting or red molecules and blue molecules. The two situations seem to be very similar. A flow of heat is not the flow of an “imponderable fluid” called “caloric”. Rather it is the mixing of two groups of molecules with initially different characteristics (“fast” and “slow”, or “hot” and “cold”). In either case there is likely (very likely!) to be a spontaneous mixing, or increasing randomness, or increasing disorder or increasing entropy. Seen thus, entropy is seen as a measure of the degree of disorder. In this section we are going to calculate the increase on entropy when two different sorts of molecules become mixed, without any reference to the flow of heat. This concept of entropy as a measure of disorder will become increasingly apparent if you undertake a study of statistical mechanics.
Consider a box containing two gases, separated by a partition. The pressure and temperature are the same in both compartments. The left hand compartment contains N1 moles of gas 1, and the right hand compartment contains N2 moles of gas 2. The Gibbs function for the system is
G=RT[N1(lnP+ϕ1)+N2(lnP+ϕ2)].
Now remove the partition, and wait until the gases become completely mixed, with no change in pressure or temperature. The partial molar Gibbs function of gas 1 is
μ1=RT(lnp1+ϕ1)
and the partial molar Gibbs function of gas 2 is
μ2=RT(lnp2+ϕ2).
Here the pi are the partial pressures of the two gases, given by and p1 = n1P, p2 = n2P where the ni are the mole fractions.
The total Gibbs function is now N1µ1 + N2µ2, or
G=RT[N1(lnn1+lnP+ϕ1)+N2(lnn2+lnP+ϕ2)].
The new Gibbs function minus the original Gibbs function is therefore
ΔG=RT(N1lnn1+N2lnn2)=NRT(n1lnn1+n2lnn2).
This represents a decrease in the Gibbs function, because the mole fractions are less than 1.
The new entropy minus the original entropy is ΔS=−[∂(ΔG)∂T]P, which is
ΔS=−NR(n1lnn1+n2lnn2).
This is positive, because the mole fractions are less than 1.
Similar expressions will be obtained for the increase in entropy if we mix several gases.
Here’s maybe an easier way of looking at the same thing. (Remember that, in what follows, the mixing is presumed to be ideal and the temperature and pressure are constant throughout.)
Here is the box separated by a partition:

Concentrate your attention entirely upon the left hand gas. Remove the partition. In the first nanosecond, the left hand gas expands to increase its volume by dV, its internal energy remaining unchanged (dU = 0). The entropy of the left hand gas therefore increases according to dS=PdVT=N1RdVV. By the time it has expanded to fill the whole box, its entropy has increased by ln( / ). RN1 ln(V/V1). Likewise, the entropy of the right hand gas, in expanding from volume V2 to V, has increased by RN2 ln(V/V2). Thus the entropy of the system has increased by R[ N1 ln(V/V1) ln(V/V2)], and this is equal to RN[ n1 ln(1/n1) ln(1/n2)] = − NR[n1 ln n1 + n2 ln n2].
Where there are just two gases, n2 = 1 − n1, so we can conveniently plot a graph of the increase in the entropy versus mole fraction of gas 1, and we see, unsurprisingly, that the entropy of mixing is greatest when n1=n2=12, when ∆S = NR ln 2 = 0.6931NR.
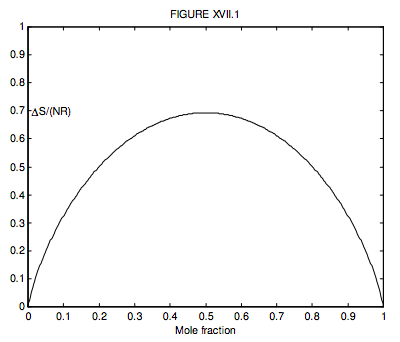
What is n1 if ΔS=12NR? (I make it n1 = 0.199 710 or, of course, 0.800 290.)
We initially introduced the idea of entropy in Chapter 7 by saying that if a quantity of heat dQ is added to a system at temperature T, the entropy increases by dS = dQ/T. We later modified this by pointing out that if, in addition to adding heat, we did some irreversible work on the system, that irreversible work was in any case degraded to heat, so that the increase in entropy was then dS = (dQ + dWirr)/T. We now see that the simple act of mixing two or more gases at constant temperature results in an increase in entropy. The same applies to mixing any substances, not just gases, although the formula −NR[n1 ln n1 + n2 ln n2] applies of course just to ideal gases. We alluded to this in Chapter 7, but we have now placed it on a quantitative basis. As time progresses, two separate gases placed together will spontaneously and probably (very probably!) irreversibly mix, and the entropy will increase. It is most unlikely that a mixture of two gases will spontaneously separate and thus decrease the entropy.
Gibbs’ Paradox arises when the two gases are identical. The above analysis does nothing to distinguish between the mixing of two different gases and the mixing of two identical gases. If you have two identical gases at the same temperature and pressure in the two compartments, nothing changes when the partition is removed – so there should be no change in the entropy. Within the confines of classical thermodynamics, this remains a paradox – which is resolved in the study of statistical mechanics.
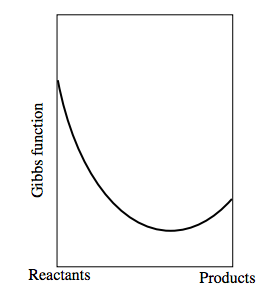
Now consider a reversible chemical reaction of the form Reactants ↔ Products − and it doesn’t matter which we choose to call the “reactants” and which the “products”. Let us suppose that the Gibbs function of a mixture consisting entirely of “reactants” and no “products” is less than the Gibbs function of a mixture consisting entirely of “products”. The Gibbs function of a mixture of reactants and products will be less than the Gibbs function of either reactants alone or products alone. Indeed, as we go from reactants alone to products alone, the Gibbs function will look something like this:
The left hand side shows the Gibbs function of the reactants alone. The right hand side shows the Gibbs function for the products alone. The equilibrium situation occurs where the Gibbs function is a minimum.
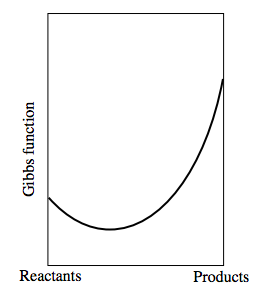
If the Gibbs function of the reactants were greater than that of the products, the graph would look something like: